Aufgabe 2B
Ein Unternehmen produziert Stahlkugeln für Kugellager. Erfahrungsgemäß sind 4 % aller fehlerhaft.
800 Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.
Alle Kugeln werden vor dem Verpacken geprüft. Dabei werden 95 % der Kugeln mit Formfehler, 98 % der Kugeln mit Größenfehler, aber auch 0,5 % der Kugeln ohne Fehler aussortiert.
800 Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.
a)
Bestimme die Wahrscheinlichkeit dafür, dass unter den ausgewählten Kugeln weniger als 30 fehlerhaft sind.
(2 BE)
b)
Bestimme die Wahrscheinlichkeit dafür, dass die Anzahl der fehlerhaften Kugeln unter den ausgewählten höchstens um eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht.
Eine Stahlkugel hat entweder keinen Fehler, einen Formfehler oder einen Größenfehler. Die Wahrscheinlichkeit für einen Formfehler beträgt 3 % die für einen Größenfehler 1 %.
(5 BE)
Alle Kugeln werden vor dem Verpacken geprüft. Dabei werden 95 % der Kugeln mit Formfehler, 98 % der Kugeln mit Größenfehler, aber auch 0,5 % der Kugeln ohne Fehler aussortiert.
c)
Stelle den Sachzusammenhang in einem beschrifteten Baumdiagramm dar.
(4 BE)
d)
Gib das Ergebnis des folgenden Terms an und interpretiere die Bedeutung des Ergebnisses im Sachzusammenhang:
(3 BE)
e)
Berechne die Wahrscheinlichkeit dafür, dass eine aussortierte Kugel keinen Formfehler hat.
(3 BE)
f)
Bei Stahlkugeln, die während der ersten Überprüfung nicht aussortiert wurden, wird die Überprüfung aus Sicherheitsgründen ein weiteres Mal durchgeführt.
Berechne die Wahrscheinlichkeit dafür, dass eine bei der zweiten Überprüfung aussortierte Kugel keinen Fehler aufweist.
Berechne die Wahrscheinlichkeit dafür, dass eine bei der zweiten Überprüfung aussortierte Kugel keinen Fehler aufweist.
(4 BE)
g)
Die Kugeln werden in Packungen verkauft. Ein Teil der verkauften Packungen wird zurückgegeben. Die Wahrscheinlichkeit dafür, dass eine verkaufte Packung zurückgegeben wird, beträgt 3 %. Dem Unternehmen entsteht pro Packung, die zurückgegeben wird, ein Verlust von 5,80 Euro. Pro Packung, die nicht zurückgegeben wird, erzielt das Unternehmen einen Gewinn von 8,30 Euro.
Bestimme die Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von 200 Packungen einen Gesamtgewinn von mindestens 1500 Euro erzielt.
Bestimme die Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von 200 Packungen einen Gesamtgewinn von mindestens 1500 Euro erzielt.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Die Zufallsvariable 
beschreibt die Anzahl der fehlerhaften Kugeln.
ist 
verteilt.
Die gesuchte Wahrscheinlichkeit beträgt ungefähr 
b)
Der Erwartungswert beträgt 
Die halbe Standardabweichung lässt sich berechnen durch
Die untere Grenze des Bereich, in dem die Anzahl der fehlerhaften Kugeln höchstens um diesen Wert vom Erwartungswert abweicht, ist gegeben durch die kleinste natürliche Zahl, die größer als 
ist, also 
Die obere Grenze dieses Bereichs ist gegeben durch die größte natürliche Zahl, die kleiner als
ist, also 
Schließlich gilt 
Die gesuchte Wahrscheinlichkeit beträgt ungefähr 
Die halbe Standardabweichung lässt sich berechnen durch
Die obere Grenze dieses Bereichs ist gegeben durch die größte natürliche Zahl, die kleiner als
c)
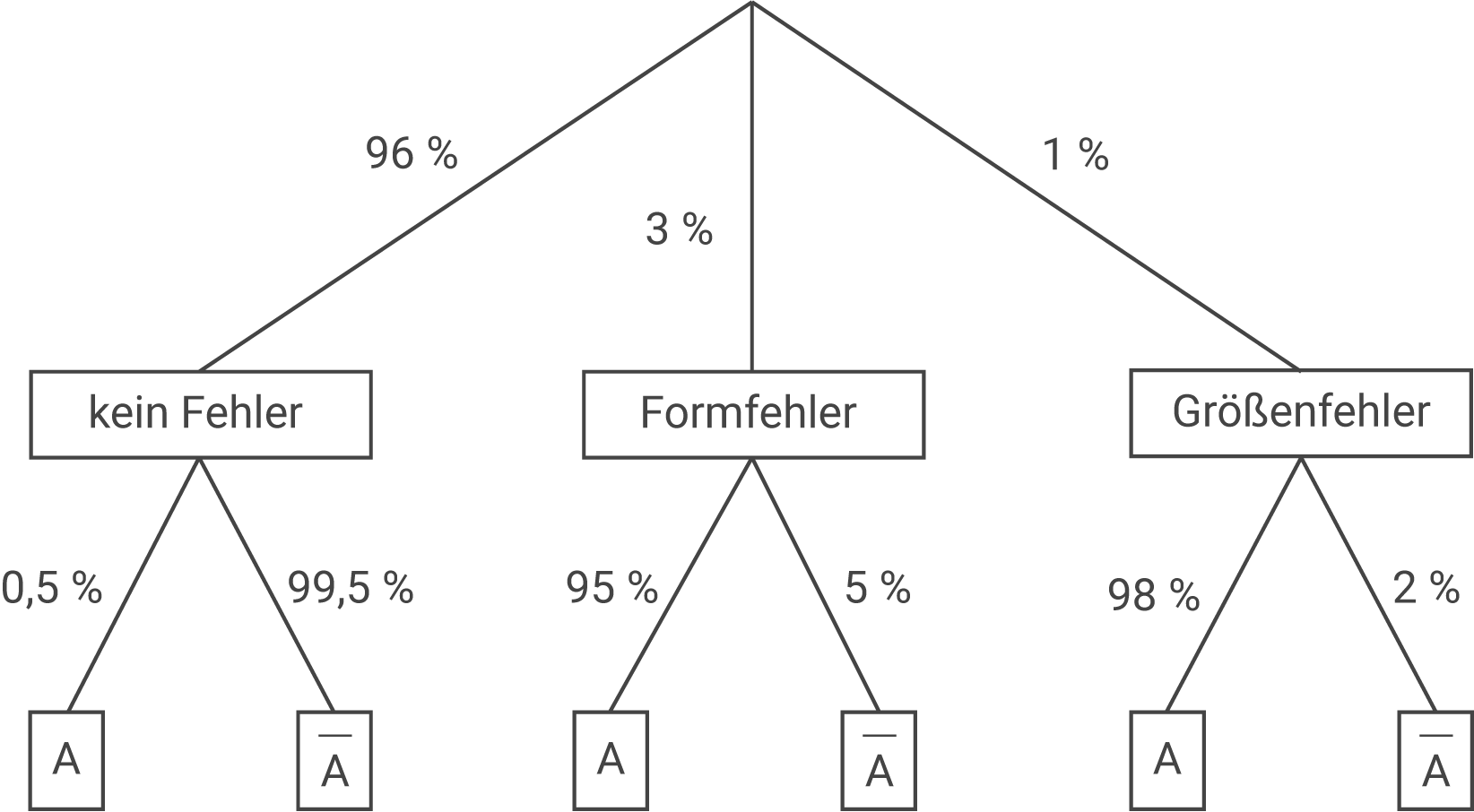
d)
e)
Die Wahrscheinlichkeit ist gegeben durch die Summe der Wahrscheinlichkeiten, dass eine Kugel aussortiert wird, die keinen Fehler oder einen Größenfehler hat, geteilt durch die gesamte Wahrscheinlichkeit dafür, dass eine Kugel aussortiert wird:
Die gesuchte Wahrscheinlichkeit beträgt ungefähr 
f)
Die einzelnen Wahrscheinlichkeiten für die jeweiligen Fehler, dass eine Kugel bei der zweiten Prüfung aussortiert wird, lassen sich wie folgt berechnen:
Die gesuchte Wahrscheinlichkeit ist schließlich gegeben durch 
- ohne Fehler:
- mit Formfehler:
- mit Größenfehler:
g)
Die Zufallsgröße 
beschreibt die Anzahl 
der zurückgegebenen Packungen.
ist 
verteilt.
Zunächst müssen die Werte für besimmt werden, für die gilt:
Da die Anzahl durch eine natürliche Zahl beschrieben wird, ist die Ungleichung für 
erfüllt.
Somit ist die gesuchte Wahrscheinlichkeit gegeben durch 