Pflichtteil

Aufgabe P1

Für jeden Wert von $a(a\in\mathbb{R})$ ist eine Funktion $f_a$ gegeben durch $f_{a}(x)=-x^{2}+a$ $(x\in\mathbb{R})$ .

Begründen Sie mithilfe der Lage des Graphen von $f_1$ im Koordinatensystem, dass

$\mathop{\displaystyle\int}\limits_{-1}^{1}f_{1}(x)\mathrm{dx}>0$ gilt.

(2P)

Bestimmen Sie denjenigen Wert von $a$ , für den $\mathop{\displaystyle\int}\limits_{-1}^{1}f_{a}(x)\mathrm{dx}=0$ gilt.

(3P)

Aufgabe P2

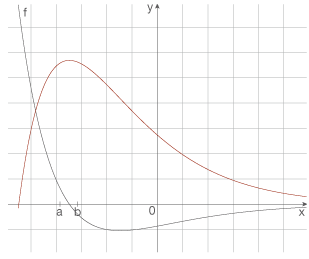
Die Abbildung zeigt den Graphen einer Funktion $f$ .

Beschreiben Sie für $a\leq x\leq b$ den Verlauf des Graphen einer Stammfunktion von $f$ .

(2P)

Skizzieren Sie in der Abbildung den Graphen einer Stammfunktion von $f$ im gesamten dargestellten Bereich.

Graf einer Funktion mit Achsenbeschriftung und Gitterlinien.

(3P)

Aufgabe P3

Gegeben ist die Funktion $f$ mit $f(x)=\mathrm{e}^{x}\cdot\left(2\cdot x+x^{2}\right)$ $(x\in\mathbb{R})$ .

Bestimmen Sie die Nullstellen der Funktion $f$ .

(2P)

Zeigen Sie, dass die Funktion $F$ mit $F(x)=x^{2}\cdot\mathrm{e}^{x}$ $(x\in\mathbb{R})$ eine Stammfunktion von $f$ ist.

(2P)

Zeigen Sie, dass $\mathop{\displaystyle\int}\limits_{-2}^{0}f(x)\mathrm{dx}=-\dfrac{4}{\mathrm{e}^2}$ gilt.

(2P)

Aufgabe P4

In Urne A befinden sich zwei rote und drei weiße Kugeln. Urne B enthält drei rote und zwei weiße Kugeln.
Betrachtet wird folgendes Zufallsexperiment:
Aus Urne A wird eine Kugel zufällig entnommen und in Urne B gelegt; danach wird aus Urne B eine Kugel zufällig entnommen und in Urne A gelegt.

Geben Sie alle Möglichkeiten für den Inhalt der Urne A nach der Durchführung des Zufallsexperiments an.

(2P)

Betrachtet wird das Ereignis E: Nach Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A.
Untersuchen Sie, ob das Ereignis E eine größere Wahrscheinlichkeit als sein Gegenereignis hat.

(3P)

Aufgabe P5

Gegeben sind die Matrix $A$ mit $A=\begin{pmatrix}1&1&0\\1&1&0\\0&0&2\end{pmatrix}$ und der Vektor $\vec{u}$ mit $\vec{u}=\begin{pmatrix}2\\-2\\2\end{pmatrix}$ .

Berechnen Sie das Produkt $A\cdot\vec{u}$ .\newline Geben Sie zwei von $\vec{u}$ verschiedene Vektoren $\vec{v}$ und $\overrightarrow{w}$ an, sodass gilt:

$A\cdot\vec{u}=A\cdot\vec{v}=A\cdot\overrightarrow{w}$ .

(3P)

Zeigen Sie, dass für alle Vektoren $\vec{x}=\begin{pmatrix}0\\4\\2\end{pmatrix}+k\cdot\begin{pmatrix}1\\-1\\0\end{pmatrix}$ $(k\in\mathbb{R})$ gilt: $A\cdot\vec{x}=\begin{pmatrix}4\\4\\4\end{pmatrix}$ .

(2P)

(20P)

Aufgabe P1

a) $\blacktriangleright$ Begründung für positives Integral

Begründe mithilfe der Lage des Graphen von $f_1$ im Koordinatensystem, dass gilt:

$\mathop{\displaystyle\int}\limits_{-1}^{1}\left(-x^{2}+1\right)\mathrm{dx}>0$ .

Schaue dir dafür die Gleichung von $f_1$ an. Dabei stellst du fest, dass der Graph von $f$ eine nach unten geöffnete Normalparabel, die um 1 Einheit nach oben verschoben ist, darstellt. Die Nullstellen sind gegeben durch $\boldsymbol{x_1 = -1}$ und $\boldsymbol{x_2 = 1}$ , das bedeutet, dass der Graph von $f$ im Bereich $-1 \lt x \lt 1$ oberhalb der $x$ -Achse verläuft. Das Integral $\int_{-1}^{1}\left(-x^{2}+1\right)\mathrm{dx}$ ist somit positiv.

b) $\blacktriangleright$ Wert für $\boldsymbol{a}$ bestimmen

Bestimme den Wert von $a$ , für den $\int_{-1}^{1}\left(-x^{2}+a\right)\mathrm{dx}=0$ gilt. Finde dafür zuerst eine Stammfunktion $F$ von $f(x) = -x^2 + a$ . Diese erhältst du mithilfe folgender Formel:

$f(x) = b\cdot x^n \rightarrow F(x) = b\cdot \frac{1}{n+1}\cdot x^{n+1}$

Die Stammfunktion von $f$ ist also gegeben durch $F(x) = -\frac{1}{3} \cdot x^3 + a\cdot x$ . Berechne nun das Integral:

$\begin{array}{rll} \int_{-1}^{1}\left(-x^{2}+a\right)\mathrm{dx}&=&\big[ - \frac{1}{3} x^3 + a\cdot x\big]_{-1}^{1}&\\ &=& -\frac{1}{3} + a - (\frac{1}{3} - a)&\\ &=& -\frac{2}{3} + 2\cdot a&\\ \end{array}$

Setze diesen Term nun gleich Null und löse nach $a$ auf:

$\begin{array}{rll} 0&=& -\frac{2}{3} + 2\cdot a &\scriptsize \mid\;+ \frac{2}{3} \\ \frac{2}{3}&=&2\cdot a&\scriptsize \mid\;: 2 \\ a &=& \frac{1}{3} \end{array}$

Der gesuchte Wert ist gegeben durch $\boldsymbol{a=\frac{1}{3}}$ .

Aufgabe P2

a) $\blacktriangleright$ Graph der Stammfunktion beschreiben

Im Bereich $a\leq x\leq b$ hat der Graph eine Nullstelle mit Vorzeichenwechsel. Das bedeutet, dass der Graph einer Stammfunktion von $f$ in diesem Bereich einen Extrempunkt hat, weil dadurch sowohl die notwendige Bedingung, wie auch die hinreichende Bedingungfür ein Extremum erfüllt sind. Da der Vorzeichenwechsel von $+$ nach $-$ verläuft, ist die Steigung vor der Extremstelle positiv und nach der Extremstelle negativ. Es handelt sich somit um einen Hochpunkt.

b) $\blacktriangleright$ Graphen einer Stammfunktion skizzieren

Du sollst den Graphen einer Stammfunktion von $f$ im gesamten dargestellten Bereich skizzieren. Dieser hat bei $x\approx 3,5$ einen Hochpunkt und für größere $x$ -Werte nähert sich die Funktion $f$ der $x$ -Achse, bleibt jedoch negativ. Das bedeutet, dass der Graph der Stammfunktion nach dem Hochpunkt eine negative Steigung hat. Vor dem Hochpunkt verläuft der Graph der Funktion $f$ oberhalb der $x$ -Achse, deshalb hat der Graph der Stammfunkion vor dem Hochpunkt eine positive Steigung.

Graph mit zwei Kurven auf einem Koordinatensystem, eine rot und eine schwarz.

Aufgabe P3

a) $\blacktriangleright$ Nullstellen bestimmen

Du sollst die Nullstellen der Funktion $f$ angeben. Dafür setzt du den Funktionsterm von $f$ mit Null gleich ( $f(x)=0$ ):

$\begin{array}{rll} 0&=&f(x)&\\ 0&=&(2x+x^2)\cdot \mathrm{e}^x&\scriptsize \mid\; :\; \mathrm{e}^x\; (\mathrm{e}^x>0)\\ 0&=&2x+x^2&\scriptsize \text{(x ausklammern)}\\ 0&=&(2+x)\cdot x&\\ x_1&=&0&\\ x_2&=&-2&\\ \end{array}$

Die Nullstellen von $f$ sind gegeben durch $\boldsymbol{x_1 = 0}$ und $\boldsymbol{x_2 = -2}$ .

b) $\blacktriangleright$ Zeige, dass $F$ eine Stammfunktion von $f$ ist

Zeige, dass die Funktion $F$ mit $F(x)=x^2\cdot\mathrm{e}^x$ , $x\in\mathbb{R}$ , eine Stammfunktion von $f$ ist. Leite die Funktion dafür mit Hilfe der Produktregel ab:

$\boldsymbol{f(x) = g(x) \cdot h(x)}$

$\(\boldsymbol{f$

Hier gilt $g(x) = x^2$ mit $\(g$ und $h(x) = \mathrm e^x$ mit $\(h$ .

$\(\begin{array}{rll} F(x)&=&x^2\cdot \mathrm e^x&\\ F$

Die Ableitung entspricht der Funktion $f$ , somit ist $F$ eine Stammfunktion von $f$ .

c) $\blacktriangleright$ Integral berechnen

Berechne das Integral:

$\begin{array}{rll} \mathop{\displaystyle\int}\limits_{-2}^{0}f(x)\mathrm{dx}&=&\mathop{\displaystyle\int}\limits_{-2}^{0}(2x+x^2)\cdot \mathrm{e}^x \mathrm{dx}&\\ &=&\left[x^2\cdot \mathrm{e}^x\right]_{-2}^0&\\ &=&0^2\cdot \mathrm{e}^0 - ((-2)^2 \cdot \mathrm{e}^{-2})&\\ &=&-\dfrac{4}{\mathrm{e}^2}& \end{array}$

Somit gilt $\boldsymbol{\mathop{\displaystyle\int}\limits_{-2}^{0}f(x)\mathrm{dx}=-\dfrac{4}{\mathrm{e}^2}}$ .

Aufgabe P4

a) $\blacktriangleright$ Möglichkeiten für den Inhalt der Urne A angeben

Du sollst alle Möglichkeiten für den Inhalt der Urne A nach der Durchführung des Zufallsexperiments angeben.

Wenn aus der Urne A eine rote Kugel entnommen wird und wieder eine rote Kugel aus der Urne B in die Urne A gelegt wird, bleibt es bei:

2 rote Kugeln, 3 weiße Kugeln

Wenn aus der Urne A eine weiße Kugel entnommen wird und wieder eine weiße Kugel aus der Urne B in die Urne A gelegt wird, bleibt es bei:

2 rote Kugeln, 3 weiße Kugeln

Wenn aus der Urne A eine rote Kugel entnommen wird und eine weiße Kugel aus der Urne B in die Urne A gelegt wird, gilt für den Inhalt der Urne A:

1 rote Kugel, 4 weiße Kugeln

Wenn aus der Urne A eine weiße Kugel entnommen wird und eine rote Kugel aus der Urne B in die Urne A gelegt wird, gilt für den Inhalt der Urne A:

3 rote Kugeln, 2 weiße Kugeln Die Möglichkeiten für den Inhalt der Urne A sind gegeben durch:

2 rote Kugeln, 3 weiße Kugeln
1 rote Kugel, 4 weiße Kugeln
3 rote Kugeln, 2 weiße Kugeln

b) $\blacktriangleright$ Wahrscheinlichkeit berechnen

Das Ereignis E ist gegeben durch: Nach Durchführung des Zufallsexperiments befinden sich wieder drei weiße Kugeln in Urne A.

Um entscheiden zu können, ob die Wahrscheinlichkeit größer ist, als die des Gegenereignisses, berechne die Wahrscheinlichkeit des Ereignis E. Für das Ereignis E gibt es zwei Möglichkeiten. Entweder es wird sowohl aus Urne A, als auch aus Urne B eine rote Kugel entnommen oder es wird aus beiden Urnen eine weiße Kugel entnommen. Die entsprechende Wahrscheinlichkeit ergibt sich mit Hilfe der Pfadregeln

$\begin{array}{rll} \mathcal{P}(E)& = &\mathcal{P}(\text{A: weiß entnommen, B: weiß entnommen})+\mathcal{P}(\text{A: rot entnommen, B: rot entnommen})&\\ &=&\frac{3}{5} \cdot \frac{3}{6} + \frac{2}{5} \cdot \frac{4}{6}&\\ &=&\frac{3}{10} + \frac{4}{15}&\\ &=&\frac{17}{30}& \end{array}$

Die Wahrscheinlichkeit des Gegenereignisses ist dann gegeben durch:

$\mathcal{P}(\overline{E}) = 1- \mathcal{P}(E) = 1 - \frac{17}{30} = \frac{13}{30}$ .

Die Wahrscheinlichkeit des Ereignis E ist größer als die Wahrscheinlichkeit des Gegenereignisses.

Aufgabe P5

a) $\blacktriangleright$ Matrix-Vektor-Multiplikation

Berechne das Produkt $A\cdot\vec{u}$ . Du berechnest dieses Produkt durch komponentenweise Multiplikation der Einträge der 1., 2. bzw. 3. Zeile von $A$ mit den Elementen von $\vec{u}$ und durch Summation über diese Produkte:

$A\cdot \overrightarrow{u} = \begin{pmatrix}1&1&0\\ 1&1&0\\ 0&0&2\end{pmatrix}\cdot \begin{pmatrix}2\\-2\\2\end{pmatrix} = \begin{pmatrix}1\cdot2 + 1 \cdot (-2) + 0 \cdot 2\\ 1\cdot2 + 1 \cdot (-2) + 0 \cdot 2\\ 0\cdot2 + 0 \cdot (-2) + 2 \cdot 2 \end{pmatrix} = \begin{pmatrix}2 -2 + 0\\ 2 -2 + 0\\ 0 + 0 + 4 \end{pmatrix} = \begin{pmatrix}0 \\ 0 \\ 4\end{pmatrix}$

$\blacktriangleright$ Vektoren bestimmen

Du sollst nun zwei von $\vec{u}$ verschiedene Vektoren $\vec{v}$ und $\overrightarrow{w}$ angeben, sodass gilt:

$A\cdot\vec{u}=A\cdot\vec{v}=A\cdot\overrightarrow{w}$ .

Für die beiden Vektoren muss also gelten, dass bei Multiplikation mit $A$ die ersten beiden Einträge 0 ergeben und der dritte Eintrag $4$ . Somit muss der dritte Eintrag beider Vektoren $2$ sein. Für die ersten beiden Einträge der Vektoren muss gelten, dass diese den gleichen Betrag haben und unterschiedliches Vorzeichen. Das ist der Fall, da diese jeweils mit 1 multipliziert werden und addiert jedoch 0 ergeben müssen.

Somit sind zwei mögliche Vektoren gegeben durch $\boldsymbol{\overrightarrow{v} = \begin{pmatrix}1\\-1\\2\end{pmatrix}}$ und $\boldsymbol{\overrightarrow{w} = \begin{pmatrix}-3\\3\\2\end{pmatrix}}$ .

b) $\blacktriangleright$ Beweise die Aussage

Du sollst zeigen, dass für alle Vektoren $\vec{x}=\begin{pmatrix}0\\4\\2\end{pmatrix}+k\cdot\begin{pmatrix}1\\-1\\0\end{pmatrix}$ $(k\in\mathbb{R})$ gilt: $A\cdot\vec{x}=\begin{pmatrix}4\\4\\4\end{pmatrix}$ . Multipliziere dafür die Matrix $A$ mit $\vec{x}$ :

$\begin{array}{rll} A\cdot \vec{x}&=&\begin{pmatrix}1&1&0\\ 1&1&0\\ 0&0&2\end{pmatrix} \cdot \left(\begin{pmatrix}0\\4\\2\end{pmatrix}+k\cdot\begin{pmatrix}1\\-1\\0\end{pmatrix}\right) & \\ &=&\begin{pmatrix}1&1&0\\ 1&1&0\\ 0&0&2\end{pmatrix} \cdot \begin{pmatrix}0\\4\\2\end{pmatrix} + k\cdot \begin{pmatrix}1&1&0\\ 1&1&0\\ 0&0&2\end{pmatrix} \cdot\begin{pmatrix}1\\-1\\0\end{pmatrix}&\\ &=&\begin{pmatrix}1\cdot 0+1 \cdot 4+0 \cdot 2\\ 1 \cdot 0+1 \cdot 4+0 \cdot 2\\ 0\cdot 0+0\cdot 4+2\cdot 2\end{pmatrix} + k \cdot \begin{pmatrix}1\cdot 1+1 \cdot (-1)+0 \cdot 0\\ 1 \cdot 1+1 \cdot (-1)+0 \cdot 0\\ 0\cdot 1+0\cdot (-1)+2\cdot 0\end{pmatrix}&\\ &=&\begin{pmatrix}0+ 4+0 \\ 0+ 4+0 \\ 0+0+4\end{pmatrix} + k \cdot \begin{pmatrix}1-1+0 \\ 1 -1+0 \\ 0+0+0\end{pmatrix}&\\ &=&\begin{pmatrix}4 \\ 4\\ 4\end{pmatrix} + k \cdot \begin{pmatrix}0 \\ 0 \\ 0\end{pmatrix}&\\ &=&\begin{pmatrix}4 \\ 4\\ 4\end{pmatrix}& \end{array}$

Da das Ergebnis von $\boldsymbol{A\cdot \vec{x}}$ $\boldsymbol{\begin{pmatrix}4\\4\\4\end{pmatrix}}$ und damit unabhängig von $k$ ist , ist somit die Aussage bewiesen.