Pflichtteil

Aufgabe P1

Gegeben ist eine in $\mathbb{R}$ definierte Funktion $f$ mit
$f(x)=x^4-k\cdot x^2,$ wobei $k$ eine positive reelle Zahl ist.
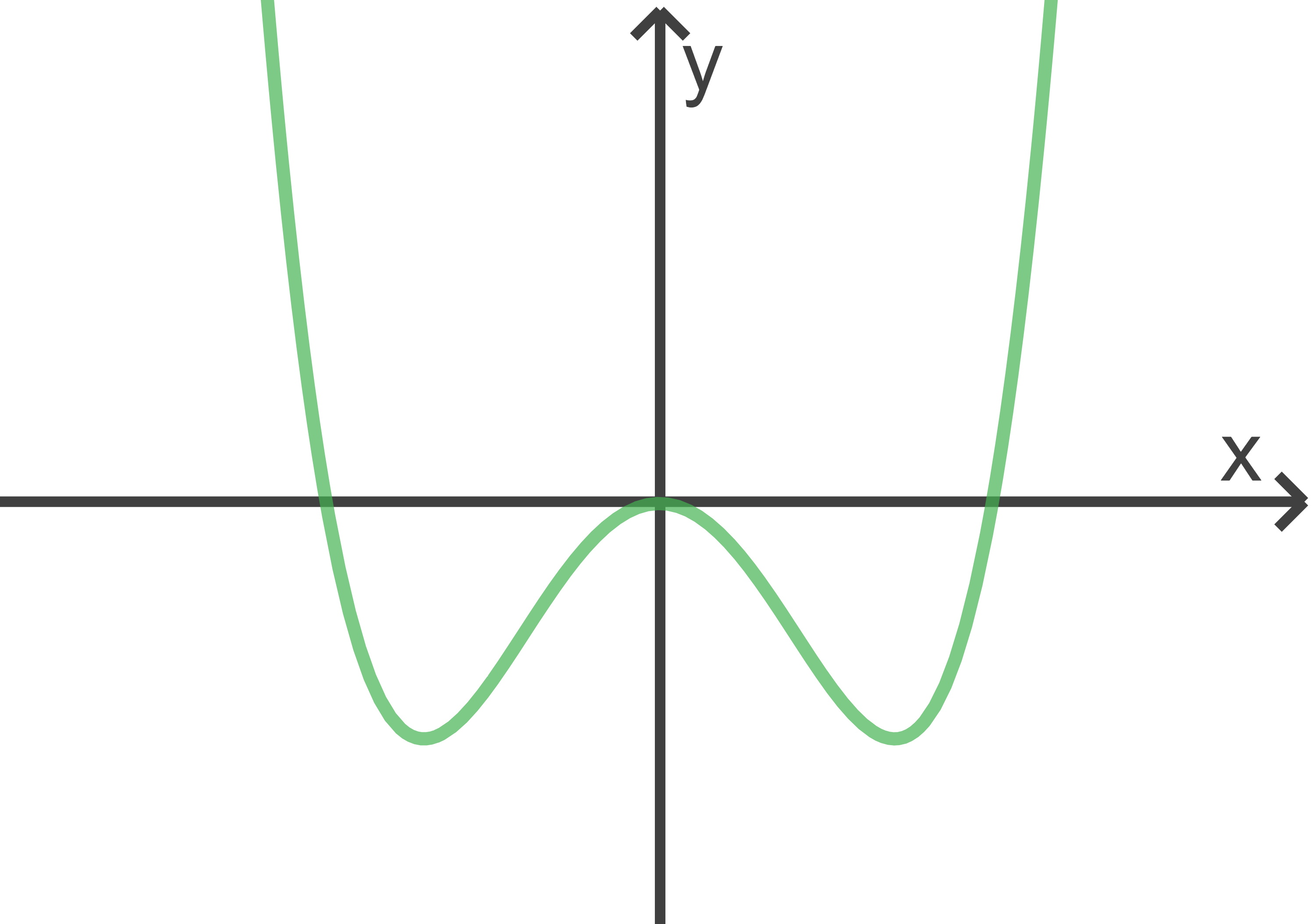
Die Abbildung zeigt den Graphen von $f.$

Graf einer Parabel im Koordinatensystem mit x- und y-Achse.

Zeige, dass $\(f$ eine Gleichung der ersten Ableitungsfunktion ist.

(1 BE)

Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die $y-$ Koordinate $-1.$
Ermittle den Wert von $k.$

(4 BE)

Aufgabe P2

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\sin(x).$ Die Abbildung zeigt den Graphen von $f$ sowie die Tangenten an den Graphen in den dargestellten Schnittpunkten mit der $x-$ Achse.

Graph einer Funktion mit x- und y-Achse, die eine sinusförmige Kurve zeigt.

Zeige, dass diejenige der beiden Tangenten, die durch den Koordinatenursprung verläuft, die Steigung 1 hat.

(1 BE)

Berechne den Inhalt des Flächenstücks, das vom Graphen von $f$ und den beiden Tangenten eingeschlossen wird.

(4 BE)

Aufgabe P3

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f$ und $g.$
Der Graph von $f$ ist symmetrisch bezüglich der $y-$ Achse, der Graph von $g$ ist symmetrisch bezüglich des Koordinatenursprungs. Beide Graphen haben einen Hochpunkt im Punkt $(2\mid 1).$

Gib für die Graphen von $f$ und $g$ jeweils die Koordinaten und die Art eines weiteren Extrempunktes an.

(2 BE)

Untersuche die in $\mathbb{R}$ definierte Funktion $h$ mit $h(x)=f(x)\cdot \left(g(x)\right)^3$ im Hinblick auf eine mögliche Symmetrie ihres Graphen.

(3 BE)

Aufgabe P4

Gegeben sind der Punkt $P(-1\mid 7\mid 2)$ und die Ebene $E:x_1+3x_2=0.$

Zeige, dass der Punkt $P$ nicht in $E$ liegt.

(1 BE)

Bestimme die Koordinaten des Punktes, der entsteht, wenn $P$ an $E$ gespiegelt wird.

(4 BE)

Aufgabe P5

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n=100$ und $p.$
Der Erwartungswert von $X$ ist 50.

Berechne die Standardabweichung von $X.$

(3 BE)

Die Wahrscheinlichkeit $P(X\geq 61)$ beträgt etwa 2 %.
Bestimme damit einen Näherungswert für die Wahrscheinlichkeit $P(40\leq X\leq 60).$

(2 BE)

Aufgabe P6

In einem Behälter befinden sich Kugeln, von denen jede dritte gelb ist.

Aus dem Behälter wird zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt.
Berechne die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind.

(1 BE)

Im Behälter werden zwei gelbe Kugeln durch zwei blaue Kugeln ersetzt. Anschließend wird aus dem Behälter erneut zweimal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. Die Wahrscheinlichkeit dafür, dass beide Kugeln gelb sind, beträgt nun $\dfrac{1}{16}.$
Ermittle, wie viele gelbe Kugeln sich nach dem beschriebenen Vorgang im Behälter befinden.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung P1

Durch Ableiten und Ausklammern ergibt sich:

$\(\begin{array}[t]{rll} f$

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Nach dem Satz vom Nullprodukt muss entweder $2x=0$ oder $2x^2-k=0$ sein. Damit liegt die erste Extremstelle bei $x_1=0$ . Weiter ist:

$\begin{array}[t]{rll} 2x^2-k &=&0 &\quad \scriptsize \mid\; +k \\[5pt] 2x^2 &=&k &\quad \scriptsize \mid\;:2 \\[5pt] x^2 &=&\dfrac{k}{2} &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt] x_{2/3} &=&\pm \sqrt{\dfrac{k}{2}}. &\quad \scriptsize \\[5pt] \end{array}$

Damit hat $f$ zwei weitere Extremstellen bei $x_2= \sqrt{\dfrac{k}{2}}$ und $x_3=- \sqrt{\dfrac{k}{2}}$ .

Auf die hinreichende Bedingung kann verzichtet werden, da die Existenz zweier Tiefpunkte durch die Aufgabenstellung gegeben ist. Zwei Tiefpunkte können nicht aufeinander folgen, daher liegt bei $x_1=0$ ein Hochpunkt und bei $x_2$ und $x_3$ jeweils ein Tiefpunkt.

2. Schritt: Berechnung des Wertes k

Für $k\gt0$ und $x_2$ gilt:

$f\left(\sqrt{\dfrac{k}{2}}\right)$ $= \left(\sqrt{\dfrac{k}{2}}\right)^4-k \cdot \left(\sqrt{\dfrac{k}{2}}\right)^2$ $=\dfrac{k^2}{4}-k \cdot \dfrac{k}{2}$ $=\dfrac{k^2}{4}-\dfrac{k^2}{2}=-\dfrac{k^2}{4}$

Für $k>0$ und $x_3$ gilt ebenfalls:

$f\left(-\sqrt{\dfrac{k}{2}}\right) = -\dfrac{k^2}{4}$

Da die Tiefpunkte die $y$ -Koordinate $-1$ haben, lässt sich $k$ durch folgende Gleichung ermitteln:

$\begin{array}[t]{rll} -\dfrac{k^2}{4}&=&-1 &\quad \scriptsize \mid\; \cdot(-4)\\[5pt] k^2&=&4 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt] k&=&2 \end{array}$

Für $k=2$ haben die beiden Tiefpunkte des Graphen von $f$ die $y$ -Koordinate $-1.$

Lösung P2

Die Tangente durch den Koordinatenursprung hat die gleiche Steigung wie die Funktion $f$ in diesem Punkt.

1. Schritt: Ableitung aufstellen

$\(f$

2. Schritt: Steigung berechnen im Ursprung

$\(f$

Es müssen die Intervalle von $x=0$ bis $x=\frac{\pi}{2}$ und von $x=\frac{\pi}{2}$ bis $x=\pi$ unterteilt werden. Da der Sinus symmetrisch ist, sind die Flächeninhalte dieser beiden Flächen gleich groß. Deswegen reicht es den Flächeninhalt einer Fläche zu berechnen und diesen zu verdoppeln.

1. Schritt: Tangentengleichung aufstellen

Nach a) hat die Tagente durch den Punkt $(0 \mid 0)$ die Steigung 1. Damit ist die Tangentengleichung $t(x)=x.$

2. Schritt: Flächeninhalt berechnen

Vollständigen Rechenweg anzeigen

$2\cdot\displaystyle\int_{0}^{\dfrac{\pi}{2}}(t(x)-f(x))\;\mathrm dx =\dfrac{\pi^2}{4}-2$

Der Inhalt des gesuchten Flächenstücks ist gegeben durch $\dfrac{\pi^2}{4}-2\, \;\text{FE}.$

Lösung P3

Da der Graph von $f$ symmetrisch bezüglich der $y$ -Achse ist, existiert ein weiterer Hochpunkt des Graphen in $(-2 \mid 1).$
Aufgrund der Punktsymmetrie bezüglich des Koordinatenursprungs hat der Graph von $g$ einen Tiefpunkt in $(-2 \mid -1).$

Wegen der Symmetrien der Graphen von $f$ und $g$ gilt :

$\begin{array}[t]{rll} f(-x) &=&f(x) &\quad \scriptsize \\[5pt] g(-x) &=&-g(x) &\quad \scriptsize \\[5pt] \end{array}$

Damit folgt für die Symmetrie des Graphen von $h$ :

Vollständigen Rechenweg anzeigen

$h(-x)=-h(x)$

Der Graph von $h$ ist symmetrisch zum Koordinatenursprung.

Lösung P4

Einsetzen des Punktes $P$ in die Ebenengleichung liefert:

$\begin{array}[t]{rll} x_1+3x_2 &=&0 &\quad \scriptsize \\[5pt] -1+3\cdot 7 &\not =&0&\quad \scriptsize \\[5pt] 20 &\not =&0&\quad \scriptsize \\[5pt] \end{array}$

Damit liegt der Punkt $P$ nicht in der Ebene $E.$

1. Schritt: Normalenvektor ablesen

Ein Normalenvektor der Ebene $E$ ist gegeben durch $\overrightarrow{n}=\pmatrix{1\\3\\0}.$

2. Schritt: Gleichung der Gerade die senkrecht zu $E$ durch $P$ verläuft, aufstellen

$g: \overrightarrow{x} = \pmatrix{-1\\7\\2}+t \cdot \pmatrix{1\\3\\0}$

3. Schritt: Schnittpunkt von $g$ und $E$ berechnen

Für den Schnittpunkt muss $g$ und $E$ einsetzt werden.

Vollständigen Rechenweg anzeigen

$t=-2$

Dieses $t$ müsste für den Schnittpunkt in $g$ eingesetzt werden. Da jedoch nicht nach dem Schnittpunkt, sondern nach dem Spiegelpunkt gefragt ist, muss das doppelte von $t$ eingesetzt werden. Die Strecke von $P$ zu $E$ und von $E$ zum Spiegelpunkt sind gleich lang.

4. Schritt: Spiegelpunkt $\(P$ berechnen

$\(P$ $=\pmatrix{-5\\-5\\2}$

Die Koordinaten des gesuchten Punkts sind $\(P$ .

Lösung P5

Um die Standardabweichung zu berechnen, muss zuerst $p$ ermittelt werden. Es gilt:

$\begin{array}[t]{rll} E(X)&=& 50 &\quad \scriptsize \\[5pt] 100\cdot p&=& 50 &\quad \scriptsize \mid\;:100 \\[5pt] p&=& 0,5 &\quad \scriptsize \\[5pt] \end{array}$

Damit ist die Standardabweichung gegeben durch $\sigma(X)= \sqrt{100 \cdot 0,5^2}=5.$

Für $p=0,5$ ist die Binomialverteilung symmetrisch um den Erwartungswert $E(X)=50.$
Damit gilt $P(X \geq 61)=P(X\leq 39)\approx 2\%.$

Daraus folgt:

Vollständigen Rechenweg anzeigen

$P(40\le X\le 60)=96\%$

Ein Näherungswert für die gesuchte Wahrscheinlichkeit ist $96\%.$

Lösung P6

Die Wahrscheinlichkeit, eine gelbe Kugel zu ziehen, beträgt $p=\dfrac{1}{3}.$ Die Wahrscheinlichkeit dafür, dass zwei hintereinander gezogene Kugeln gelb sind, ist dann gegeben durch $\dfrac{1}{3} \cdot \dfrac{1}{3} = \dfrac{1}{9}.$

Für die Wahrscheinlichkeit $\(p$ eine gelbe Kugel zu ziehen, gilt $\(p$ und damit $\(p$ Daraus lässt sich folgern, dass jede vierte Kugel gelb ist.

$x$ ist die gesuchte Anzahl an gelben Kugeln nach dem Tausch. Dann liegen insgesamt $4\cdot x$ Kugeln im Behälter.
Vor dem Tausch mit den blauen Kugeln, gab es zwei gelbe Kugeln mehr, also ingesamt $x+2$ . Die Wahscheinlichkeit vor dem Tausch eine gelbe Kugel zu ziehen, ist damit $p=\frac{x+2}{4x}$ . Aus der Aufgabenstellung ist außerdem bekannt, dass vor dem Tausch jede dritte Kugel gelb war, also dass $p=\frac{1}{3}$ ist. Durch Gleichsetzten der Wahrscheinlichkeit $p$ ergibt sich $x$ .

$\begin{array}[t]{rll} \dfrac{x+2}{4\cdot x}&=&\dfrac{1}{3} &\quad \scriptsize \mid\; \cdot (4\cdot x) \; \mid\; \cdot 3\\[5pt] 3x+6&=&4\cdot x &\quad \scriptsize \mid\;-3x \\[5pt] 6&=&x \end{array}$

Nach dem beschriebenen Vorgang befinden sich $6$ gelbe Kugeln im Behälter.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?