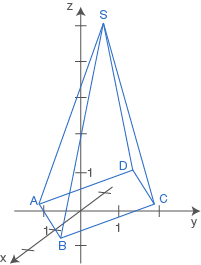
a)
 Zeigen, dass das Dreieck
Zeigen, dass das Dreieck  gleischenklig ist
gleischenklig ist
Ein Dreieck ist gleichschenklig, wenn zwei der drei Seiten gleich lang sind. Bilde als erstes die Verbindungsvektoren

,

und

. Die Länge eines Vektors ist gerade der
Betrag des Vektors.
Aus

folgt, dass die beiden Vektoren

und

gleich lang sind. Somit hast du gezeigt, dass das Dreieck

gleichschenklig ist.
 Zeige, dass das Dreieck am Punkt
Zeige, dass das Dreieck am Punkt  einen rechten Winkel hat
einen rechten Winkel hat
Das Dreieck besitzt im Punkt

einen rechten Winkel, wenn die beiden Vektoren

und

senkrecht zueinander stehen. Das Skalarprodukt der Vektoren

und

muss somit null sein.
Da das Skalarprodukt null ist, stehen die Vektoren

und

senkrecht aufeinander. Das Dreieck

hat im Punkt

einen rechten Winkel.
 Koordinaten des Punktes
Koordinaten des Punktes  berechnen
berechnen
In dieser Aufgabe sollst du die Koordinaten des Punktes

berechnen, sodass die Punkte

,

,

und

die Eckpunkte eines Quadrates sind.
Um das Dreieck zu einem Quadrat zu ergänzen, kannst du den Vektor

an den Ortsvektor, der zum Punkt

zeigt addieren.
Die Koordinaten des gesuchten Punktes

kannst du jetzt ablesen.
Die Koordinaten des vierten Punktes sind

.
 Winkel zwischen der Streck
Winkel zwischen der Streck  und der Diagonalen
und der Diagonalen  berechnen
berechnen
Den Winkel zwischen zwei Vektoren kannst du mit der
Cosinus-Formel berechnen.
Um den Winkel zwischen den beiden Strecken zu berechnen, bildest du als erstes die beiden Verbindungsvektoren

und

und setzt diese anschließend in die Cosinus-Formel ein.


Der Winkel zwischen den Strecken

und

beträgt

.
b)
 Überprüfen, ob es Punkte auf der Strecke
Überprüfen, ob es Punkte auf der Strecke  gibt, die einen Abstand von
gibt, die einen Abstand von  zum Punkt
zum Punkt  haben
haben
Um zu untersuchen, ob es Punkte auf der Strecke

gibt, die zum Punkt

einen Abstand von 4,5 haben, bildest du als erstes eine Gerade durch die Punkte

und

, bestimmst den allgemeinen Punkt dieser Geraden und berechnest anschließend den Abstand zwischen der Gerade und dem Punkt, indem du den Betrag des Verbindungsvektors

berechnest. Wichtig ist, dass der Parameter größer als null und kleiner als eins sein muss, denn sonst liegt der Punkt nicht mehr auf der Strecke

.
1. Schritt: Gerade g bestimmen
Wähle einen Ortsvektor der zu einem Punkt zeigt als Stützvektor der Geraden und den Verbindungsvektor der zwei Punkte als Richtungsvektor.
2. Schritt: allgemeinen Punkt der Geraden ablesen
Der allgemeine Punkt der Geraden

hat die Koordinaten

.
3. Schritt: Abstand berechnen
Bilde als erstes den Verbindungsvektor zwischen dem allgemeinen Punkt

und dem Punkt

.

Der Betrag dieses Vektors soll nun gerade 4,5 sein. Du erhältst eine Gleichung. Löse diese nach

auf.
Verwende die abc-Formel um mögliche Werte für

zu erhalten.
Da

gibt es genau einen Punkt auf der Strecke

der zum Punkt

einen Abstand von

![\([LE]\)](https://mathjax.schullv.de/021ce998fc1fc3c3fc445e9fbd10644a6c328897fb5f2808fc102e186dbdd451?color=5a5a5a)
hat.
 Flächeninhalt des Quadrats berechnen
Flächeninhalt des Quadrats berechnen
In dieser Aufgabe sollst du den Flächeninhalt eines Quadrates berechnen, dessen Eckpunkt auf der Seitenkante der Pyramide liegen. Dieser Punkt teilt die Strecke vom Punkt

zum Eckpunkt im Verhältnis

. Mit Hilfe des zweiten Strahlensatzes kannst du die Länge der Strecke des Quadrats

berechnen.
Es gilt:

Diese Gleichung kannst du nach

umstellen.

Den Flächeinhalt des Quadrats berechnest du, indem du die Länge der Seitenkante quadrierst.
Im Aufgabenteil a) hast du die Länge der Seitenkante

schon berechnet. Setzt die Länge in die Gleichung ein.

Das Quadrat hat einen Flächeninhalt von
![\(A_{Quadrat}= \dfrac{8a^2}{(a+b)^2}\; [FE] \)](https://mathjax.schullv.de/b4b725d520c2614c9b1c8149833b1dcf6ee13dcebf75f2c4131e45568659c93d?color=5a5a5a)
.
c)
 Prüfen, ob es einen Punkt in der Ebene
Prüfen, ob es einen Punkt in der Ebene  gibt, der drei gleiche Koordinaten hat
gibt, der drei gleiche Koordinaten hat
Um dies zu prüfen, stellst du als erstes die Ebenengleichung in Parameterform der Ebene

auf und berechnest mit dieser die Koordinatengleichung der Ebene

.
Setze dann einen Punkt mit drei gleichen Koordinaten, zum Beispiel

, in die Koordinatengleichung ein. Ist die Gleichung lösbar, liegt ein Punkt mit drei gleichen Koordinaten in der Ebene

.
1. Schritt: Ebenengleichung in Paramterform aufstellen
Bestimme mit den Punkten

,

und

eine Ebenengleichung.
2. Schritt: Ebenegleichung in Koordinatenform
Mit Hilfe des Vektorprodukts der beiden Spannvektoren kannst du einen
Normalenvektor der Ebene

berechnen.

Diesen Vektor kannst du noch mit

kürzen.

Die Normalengleichung der Ebene

ist dann:

Setze die Koordinaten des Punktes

ein, um

zu berechnen.

Eine Ebenengleichung in Koordinatenform ist:
 3. Schritt: Punkt mit drei gleichen Koordinaten einsetzen
3. Schritt: Punkt mit drei gleichen Koordinaten einsetzen
Setze den Punkt mit den Koordinaten

in die Ebenengleichung ein und löse die Gleichung nach

auf.
![\(\begin{array}[t]{rll}
5x + 5x +2x&=& 32 \\[5pt]
12x&=& 32 &\quad \scriptsize \mid\; :12 \\[5pt]
x&=& \frac{8}{3}
\end{array}\)](https://mathjax.schullv.de/61ea793d9f4199f6ddeea5a0e2d44909f29ec090a5ca0571889011a57ad5cfe1?color=5a5a5a)
In der Ebene

gibt es einen Punkt bei dem alle Koordinaten gleich sind. Dieser Punkt hat die Koordinaten

.
 Prüfen, ob jede beliebige Ebene einen Punkt hat, der drei gleiche Koordinaten hat
Prüfen, ob jede beliebige Ebene einen Punkt hat, der drei gleiche Koordinaten hat
Hier kannst du ähnlich wie im Aufgabenteil zuvor vorgehen. Bestimme eine allgemeine Form einer Ebene in Koordinatenform und setze einen beliebigen Punkt mit drei gleichen Koordinaten in die Ebenengleichung ein.

Setze den Punkt

in die Ebenengleichung ein und löse die Gleichung nach

auf.
In einer beliebigen Ebene gibt es einen Punkt, bei dem alle drei Koordinaten gleich sind, wenn gilt

. Somit liegt nicht in jeder Ebene ein Punkt, bei dem alle drei Koordinaten gleich sind.
 ist gleichschenklig und rechtwinklig mit dem rechten Winkel im Punkt
ist gleichschenklig und rechtwinklig mit dem rechten Winkel im Punkt  .
.
 so, dass
so, dass  ,
,  ,
,  und
und  Eckpunkte eines Quadrats sind.
Berechne den Winkel zwischen der Strecke
Eckpunkte eines Quadrats sind.
Berechne den Winkel zwischen der Strecke  und der Diagonalen
und der Diagonalen  .
.
 gibt, die zu
gibt, die zu  den Abstand
den Abstand  haben.
Auf jeder Seitenkante der Pyramide gibt es einen Punkt, der die Strecke von
haben.
Auf jeder Seitenkante der Pyramide gibt es einen Punkt, der die Strecke von  zum jeweiligen Eckpunkt im Verhältnis
zum jeweiligen Eckpunkt im Verhältnis  teilt. Diese Punkte bilden ein Quadrat.
teilt. Diese Punkte bilden ein Quadrat.
 ,
,  und
und  liegen in einer Ebene
liegen in einer Ebene  .
.
 einen Punkt gibt, der drei gleiche Koordinaten hat. Untersuche, ob jede beliebige Ebene einen Punkt hat, der drei gleiche Koordinaten hat.
einen Punkt gibt, der drei gleiche Koordinaten hat. Untersuche, ob jede beliebige Ebene einen Punkt hat, der drei gleiche Koordinaten hat.