Aufgabe 1B

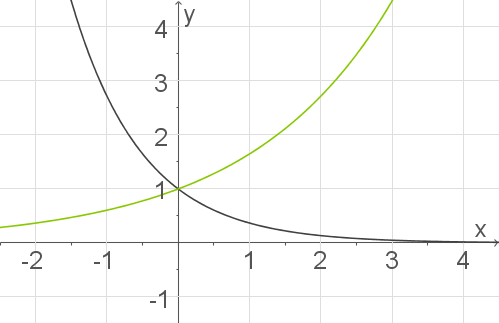
Die Abbildung zeigt die Graphen der Funktionen für und . Entscheide, welche der Funktionen zu welchem Graphen gehört. Berechne die -Koordinate des Punktes, in dem die Tangente an den Graphen von die Steigung hat. Für jeden Wert von bezeichnet die Tangente an den Graphen von im Punkt . Zeige, dass es zu jedem Parameter einen davon verschiedenen Parameter gibt, sodass sich die Tangenten und senkrecht schneiden. Ohne Nachweis kannst du verwenden: Wenn für die Steigungen und zweier Geraden die Beziehung gilt: , dann stehen die zugehörigen Geraden senkrecht aufeinander. Jede Tangente hat eine Nullstelle. Die Nullstelle der Tangente wird mit bezeichnet und die Nullstelle der Tangente wird mit bezeichnet. Begründe, dass der Wert von doppelt so groß ist wie der Wert von , wenn halb so groß ist wie .

Die Funktionen werden nun mit den folgenden Bedingungen betrachtet: und . Für jeden Wert von wird dem Graphen von ein rechtwinkliges Dreieck einbeschrieben. Für eine Stelle sind , und die Eckpunkte. Bei Rotation dieser Dreiecke um die -Achse entstehen Kegel. Zeige, dass für die Volumen der Kegel gilt: . Untersuche, ob die Kegel mit dem maximalen Volumen für jeden Wert des Parameters denselben Grundkreisradius haben. Ohne Nachweis kannst du verwenden: und .

Für werden nun die Funktion sowie die Funktion mit der Gleichung betrachtet. bezeichnet die Tangente an den Graphen von an der Stelle und bezeichnet die Tangenten an den Graphen von an dieser Stelle . Es gibt eine Stelle, an der die Tangenten und parallel zueinander verlaufen. Bestimme die Differenz der y-Achsenabschnitte dieser parallelen Tangenten. Die Graphen von und schneiden sich an einer Stelle und begrenzen zwei Flächen: Eine liegt rechts von und wird rechts von der -Achse begrenzt und eine liegt links von und wird von der Geraden zu begrenzt. Bestimme das Verhältnis der Inhalte beider Flächen. Die Funktion wird nun für alle betrachtet. Untersuche, welche Steigungswerte der Graph von genau einmal und welche Steigungswerte er genau zweimal annimmt.

Begründe ausgehend von den Integralen und , dass für gilt: .

  Funktionsgraphen zuordnen Um festzustellen, welcher Graph die Funktionsschar für den Parameter und zeigt, betrachtest du zuerst die Unterschiede der beiden Graphen. Eine „normale“ -Funktion verläuft monoton wachsend auf ganz und besitzt den Ordinatenabschnitt . Betrachtest du den Term der Funktion , lässt sich dieser schreiben als . Dies ist eine gebrochenrationale Funktion. Der Nenner, die -Funktion, wächst dabei, wie du bereits weißt, monoton an. Der Funktionswert wird somit für steigende Argumente kleiner. Der grüne Graph zeigt eine -Funktion mit positivem Exponenten, in diesem Fall mit . Der andere Graph fällt für steigende -Werte und zeigt den Graph von .   -Koordinate berechnen Du sollst die Stelle bzw. -Koordinate berechnen, bei welchem die Tangente an den Graphen von die Steigung besitzt. Die Tangentensteigung ist allerdings immer gleich der Steigung der Funktion im Berührpunkt ihres Graphen. Du berechnest somit die Stelle, an welcher gilt. 1. Schritt: Funktion aufstellen und Ableitung berechnen Um diese Gleichung zu lösen, benötigst du die Ableitung . Die Funktion lautet dabei: Die Ableitung bestimmst du mit der Kettenregel: Dabei gilt und . Du erhälst die Funktionsgleichung der Ableitung: 2. Schritt: Gleichung lösen Mit dieser Funktionsgleichung löst du die Gleichung , um die -Koordinate zu bestimmen: Die Tangente an den Graphen von hat an der Stelle die Steigung .   Orthogonalität nachweisen Gegeben sind die Tangenten , welche den Graphen im Punkt berühren. Du sollst nachweisen, dass es einen Parameter gibt, sodass die zugehörige Tangente , welche den Graphen im Punkt berührt, die Tangente senkrecht schneidet. Aus der Aufgabenstellung weißt du, dass für zwei sich senkrecht schneidende Geraden und Tangenten mit den Steigungen und gilt: 1. Schritt: Steigung berechnen Für die Steigungen der Tangenten benötigst du den Term der Ableitung, welchen du erneut mit der Kettenregel erhälst: Im Punkt , beziehungsweise an der Stelle hat der Graph von die Steigung: Die Tangente besitzt im Punkt somit die Steigung . 2. Schritt: Parameter bestimmen Um den Parameter zu bestimmen, sodass und sich senkrecht schneiden, wendest du die Bedingung aus der Aufgabenstellung an, und löst die Gleichung nach auf: Da gilt, kannst du für alle das zugehörige berechnen. Somit gibt es immer Tangenten, welche sich an der Stelle senkrecht schneiden.   Verhältnis der Tangenten und Nullstellen Parameter begründen Du sollst begründen, warum doppelt so groß ist wie , wenn die Nullstelle der Tangente halb so weit vom Ursprung entfernt ist wie . Zur Vereinfachung dieses Problems bestimmst du zuerst die Funktionsgleichung der Tangente und die zugehörige Nullstelle . 1. Schritt: Funktionsgleichung bestimmen Alle Tangenten verlaufen durch den Punkt und besitzen die Steigung . Lösungsweg A: Allgemeine Tangentengleichung Alle Tangenten an eine Funktion lassen sich in folgender Form schreiben. Dabei bezeichnet die Stelle an welcher die Tangente an der Graphen angelegt wird. Du benötigst die Tangentengleichug an der Stelle , dort gilt und . Die Tangenten durch an die Graphen von haben die Form . Lösungsweg B: Allgemeine Geradengleichung Alle Tangenten sind Geraden und lassen sich somit durch die Form ausdrücken. Du benötigst die Steigung sowie den Ordinatenabschnitt um die Tangente an den Graphen durch den Punkt zu bestimmen. Die Tangenten durch an die Graphen von haben die Form . 2. Schritt: Nullstelle berechnen Alle Nullstellen zeichen sich durch den -Wert aus. Du setzt die Geradengleichung und löst sie nach der Nullstelle auf. Die Nullstellen der Tangenten haben den -Wert . 3. Schritt: Aussage begründen Die Tangenten und haben ihre Nullstellen bei beziehungsweise . Der Aufgabenstellung nach, ist zu prüfen wie und im Verhältnis stehen wenn halb so groß ist wie , also gilt. Betrachte die Nullstelle der Tangente : Damit ist gezeigt, dass gilt, wenn gilt.

  Volumen der Kegel bestimmen Lösungsweg A: Rotationsvolumen Um das Volumen des Kegels zu berechnen, bestimmst du die Geradengleichung der Hypothenuse des rechtwinkligen Dreiecks, welche die Punkte und verbindet und berechnest daraus dann das Rotationsvolumen. 1. Schritt: Geradengleichung bestimmen Die Gerade verbindet die Punkte und . Du benötigst Steigung udn Ordinatenabschnitt. Die Steigung bestimmst du mittels eines Steigungsdreiecks: Die Steigung der Geraden ist . Da es sich um eine Ursprungsgerade handelt, gilt für den Ordinatenabschnitt . Du erhälst die Geradengleichung: 2. Schritt: Rotatiosnvolumen bestimmen Das Rotationsvolumen einer Funktion ist zwischen den Stellen und definiert durch: Für die Geradengleichung als Funktion und sowie als Grenzen ergibt sich das Volumen des Kegels mit: Der Kegel hat das Volumen . Lösungsweg B: Kegelvolumen Du kannst den Funktionswert als Radius der Grundfläche eines liegenden Kegels mit der Höhe verwenden. Für das Volumen eines Kegels gilt: Mit dem Radius und der Höhe ergibt sich für das Volumen : Der Kegel hat das Volumen .   Unabhängigkeit des maximalen Volumens nachweisen Um zu überprüfen, ob der Grundkreisradius unabhängig vom Parameter ist, bestimmst du zuerst den Wert für welcher maximiert. Die dafür nötige erste und zweite Ableitung ist in der Aufgabenstellunng gegeben mit: 1. Schritt: Ableitung null setzen Zur Bestimmung der Extremstellen der Volumenfunktion setzt du deren erste Ableitung : An der Stelle hat die Volumenfunktion einen Extrempunkt. 2. Schritt: Art des Extrempunkts prüfen Zur Prüfung der Art des Extrempunktes setzt du diesen in die zweite Ableitung ein. Für ein Maximum und Hochpunkt ist die zweite Ableitung negativ. Da ist der Term ebenfalls kleiner als . An der Stelle liegt ein Hochpunkt vor. Das Volumen ist an dieser Stelle somit maximal. 3. Schritt: Grundkreisradius berechnen Mit der Stelle berechnest du den Grundkreisradius : Die Kegel mit dem maximalen Volumen haben den Grundkreisradius , dieser ist unabhängig von und somit für alle Kegel an allen Funktionen der Schar gleich.

Stelle, an der Tangenten parallel zueinander sind bestimmen Du sollst die Stelle bestimmen, an der die Tangenten an und parallel zueinander verlaufen, also die gleiche Steigung besitzen. Da die Steigung einer Tangente an der Stelle der Steigung der Funktion an der Stelle entspricht, musst du und gleichsetzten und nach auflösen. Nach dem Satz vom Nullprodukt ist die Gleichung genau dann erfüllt, wenn einer der beiden Faktoren Null ist. Die Exponentialfunktion ist für kein Null. Damit ist die Gleichung nur erfüllt, wenn gilt. Die beiden Tangenten verlaufen an der Stelle parallel zueinander. Differenz der Achsen Abschnitte bestimmen Die Tangentengleichungen an der Stelle kannst du mit den folgenden Gleichungen bestimmen: Die Achsen Abschnitte sind und . Die Differenz der Achsen Abschnitte ist: Die Differenz der Achsenabschnitte ist . Konzept zu Berechnung des Verhältnises der Flächeninhalte erstellen Um das Verhältnis der Flächeninhalte zu bestimmen musst du die Flächeninhalte zunächst berechnen. Es handelt sich um Flächeninhalte zwischen und im Intervall und . Flächeninhalte zwischen Kurven berechnest du mit dem Integral über den Betrag der Differenz von und . Bevor du die Integrale berechnen kannst, musst du bestimmen. bestimmen Bestimme den Schnittpunkt der Kurven und . Der Schnittpunkt und damit die unbekannte Integrationsgrenze ist Flächeninhalte zwischen den Kurven bestimmen Berechne zuerst die Fläche zwischen und im Intervall und nenne diese Fläche . In diesem Intervall verläuft oberhalb von . Berechne den Wert des Integrals mit deinem Taschenrechner. Berechne als Nächstes die Fläche zwischen und im Intervall und nenne diese Fläche . In diesem Intervall verläuft oberhalb von . Berechne den Wert des Integrals mit deinem Taschenrechner. Das Verhältnis der Flächen ist: . Häufigkeit der Steigungswerte analysieren Du sollst untersuchen, welche Steigungswerte der Graph von genau einmal bzw. genau zweimal annimmt. Untersuche dazu die Funktion . Betrachte als erstes den Wert . Dieser Steigungswert wird von an allen Stellen angenommen, an denen die Ableitungsfunktion Null ist. Da für jedes größer als Null ist, halt die einzige Nullstelle . Der Steigungswert wird also einmal angenommen. Betrachte als Nächstes die Werte . Für diese Werte ist streng monoton fallend. Außerdem ist . Jede negative reelle Zahl wird genau einmal als Steigungswert angenommen. Betrachte als Letztes die Werte . Für diese Werte ist positiv und hat ein Maximum bei . Da für , nimmt alle Steigungswerte zwischen und genau zwiemal und den Maximalwert genau einmal an.

  Ungleichung begründen Du sollst mit Hilfe der beiden Integrale und die Abschätzung für alle nachweisen. Untersuchte dazu die Integranden und . Für haben beide den gleichen Funktionswert . Allerdings ist die Steigung der -Funktion immer größer als die der Gerade, deren Steigung konstant ist. Somit gilt für alle -Werte größer , dass größer als ist. Bestimmst du den Wert derIntegrale, erhältst du: Damit ist die Ungleichung nachgewiesen.