Aufgabe 1A
Gegeben ist die Schar der in  definierten Funktion
definierten Funktion  mit
mit  mit
mit  Die zugehörigen Graphen sind symmetrisch bezüglich des Koordinatenursprungs.
Die zugehörigen Graphen sind symmetrisch bezüglich des Koordinatenursprungs.
Es gilt:
Es gilt:
a)
Zeige, dass  genau eine Nullstelle hat.
genau eine Nullstelle hat.
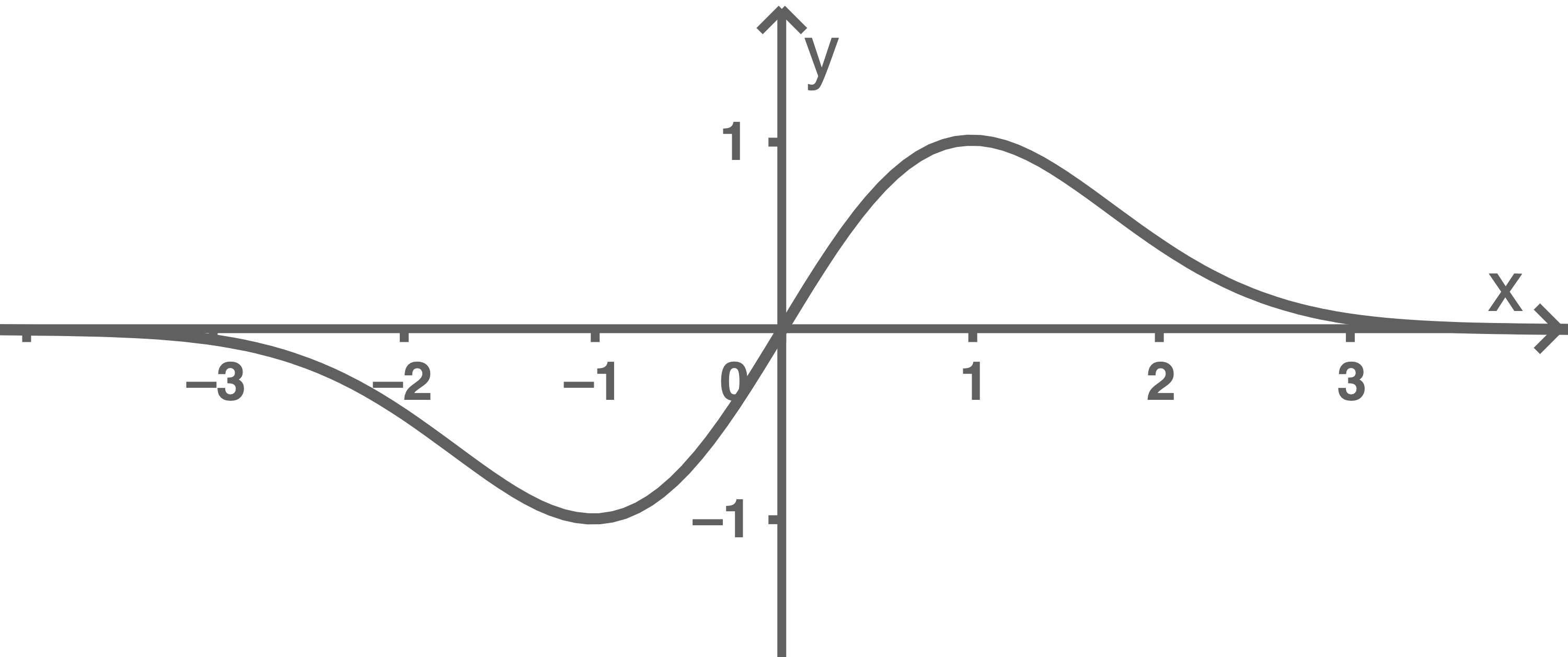
Abbildung 1 zeigt den Graphen von ohne das zugrunde liegende Koordinatensystem.
ohne das zugrunde liegende Koordinatensystem.
Ergänze die Koordinatenachsen und skaliere diese passend.

Abbildung 1 zeigt den Graphen von
Ergänze die Koordinatenachsen und skaliere diese passend.

Abb. 1
(5 BE)
b)
Interpretiere den folgenden Sachverhalt geometrisch:
Für jede Stammfunktion von
von  und für jede reele Zahl
und für jede reele Zahl  gilt:
gilt:

Für jede Stammfunktion
(3 BE)
c)
Begründe unter Verwendung der Abbildung 2, dass gilt:


Abb. 2
(3 BE)
d)
Für einen Wert von  liegt der Punkt
liegt der Punkt  auf dem Graphen von
auf dem Graphen von 
Berechne für diesen Wert von die Größe des Winkels, den der Graph von
die Größe des Winkels, den der Graph von  mit der Parallele zur
mit der Parallele zur  -Achse durch den Punkt
-Achse durch den Punkt  einschließt.
einschließt.
Berechne für diesen Wert von
(4 BE)
e)
Die folgenden Aussagen gelten für alle reellen Zahlen  und
und 
gilt genau dann, wenn
oder
ist.
(2 BE)
f)
Für alle Werte von  stimmen die Wendestellen von
stimmen die Wendestellen von  mit den Lösungen der Gleichung
mit den Lösungen der Gleichung  überein. Es ist
überein. Es ist  Klassifiziere die Anzahl der Wendestellen von
Klassifiziere die Anzahl der Wendestellen von  nach dem Wert von
nach dem Wert von 
(7 BE)
g)
Zeige, dass die folgende Aussage für jeden Wert von  richtig ist:
richtig ist:
Wird der Graph von mit dem gleichen Faktor
mit dem gleichen Faktor  sowohl in
sowohl in  -Richtung als auch in
-Richtung als auch in  -Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.
-Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.
Wird der Graph von
(4 BE)
h)
Beschreibe die Lage der Punkte  mit
mit  im Koordinatensystem und begründe, dass keiner dieser Punkte auf einem Graphen der Schar liegt.
im Koordinatensystem und begründe, dass keiner dieser Punkte auf einem Graphen der Schar liegt.
(4 BE)
i)
Alle Extrempunkte der Graphen der Schar liegen auf einer Geraden.
Begründe, dass es sich dabei um die Gerade mit der Gleichung handelt.
handelt.
Begründe, dass es sich dabei um die Gerade mit der Gleichung
(3 BE)
j)
Für jeden positiven Wert von  bilden der Hochpunkt
bilden der Hochpunkt  des Graphen von
des Graphen von  der Punkt
der Punkt  der Koordinatenursprung und der Punkt
der Koordinatenursprung und der Punkt  die Eckpunkte eines Vierecks.
die Eckpunkte eines Vierecks.
Bestimme ausgehend von einer Skizze denjenigen Wert von für den das Viereck den Flächeninhalt
für den das Viereck den Flächeninhalt  hat.
hat.
Bestimme ausgehend von einer Skizze denjenigen Wert von
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
1. Berechnung der Nullstellen
![\(\begin{array}[t]{rll}
f_1(x)&=& 0 \\[5pt]
x \cdot \mathrm{e}^{-\frac{1}{2}x^2+\frac{1}{2}} &=& 0
\end{array}\)](https://mathjax.schullv.de/3211557289dd62eb4f1e416820e64c2f2a1e6cadcd10c3bfde14cb73394f7503?color=5a5a5a) Da
Da  für alle
für alle  folgt mit dem Satz vom Nullprodukt, dass
folgt mit dem Satz vom Nullprodukt, dass  sein muss und dass dies die einzige Nullstelle ist.
2. Zeichnen des Koordinatensystems
Nach Aufgabenstellung ist der Graph von
sein muss und dass dies die einzige Nullstelle ist.
2. Zeichnen des Koordinatensystems
Nach Aufgabenstellung ist der Graph von  symmetrisch bezüglich des Koordinatenursprungs. Folgich muss der Koordinatenursprung im Wendepunkt des Graphen von
symmetrisch bezüglich des Koordinatenursprungs. Folgich muss der Koordinatenursprung im Wendepunkt des Graphen von  liegen. Mit dem GTR werden die Koordinaten des Hoch- und Tiefpunktes bestimmt: Tiefpunkt
liegen. Mit dem GTR werden die Koordinaten des Hoch- und Tiefpunktes bestimmt: Tiefpunkt  Hochpunkt
Hochpunkt 

b)
Nach Aufgabenstellung gilt für 
![\(\begin{array}[t]{rll}
F_1(u)-F_1(0)&\approx& \displaystyle\int_{0}^{2022}f_1(x)\;\mathrm dx \\[5pt]
\displaystyle\int_{0}^{u}f_1(x)\;\mathrm dx &\approx& \displaystyle\int_{0}^{2022}f_1(x)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/de415dcd056cd95b1417fb0730ef6e4aed00dd46bd8b56a564c80fabb4da48c1?color=5a5a5a) Für jede reelle Zahl
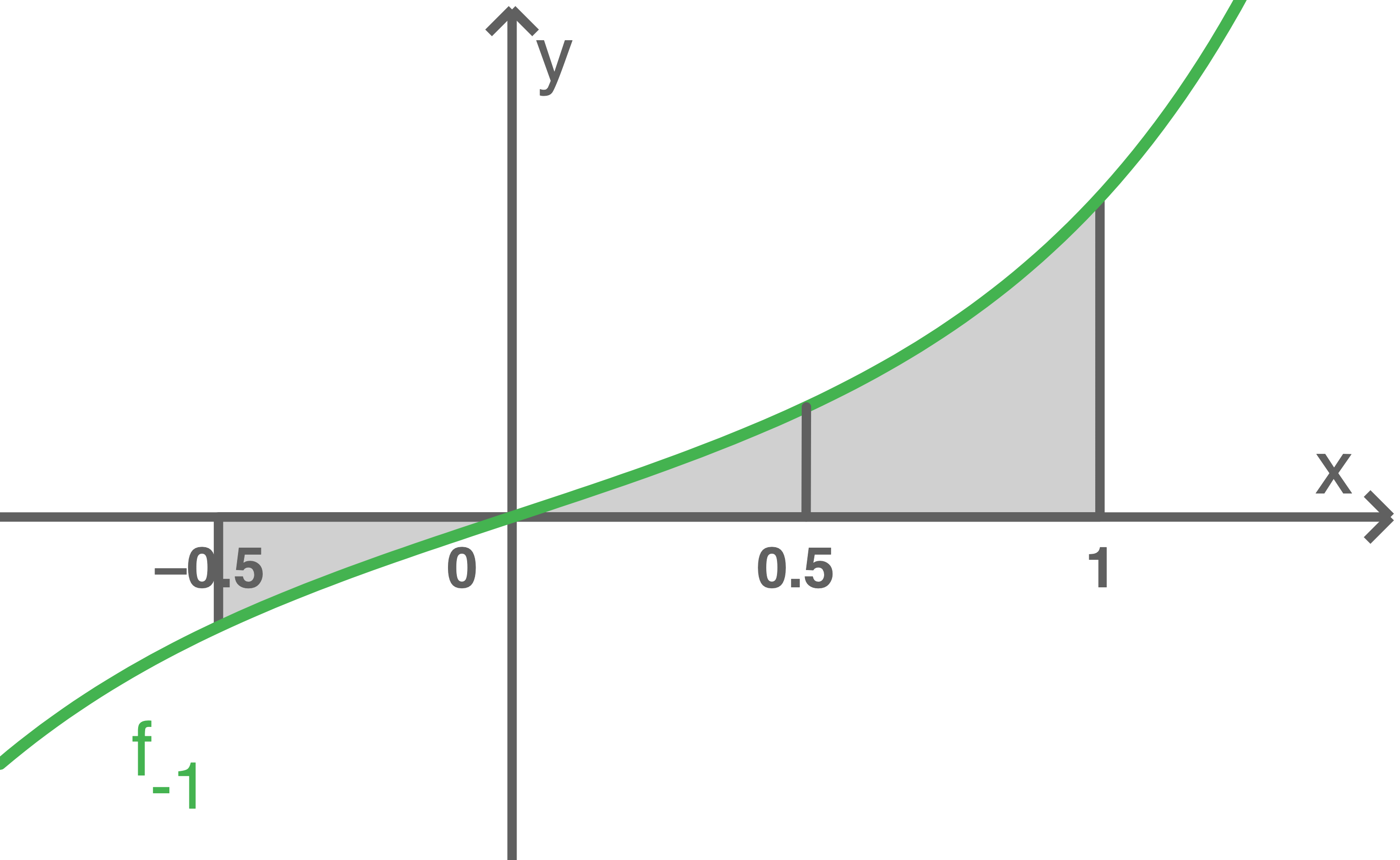
Für jede reelle Zahl  schließen der Graph von
schließen der Graph von  , die
, die  -Achse und die Gerade zu
-Achse und die Gerade zu  ein Flächenstück ein. Dessen Inhalt stimmt ungefähr mit dem Inhalt des Flächenstücks überein, das der Graph von
ein Flächenstück ein. Dessen Inhalt stimmt ungefähr mit dem Inhalt des Flächenstücks überein, das der Graph von  , die
, die  -Achse und die Gerade zu
-Achse und die Gerade zu  einschließen.
einschließen.
c)
Die beiden Teilflächen, die der Graph von  mit der
mit der  -Achse und den Geraden zu
-Achse und den Geraden zu  und
und  einschließt, haben den gleichen Inhalt, da
einschließt, haben den gleichen Inhalt, da  symmetrisch bezüglich des Koordinatenursprungs ist. Diese liegen auf unterschiedlichen Seiten der
symmetrisch bezüglich des Koordinatenursprungs ist. Diese liegen auf unterschiedlichen Seiten der  -Achse. Also heben sich die Integrale gegenseitig auf und es bleibt nur der Inhalt der Teilfläche im Intervall
-Achse. Also heben sich die Integrale gegenseitig auf und es bleibt nur der Inhalt der Teilfläche im Intervall ![\([0,5 ; 1]\)](https://mathjax.schullv.de/6d546ec166a63b35e8d3e4c9bb594302b1c601e96a119ce1039c147b45931df1?color=5a5a5a) übrig.
übrig.
d)
e)
- Alle Graphen der Schar schneiden sich im Koordinatenursprung.
- Keiner der Graphen hat einen weiteren Punkt mit einem anderen Graphen der Schar gemeinsam.
f)
Betrachtung von  Für
Für  hat der Graph keine Wendestelle, da
hat der Graph keine Wendestelle, da  und
und  gilt. Somit liegt im Graph von
gilt. Somit liegt im Graph von  keine Extremstellen vor und folglich treten im Graphen von
keine Extremstellen vor und folglich treten im Graphen von  keine Wendestellen auf.
Betrachtung von
keine Wendestellen auf.
Betrachtung von  Für
Für  sind die Wendestellen des Graphen von
sind die Wendestellen des Graphen von  gegeben durch folgenden Gleichung:
gegeben durch folgenden Gleichung:
![\(\begin{array}[t]{rll}
(a \cdot x^2-3)\cdot x&=& 0
\end{array}\)](https://mathjax.schullv.de/02e54ed469f0d639b828fa45fdc2ccab9dd60d537ccbe1d15f873e5f2ada9868?color=5a5a5a) Satz vom Nullprodukt: Es folgt
Satz vom Nullprodukt: Es folgt  oder
oder
![\(\begin{array}[t]{rll}
a \cdot x^2-3&=& 0&\quad \scriptsize \mid\; +3 \\[5pt]
a \cdot x^2&=& 3&\quad \scriptsize \mid\; :a \\[5pt]
x^2&=& \dfrac{3}{a} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/990024f46272ae198a959418d74526430adbc38feeddeb8b5611b2960877e7e0?color=5a5a5a) Für
Für  ist die Gleichung lösbar und es folgt
ist die Gleichung lösbar und es folgt  Für
Für  hat der Graph von
hat der Graph von  somit 3 Wendestellen, nämlich
somit 3 Wendestellen, nämlich  und
und  .
Für
.
Für  hat die Gleichung genau eine Lösung und der Graph von
hat die Gleichung genau eine Lösung und der Graph von  somit eine Wendestelle
somit eine Wendestelle 
g)
h)
Die Punkte  mit
mit  liegen im Inneren des zweiten und vierten Quadranten.
Für alle
liegen im Inneren des zweiten und vierten Quadranten.
Für alle  gilt
gilt  . Daraus folgt für
. Daraus folgt für  dass
dass  ist und für
ist und für  dass
dass  ist. Die Graphen der Schar liegen somit im Inneren des ersten bzw. dritten Quadranten.
ist. Die Graphen der Schar liegen somit im Inneren des ersten bzw. dritten Quadranten.
i)
Nach Aufgabenstellung liegen alle Extrempunkte auf einer Geraden. In Teilaufgabe a) wurde bereits gezeigt, dass der Graph von  die Extrempunkte
die Extrempunkte  und
und  hat. Folglich muss die Gerade durch den Funktionsterm
hat. Folglich muss die Gerade durch den Funktionsterm  beschrieben werden.
beschrieben werden.
j)
Für den Flächeninhalt gilt:
![\(\begin{array}[t]{rll}
A&=& 144 \\[5pt]
v^2 + \dfrac{1}{2} (2-v) \cdot v &=& 144 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2ed9ac010bb3b21d0f3b673698d65cfe0c700d5ee1ccea00e025862b86665f00?color=5a5a5a) Mit dem solve-Befehl des Taschenrechners folgt
Mit dem solve-Befehl des Taschenrechners folgt 
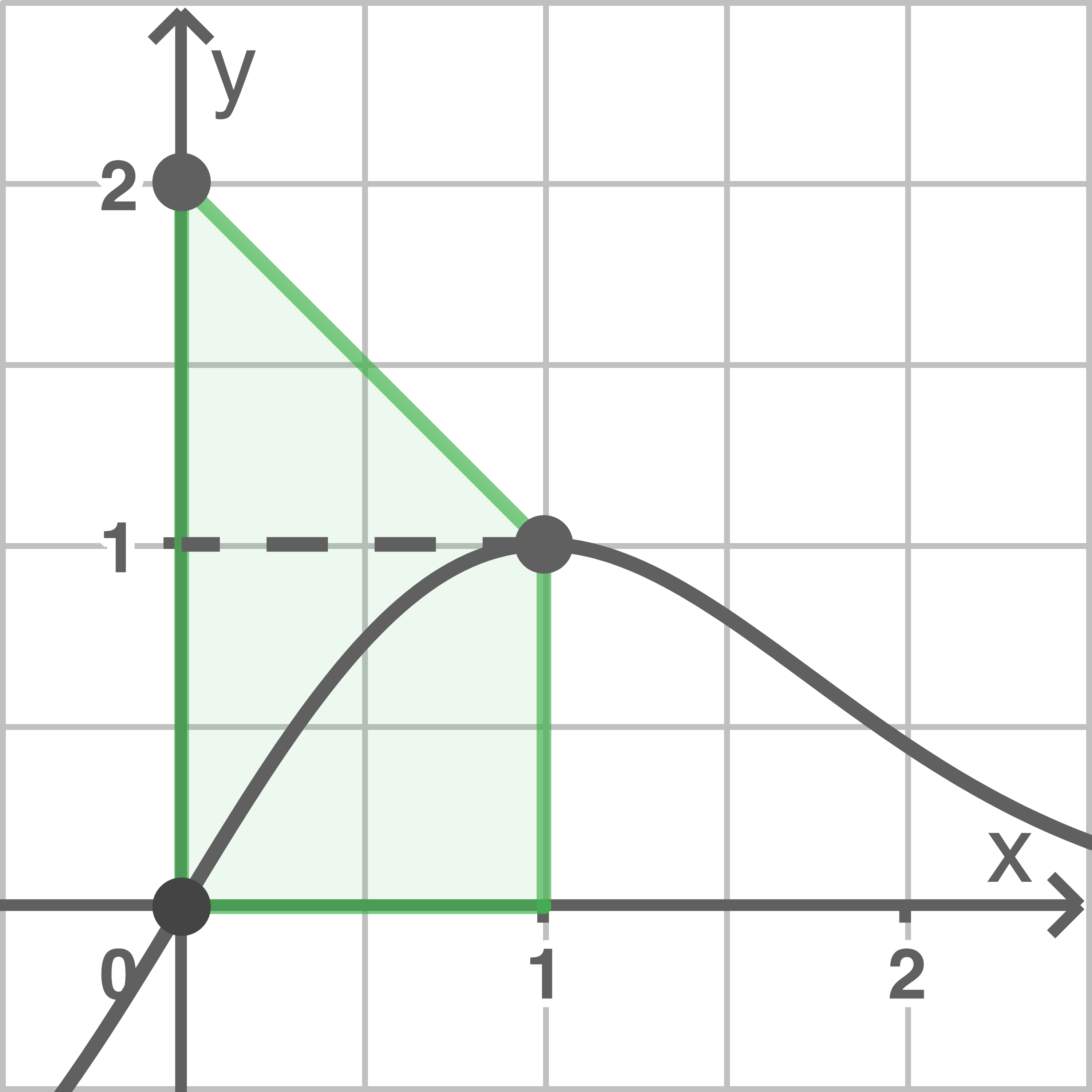
Skizze für  und
und 