Aufgabe 2A

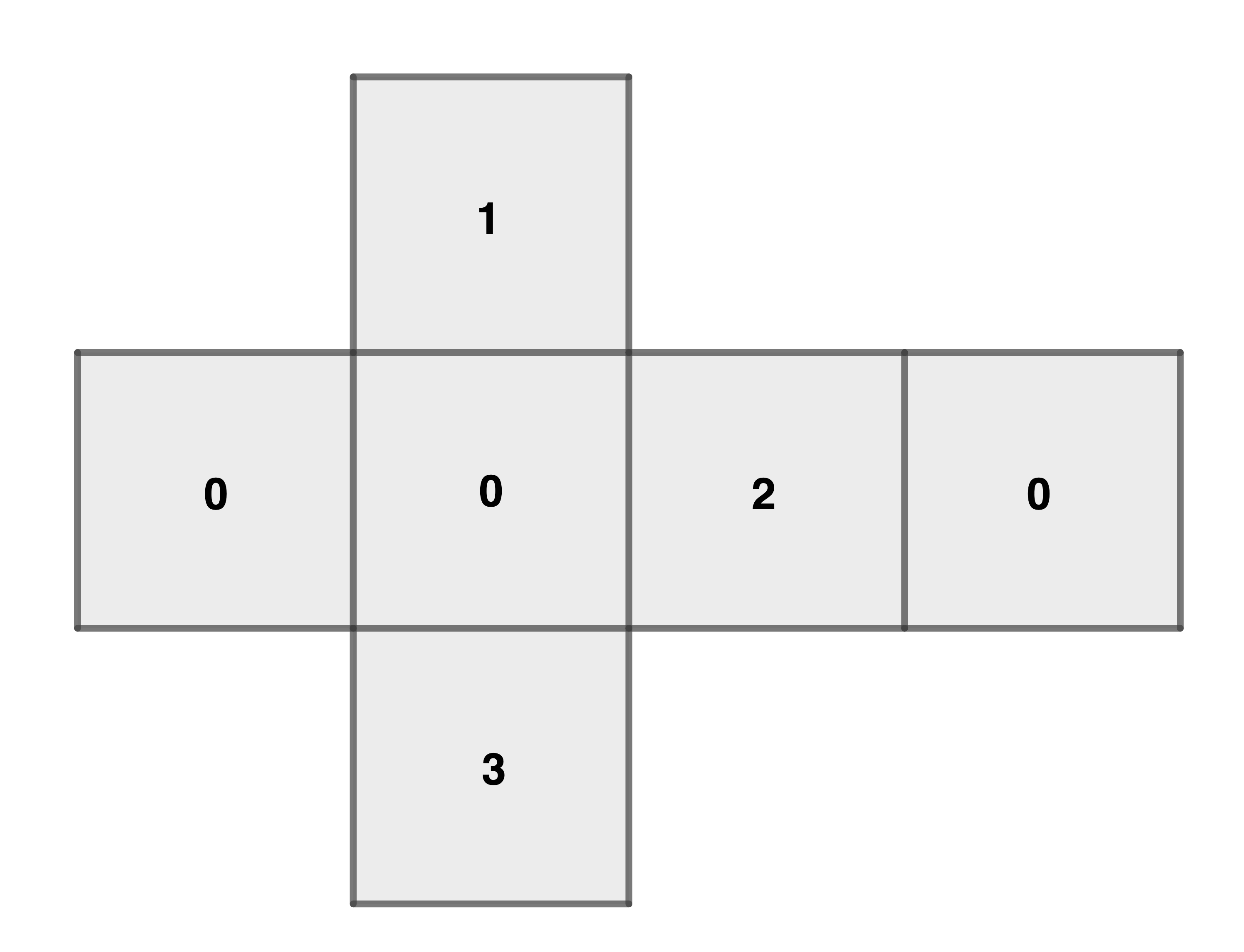
Ein Würfelspiel wird mit einem Würfel gespielt, dessen Netz in der nebenstehenden Abbildung dargestellt ist.
Der Spieler zahlt einen Einsatz von $5\,€$ und würfelt dann einmal. Anschließend wird ihm die Summe aller $5$ sichtbaren Zahlen in $\,€$ ausgezahlt.

Diagramm mit Zahlen in Kästchen, angeordnet in einer kreuzförmigen Struktur.

Die Zufallsgröße $X$ beschreibt den Betrag in $\,€$ , der an den Spieler ausgezahlt wird.
Begründe, dass $X$ nur die Werte $3, 4, 5$ und $6$ annehmen kann.
Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von $X$ .

$k$	$P(X=k)$
$3$	$\dfrac{1}{6}$
$4$	$\dfrac{1}{6}$
$5$	$\dfrac{1}{6}$
$6$	$\dfrac{1}{2}$

Gib ein Ereignis an, das bezüglich dieser Verteilung mit einer Wahrscheinlichkeit von $\dfrac{2}{3}$ eintritt.
Ein Spiel heißt fair, wenn die Einsätze und die Auszahlungen auf lange Sicht ausgeglichen sind.
Zeige, dass das Spiel fair ist.
Berechne den Zahlenwert, mit dem eine der drei $"0"$ -Seitenflächen des Würfels überklebt werden muss, damit das Spiel bei einem Einsatz von $7,50 \,€$ fair ist.

(12 BE)

Es wird $10$ -mal mit dem oben abgebildeten Würfel gespielt. Die Zufallsgröße $Y$ beschreibt die Anzahl der Spiele, bei denen $6 \,€$ ausgezahlt werden.

Berechne die Wahrscheinlichkeit dafür, dass

bei mindestens $3$ Spielen $6 \,€$ ausgezahlt werden,
bei höchstens $6$ Spielen weniger als $6 \,€$ ausgezahlt werden.

Begründe ohne Berechnung der Wahrscheinlichkeiten, dass $P(Y = 3) =P(Y = 7)$ gilt.

Erläutere, dass der Term $\dfrac{1}{3}\cdot P(Y=9)$ die Wahrscheinlichkeit dafür angibt, dass bei den $10$ Spielen insgesamt $59\,€$ ausgezahlt werden.

(12 BE)

$X$ : Betrag in $€$ , der an den Spieler ausgezahlt wird.

Werte für $X$ bestimmen:

Wird der Würfel geworfen, wird dem Spieler die Summer aller fünf sichtbaren Zahlen ausgezahlt.
Ist eine $0$ nicht sichtbar, beträgt die Auszahlungssumme $0+0+1+2+3=6\,€$ , ist die $1$ nicht sichtbar, beträgt die Auszahlungssumme $0+0+0+2+3=5\,€$ , ist die $2$ nicht sichtbar, beträgt die Auszahlungssumme $0+0+0+1+3=4\,€$ und liegt die $3$ unten, beträgt die Auszahlungssumme $0+0+0+1+2=3\,€$ .

Daraus folgt, dass $X$ nur die Werte $3$ , $4$ , $5$ und $6$ annehmen kann.

Mögliches Ereignis angeben:

$A:$ ein gerader Betrag wird ausgezahlt

$\begin{array}[t]{rll} P(A)&=&P(X=4)+P(X=6) &\quad \\[5pt] &=&\dfrac{1}{6}+\dfrac{1}{2} \\[5pt] &=&\dfrac{2}{3} \end{array}$

Erwartungswert bestimmen:

Damit das Spiel fair ist, muss für den Erwartungswert $E(X)=5$ gelten, sodass sich die Einsätze und die Auszahlungen ausgleichen.

$E(x)= \dfrac{1}{6} \cdot 3 +\dfrac{1}{6} \cdot 4 + \dfrac{1}{6} \cdot 5 + \dfrac{1}{2} \cdot 6 = 5$

Der Erwartungswert des ausgezahlten Betrags ist gleich dem eingezahlten Betrag und somit ist das Spiel fair.

Neuer Zahlenwert $a$ bestimmen:

Wird eine der drei " $0$ "-Seitenflächen des Würfels überklebt, ist die Wahrscheinlichkeit eine $0$ zu würfeln nur noch $\dfrac{2}{6}$ groß und es kommt eine neue Wahrscheinlichkeit von $\dfrac{1}{6}$ dazu.

Damit das Spiel fair ist, muss für den Erwartungswert $E(X)=7,50$ gelten, sodass sich die Einsätze und die Auszahlungen ausgleichen.

Der Parameter $a$ beschreibt den gesuchten Zahlenwert.

$k$	$P(X=k)$
$3+a$	$\dfrac{1}{6}$
$4+a$	$\dfrac{1}{6}$
$5+a$	$\dfrac{1}{6}$
$6+a$	$\dfrac{2}{6}$
$6$	$\dfrac{1}{6}$

$E(X)=7,5$

$a=3$

Vollständige Lösung anzeigen

Eine der drei " $0$ "-Seitenfläche muss mit dem Zahlenwert $3$ überklebt werden, damit das Spiel bei einem Einsatz von $7,50\,€$ fair ist.

$Y$ : Anzahl der Spiele, bei denen $6\,€$ ausgezahlt werden

Die Zufallsgröße $Y$ kann mit $n=10$ und $p=0,5$ als binomialverteilt angenommen werden.

Wahrscheinlichkeiten berechnen:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ vars (distr) $\to$ B: binomcdf

$\blacktriangleright$ Casio fx-CG

Statistik: F5: DIST $\to$ F5: BINOM $\to$ F2: Bcd

Wahrscheinlichkeit dafür, dass bei mindestens $3$ Spielen $6\,€$ ausgezahlt werden:

$P(Y\geq 3)\approx 0,945$

Vollständige Lösung anzeigen

Wahrscheinlichkeit dafür, dass bei höchstens $6$ Spielen weniger als $6\,€$ ausgezahlt werden:

$P(Y\geq 4) \approx 0,828$

Vollständige Lösung anzeigen

$P(Y=3)=P(Y=7)$ begründen:

Die Wahrscheinlichkeitsverteilung der Zufallsgröße $Y$ ist wegen $p=0,5$ symmetrisch zu ihrem Erwartungswert $E(Y)= 10 \cdot \dfrac{1}{2} =5$ . Die Werte 3 und 7 liegen ebenfalls symmetrisch zu $E(Y)$ .

Bedeutung des Terms $\dfrac{1}{3}\cdot P(Y=9)$ erläutern:

In Summe werden $59\, €$ ausgezahlt, wenn bei $9$ Spielen $6\,€$ und bei einem Spiel $5\,€$ ausgezahlt werden. $P(Y=9)$ gibt die Wahrscheinlichkeit für $9$ Spiele mit einer Auszahlung von $6\,€$ an. Diese muss durch $3$ dividiert werden, da für das übrige Spiel $3$ gleichwahrscheinliche Ergebnisse möglich sind.