Aufgabe 1B
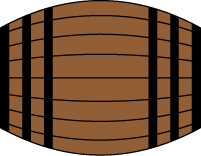
Ein Holzfass ist  hoch, hat in der Mitte einen Radius von
hoch, hat in der Mitte einen Radius von  und an Boden und Deckel den Radius
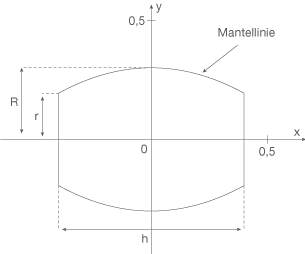
und an Boden und Deckel den Radius  . Das Fass wird entsprechend der Abbildung im Koordinatensystem symmetrisch zur
. Das Fass wird entsprechend der Abbildung im Koordinatensystem symmetrisch zur  -Achse liegend betrachtet.
-Achse liegend betrachtet.

a) Die Mantellinie kann näherungsweise mithilfe einer Parabel beschrieben werden. Bestimmen Sie für die Mantellinie des Fasses mit den oben genannten Maßen eine Gleichung der Funktion  mit
mit  ,
,  ,
,  .
Berechnen Sie damit das Rotationsvolumen des Fasses.
Johannes Kepler entwickelte die folgende Formel zur Berechnung des Volumens eines Fasses:
.
Berechnen Sie damit das Rotationsvolumen des Fasses.
Johannes Kepler entwickelte die folgende Formel zur Berechnung des Volumens eines Fasses:
 .
Vergleichen Sie Ihr Ergebnis für das Rotationsvolumen des Fasses mit dem Ergebnis, das Sie mithilfe der Keplerschen Fassformel erhalten.
.
Vergleichen Sie Ihr Ergebnis für das Rotationsvolumen des Fasses mit dem Ergebnis, das Sie mithilfe der Keplerschen Fassformel erhalten.

(11P)
Die Mantellinie des Fasses wird in einer anderen Modellierung für  beschrieben durch Funktionsgraphen der Schar
beschrieben durch Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  .
.
b) Begründen Sie, dass die Mantellinie für  beschrieben wird durch die Funktionsgraphen der Schar
beschrieben wird durch die Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  .
Die Graphen der Modellierungsfunktionen der Scharen
.
Die Graphen der Modellierungsfunktionen der Scharen  und
und  sollen die Wölbung des Fasses an der Stelle
sollen die Wölbung des Fasses an der Stelle  jeweils sprung-, knick- und krümmungsruckfrei beschreiben.
Zeigen Sie, dass diese Forderungen erfüllt werden, wenn gilt:
jeweils sprung-, knick- und krümmungsruckfrei beschreiben.
Zeigen Sie, dass diese Forderungen erfüllt werden, wenn gilt:  .
.
(13P)
Unabhängig vom Sachzusammenhang werden die Funktionen der Schar  nun für alle
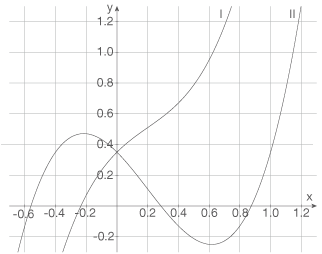
nun für alle  betrachtet. In der Anlage sind beispielhaft zwei Graphen der Schar
betrachtet. In der Anlage sind beispielhaft zwei Graphen der Schar  dargestellt.
Betrachtet werden im Folgenden auch die Tangenten
dargestellt.
Betrachtet werden im Folgenden auch die Tangenten  an die Graphen der Schar
an die Graphen der Schar  an der Stelle
an der Stelle  .
.
c) Bestimmen Sie die Gleichung dieser Tangenten  .
(Zur Kontrolle:
.
(Zur Kontrolle:  )
Entscheiden Sie mithilfe des Verhaltens der Funktionsgraphen an der Stelle
)
Entscheiden Sie mithilfe des Verhaltens der Funktionsgraphen an der Stelle  , welcher der Graphen in der Anlage zu einer Funktion mit positivem Parameter
, welcher der Graphen in der Anlage zu einer Funktion mit positivem Parameter  gehört.
gehört.
(9P)
d) Die Graphen der Funktionenschar  haben mit den jeweils zugehörigen Tangenten
haben mit den jeweils zugehörigen Tangenten  die Punkte
die Punkte  und
und  gemeinsam.
Bestimmen Sie den Parameter
gemeinsam.
Bestimmen Sie den Parameter  so, dass die Punkte
so, dass die Punkte  und
und  den kleinsten Abstand voneinander haben.
Untersuchen Sie, ob der Inhalt der Fläche, die von jedem Graphen und der zugehörigen Tangente
den kleinsten Abstand voneinander haben.
Untersuchen Sie, ob der Inhalt der Fläche, die von jedem Graphen und der zugehörigen Tangente  eingeschlossen wird, vom Parameter
eingeschlossen wird, vom Parameter  abhängig ist.
abhängig ist.
(13P)
(46P)
Material
Anlage: Graphen zu Teilaufgabe c)
a)  Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion
Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion  mit
mit  ,
,  ,
,  .
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
.
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
 und
und  Setze
Setze  in
in  ein:
ein:
 Es gilt
Es gilt  . Setze
. Setze  und
und  in
in  ein:
ein:
 Es gilt
Es gilt  . Die Gleichung von
. Die Gleichung von  ist somit gegeben durch
ist somit gegeben durch  .
.
 Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
 Die Grenzen des Integrals sind gegeben durch
Die Grenzen des Integrals sind gegeben durch  und
und  .
.
 Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von
Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von  zeichnen lässt und folgendermaßen vorgehst:
zeichnen lässt und folgendermaßen vorgehst:
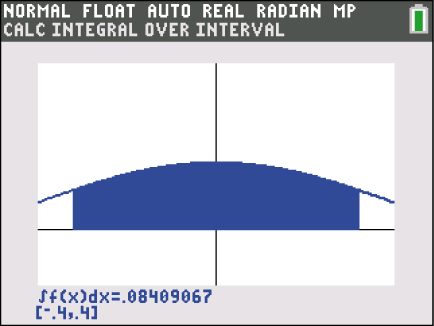 Der Wert des Integrals ist
Der Wert des Integrals ist  . Für das Volumen ergibt sich also:
. Für das Volumen ergibt sich also:
 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
.
 Keplersche Fassformel
Die Keplersche Fassformel lautet:
Keplersche Fassformel
Die Keplersche Fassformel lautet:
 .
Du sollst damit das Volumen des Fasses berechnen:
.
Du sollst damit das Volumen des Fasses berechnen:
 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
Die Berechnungen liefern die gleichen Volumina.
.
Die Berechnungen liefern die gleichen Volumina.
2nd  TRACE (CALC)
TRACE (CALC)  7:
7: 

b)  Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für
Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für  beschrieben wird durch die Funktionsgraphen der Schar
beschrieben wird durch die Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  . Die Mantellinie ist symmetrisch zur
. Die Mantellinie ist symmetrisch zur  -Achse, also muss
-Achse, also muss  gelten, damit diese Funktionen die Mantellinie beschreiben.
gelten, damit diese Funktionen die Mantellinie beschreiben.
 Die Bedingung ist erfüllt, also wird die Mantellinie für
Die Bedingung ist erfüllt, also wird die Mantellinie für  beschrieben durch die Funktionsgraphen der Schar
beschrieben durch die Funktionsgraphen der Schar  .
.
 Übergang der beiden Funktionen
Damit der Übergang an der Stelle
Übergang der beiden Funktionen
Damit der Übergang an der Stelle  jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
 Überprüfe die Bedingungen:
Überprüfe die Bedingungen:
 erfüllt.
Für
erfüllt.
Für  ist der Übergang sprung-, knick- und krümmungsruckfrei.
ist der Übergang sprung-, knick- und krümmungsruckfrei.
und
- Also muss gelten:
c)  Bestimme die Gleichung der Tangenten
Bestimme die Gleichung der Tangenten  Die Ableitung der Funktionenschar hast du im Aufgabenteil b) berechnet:
Die Ableitung der Funktionenschar hast du im Aufgabenteil b) berechnet:
 Du kannst dann die Steigung der Tangente berechnen:
Du kannst dann die Steigung der Tangente berechnen:
 Der
Der  -Achsenabschnitt ist gegeben durch
-Achsenabschnitt ist gegeben durch  . Die Gleichung der Tangente ist dann gegeben durch:
. Die Gleichung der Tangente ist dann gegeben durch:

 Funktion mit positivem Parameter
Funktion mit positivem Parameter  Der Parameter
Der Parameter  entspricht der Steigung der Tangente an der Stelle
entspricht der Steigung der Tangente an der Stelle  . Die Funktion mit positivem Parameter
. Die Funktion mit positivem Parameter  ist also die Funktion, deren Graph eine positive Steigung an der Stelle
ist also die Funktion, deren Graph eine positive Steigung an der Stelle  hat. Das ist Graph I.
hat. Das ist Graph I.
d)  Kleinster Abstand zwischen
Kleinster Abstand zwischen  und
und  Die Graphen der Funktionenschar
Die Graphen der Funktionenschar  haben mit den jeweils zugehörigen Tangenten
haben mit den jeweils zugehörigen Tangenten  die Punkte
die Punkte  und
und  gemeinsam. Du sollst
gemeinsam. Du sollst  so bestimmen, dass die Punkte
so bestimmen, dass die Punkte  und
und  den kleinsten Abstand voneinander haben. Berechne zuerst die
den kleinsten Abstand voneinander haben. Berechne zuerst die  -Koordinaten der Punkte:
-Koordinaten der Punkte:
 und
und  Die kürzeste Entfernung haben die beiden Punkte, wenn sie durch eine waagrechte Tangente verbunden sind. Das ist der Fall, wenn die
Die kürzeste Entfernung haben die beiden Punkte, wenn sie durch eine waagrechte Tangente verbunden sind. Das ist der Fall, wenn die  -Koordinaten der Punkte übereinstimmen:
-Koordinaten der Punkte übereinstimmen:
 Alternativ
Du kannst den Parameter mit dem kleinsten Abstand auch durch Minimieren der folgenden Formel bestimmen:
Alternativ
Du kannst den Parameter mit dem kleinsten Abstand auch durch Minimieren der folgenden Formel bestimmen:
 Durch Einsetzen der Koordinaten erhältst du:
Durch Einsetzen der Koordinaten erhältst du:
 Minimiere diese Funktion mithilfe deines Taschenrechners.
Minimiere diese Funktion mithilfe deines Taschenrechners.
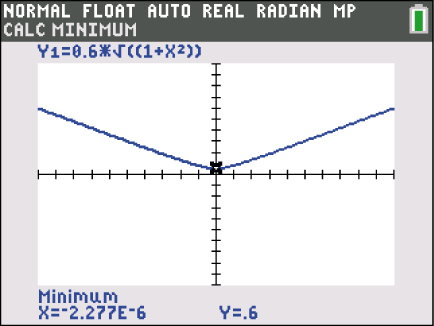 Für
Für  ist der Abstand zwischen
ist der Abstand zwischen  und
und  am kleinsten.
am kleinsten.
 Abhängigkeit des Flächeninhalts vom Parameter
Abhängigkeit des Flächeninhalts vom Parameter  untersuchen
Untersuche, ob der Inhalt der Fläche, die von jedem Graphen und der zugehörigen Tangente
untersuchen
Untersuche, ob der Inhalt der Fläche, die von jedem Graphen und der zugehörigen Tangente  eingeschlossen wird, vom Parameter
eingeschlossen wird, vom Parameter  abhängig ist. Die Schnittstellen der Tangenten und der Graphen der Funktionenschar sind
abhängig ist. Die Schnittstellen der Tangenten und der Graphen der Funktionenschar sind  und
und  . Du hast also folgendes Integral:
. Du hast also folgendes Integral:
 Sowohl die Integralgrenzen, als auch der Integrand sind von
Sowohl die Integralgrenzen, als auch der Integrand sind von  unabhängig, somit ist auch der Inhalt der Fläche unabhängig vom Parameter
unabhängig, somit ist auch der Inhalt der Fläche unabhängig vom Parameter  .
Alternativ
Du kannst das auch feststellen, indem du das Integral berechnest.
.
Alternativ
Du kannst das auch feststellen, indem du das Integral berechnest.
![\(\begin{array}{rcll}
\displaystyle\int_{0}^{0,6} t_k - f_k(x) \mathrm dx&=&\displaystyle\int_{0}^{0,6} - 2,5\cdot x^3 +1,5\cdot x^2 \mathrm dx&\\
&=&\left[-\frac{5}{8}x^4 + 0,5 \cdot x^3\right]_0^{0,6}&\\
&=&0,027&
\end{array}\)](https://mathjax.schullv.de/f003945bed3b69fdccb04de04b802f2c5ec402cb7b37a6650096516984f08531?color=5a5a5a) Das Ergebnis enthält kein
Das Ergebnis enthält kein  , der Inhalt der Fläche ist also unabhängig vom Parameter
, der Inhalt der Fläche ist also unabhängig vom Parameter  .
.
2nd  TRACE (CALC)
TRACE (CALC)  3: minimum
3: minimum

a)  Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion
Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion  mit
mit  ,
,  ,
,  .
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
.
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
 und
und  Setze
Setze  in
in  ein:
ein:
 Es gilt
Es gilt  . Setze
. Setze  und
und  in
in  ein:
ein:
 Es gilt
Es gilt  . Die Gleichung von
. Die Gleichung von  ist somit gegeben durch
ist somit gegeben durch  .
.
 Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
 Die Grenzen des Integrals sind gegeben durch
Die Grenzen des Integrals sind gegeben durch  und
und  .
.
 Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von
Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von  zeichnen lässt und folgendermaßen vorgehst:
zeichnen lässt und folgendermaßen vorgehst:
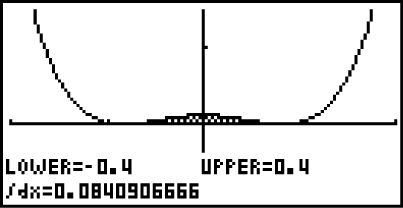 Der Wert des Integrals ist
Der Wert des Integrals ist  . Für das Volumen ergibt sich also:
. Für das Volumen ergibt sich also:
 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
.
 Keplersche Fassformel
Die Keplersche Fassformel lautet:
Keplersche Fassformel
Die Keplersche Fassformel lautet:
 .
Du sollst damit das Volumen des Fasses berechnen:
.
Du sollst damit das Volumen des Fasses berechnen:
 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
Die Berechnungen liefern die gleichen Volumina.
.
Die Berechnungen liefern die gleichen Volumina.
F5: G-Solv  F6
F6  F3
F3

b)  Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für
Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für  beschrieben wird durch die Funktionsgraphen der Schar
beschrieben wird durch die Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  . Die Mantellinie ist symmetrisch zur
. Die Mantellinie ist symmetrisch zur  -Achse, also muss
-Achse, also muss  gelten, damit diese Funktionen die Mantellinie beschreiben.
gelten, damit diese Funktionen die Mantellinie beschreiben.
 Die Bedingung ist erfüllt, also wird die Mantellinie für
Die Bedingung ist erfüllt, also wird die Mantellinie für  beschrieben durch die Funktionsgraphen der Schar
beschrieben durch die Funktionsgraphen der Schar  .
.
 Übergang der beiden Funktionen
Damit der Übergang an der Stelle
Übergang der beiden Funktionen
Damit der Übergang an der Stelle  jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
 Überprüfe die Bedingungen:
Überprüfe die Bedingungen:
 erfüllt.
Für
erfüllt.
Für  ist der Übergang sprung-, knick- und krümmungsruckfrei.
ist der Übergang sprung-, knick- und krümmungsruckfrei.
und
- Also muss gelten:
c)  Bestimme die Gleichung der Tangenten
Bestimme die Gleichung der Tangenten  Die Ableitung der Funktionenschar hast du im Aufgabenteil b) berechnet:
Die Ableitung der Funktionenschar hast du im Aufgabenteil b) berechnet:
 Du kannst dann die Steigung der Tangente berechnen:
Du kannst dann die Steigung der Tangente berechnen:
 Der
Der  -Achsenabschnitt ist gegeben durch
-Achsenabschnitt ist gegeben durch  . Die Gleichung der Tangente ist dann gegeben durch:
. Die Gleichung der Tangente ist dann gegeben durch:

 Funktion mit positivem Parameter
Funktion mit positivem Parameter  Der Parameter
Der Parameter  entspricht der Steigung der Tangente an der Stelle
entspricht der Steigung der Tangente an der Stelle  . Die Funktion mit positivem Parameter
. Die Funktion mit positivem Parameter  ist also die Funktion, deren Graph eine positive Steigung an der Stelle
ist also die Funktion, deren Graph eine positive Steigung an der Stelle  hat. Das ist Graph I.
hat. Das ist Graph I.
d)  Kleinster Abstand zwischen
Kleinster Abstand zwischen  und
und  Die Graphen der Funktionenschar
Die Graphen der Funktionenschar  haben mit den jeweils zugehörigen Tangenten
haben mit den jeweils zugehörigen Tangenten  die Punkte
die Punkte  und
und  gemeinsam. Du sollst
gemeinsam. Du sollst  so bestimmen, dass die Punkte
so bestimmen, dass die Punkte  und
und  den kleinsten Abstand voneinander haben. Berechne zuerst die
den kleinsten Abstand voneinander haben. Berechne zuerst die  -Koordinaten der Punkte:
-Koordinaten der Punkte:
 und
und  Die kürzeste Entfernung haben die beiden Punkte, wenn sie durch eine waagrechte Tangente verbunden sind. Das ist der Fall, wenn die
Die kürzeste Entfernung haben die beiden Punkte, wenn sie durch eine waagrechte Tangente verbunden sind. Das ist der Fall, wenn die  -Koordinaten der Punkte übereinstimmen:
-Koordinaten der Punkte übereinstimmen:
 Alternativ
Du kannst den Parameter mit dem kleinsten Abstand auch durch Minimieren der folgenden Formel bestimmen:
Alternativ
Du kannst den Parameter mit dem kleinsten Abstand auch durch Minimieren der folgenden Formel bestimmen:
 Durch Einsetzen der Koordinaten erhältst du:
Durch Einsetzen der Koordinaten erhältst du:
 Minimiere diese Funktion mithilfe deines Taschenrechners.
Minimiere diese Funktion mithilfe deines Taschenrechners.
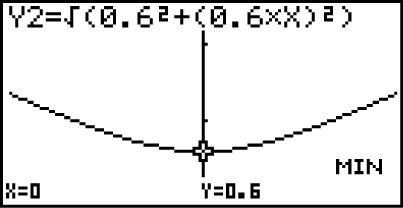 Für
Für  ist der Abstand zwischen
ist der Abstand zwischen  und
und  am kleinsten.
am kleinsten.
 Abhängigkeit des Flächeninhalts vom Parameter
Abhängigkeit des Flächeninhalts vom Parameter  untersuchen
Untersuche, ob der Inhalt der Fläche, die von jedem Graphen und der zugehörigen Tangente
untersuchen
Untersuche, ob der Inhalt der Fläche, die von jedem Graphen und der zugehörigen Tangente  eingeschlossen wird, vom Parameter
eingeschlossen wird, vom Parameter  abhängig ist. Die Schnittstellen der Tangenten und der Graphen der Funktionenschar sind
abhängig ist. Die Schnittstellen der Tangenten und der Graphen der Funktionenschar sind  und
und  . Du hast also folgendes Integral:
. Du hast also folgendes Integral:
 Sowohl die Integralgrenzen, als auch der Integrand sind von
Sowohl die Integralgrenzen, als auch der Integrand sind von  unabhängig, somit ist auch der Inhalt der Fläche unabhängig vom Parameter
unabhängig, somit ist auch der Inhalt der Fläche unabhängig vom Parameter  .
Alternativ
Du kannst das auch feststellen, indem du das Integral berechnest.
.
Alternativ
Du kannst das auch feststellen, indem du das Integral berechnest.
![\(\begin{array}{rcll}
\displaystyle\int_{0}^{0,6} t_k - f_k(x) \mathrm dx&=&\displaystyle\int_{0}^{0,6} - 2,5\cdot x^3 +1,5\cdot x^2 \mathrm dx&\\
&=&\left[-\frac{5}{8}x^4 + 0,5 \cdot x^3\right]_0^{0,6}&\\
&=&0,027&
\end{array}\)](https://mathjax.schullv.de/f003945bed3b69fdccb04de04b802f2c5ec402cb7b37a6650096516984f08531?color=5a5a5a) Das Ergebnis enthält kein
Das Ergebnis enthält kein  , der Inhalt der Fläche ist also unabhängig vom Parameter
, der Inhalt der Fläche ist also unabhängig vom Parameter  .
.
F5: G-Solv  F3: MIN
F3: MIN
