Aufgabe P1
a)
 Nullstellen von
Nullstellen von  bestimmen
bestimmen
Um die Nullstellen der Funktion

zu bestimmen, setzt du die Funktion zunächst gleich null.
Die Funktion

ist ein
Produkt aus den zwei
Faktoren 
und

. Diese werden nach dem Satz des Nullprodukts genau dann null, wenn ein Faktor null wird.
Somit musst du bestimmen, für welche

die beiden Faktoren

und

null werden.
Da

laut Voraussetzung größer null ist, ist der erste Faktor genau dann null, wenn

ist.
Der zweite Faktor ist genau dann null, wenn

ist.
Somit hat die Funktion

die Nullstellen

und

.
b)
 Wert von
Wert von  bestimmen
bestimmen
Das Integral

soll

sein. Im ersten Schritt berechnest du das Integral

in Abhänigigkeit von

, um anschließend das Ergebnis mit

gleichzusetzen und

zu bestimmen.
1.Schritt: Integral berechnen
Das Integral

entspricht also

.
2.Schritt: Gleichsetzen
Um nun ein konkretes

zu berechnen, musst du das Ergebnis

mit den gegebenen

gleichsetzen.
![\(\begin{array}[t]{rll}
\dfrac{1}{6} a^4 &=& \dfrac{8}{3} &\quad \scriptsize \mid\ \cdot 6 \\[5pt]
a^4 &=& 16 &\quad \scriptsize \mid\ \sqrt{ \,} \\[5pt]
a^2 &=& 4 &\quad \scriptsize \mid\ \sqrt{ \,} \\[5pt]
a &=& \pm 2
\end{array}\)](https://mathjax.schullv.de/90af3ebba77bfb3fe30f82fd16e640a05c0fbb7fec84bb6a2ea0acaeb98664e5?color=5a5a5a)
Für

kommen also die Werte

und

infrage. Da aber laut Voraussetzung

eine
positive Zahl ist, muss

gleich

sein.
Aufgabe P2
a)
 Parameter für sprung- und knickfreie Funktion bestimmen
Parameter für sprung- und knickfreie Funktion bestimmen
In dieser Aufgabe hast du zwei Funktionsterme mit angrenzenden Definitionsbereichen gegeben. Du sollst einen Wert für den Parameter

des zweiten Funktionsterms

finden, sodass der Graph der ersten Funktion ohne Unterbrechung oder Knick in den der zweiten Funktion übergeht.
Die Voraussetzungen hierfür sind, dass die Funktionswerte und Steigungen am Übergang (

) gleich sind. Um dies zu überprüfen, bestimmst du zunächst die Funktions- und Steigungswerte von

für den parameterfreien Funktionsterm

.
Danach setzt du diese mit dem Funktionsterm mit Parameter

bzw. mit dessen Ableitung gleich.
1.Schritt: Funktions- und Steigunswerte von  bestimmen
bestimmen
Den Funktionswert von

an der Stelle

bestimmst du durch das Einsetzen von

in den Funktionsterm.

Danach bestimmst du den Steigungswert der Funktion an der gleichen Stelle. Dies kannst du mit der 1. Ableitung tun.
![\(\begin{array}[t]{rll}
f(x) &=& e^{x-1} &\quad \scriptsize \mid\;\text{ableiten} \\[5pt]
f](https://mathjax.schullv.de/301c91b24641e7741aaa9146979188aefe2e647bed58aa5a0a73a750b2cff10c?color=5a5a5a) 2.Schritt: Mögliche Werte für
2.Schritt: Mögliche Werte für  bestimmen
bestimmen
Den so bestimmten Funktionswert setzt du nun mit

gleich und bestimmst so mögliche Werte für den Parameter

.
![\(\begin{array}[t]{rll}
1 &=& g_a(1) &\quad \scriptsize \; \\[5pt]
1 &=& -1^2+a \cdot 1 -1 &\quad \scriptsize \; \\[5pt]
1 &=& -2 +a &\quad \scriptsize \mid\; +2\\[5pt]
3 &=& a &\quad \scriptsize \; \\[5pt]
\end{array}\)](https://mathjax.schullv.de/be3c775de0fbe39aaa9d356fa7612089a49552b605f16fe7d9d0e9ed206dd608?color=5a5a5a)
Den so gefundenen Wert setzt du nun als

in

ein und leitest diese Funktion einmal ab. Danach bestimmst du die Steigung des Graphen von

an der Stelle

. Ist die Steigung gleich 1, gibt es einen Wert, bei dem die Graphen knickfrei aneinander schließen.
Die Steigung des Graphen von

entspricht der Steigung von

an der Stelle

.
Für

schließt der Graph von

sowohl sprung- als auch knickfrei an

an.
b)
 Krümmungsruckfreien Übergang untersuchen
Krümmungsruckfreien Übergang untersuchen
Ein krümmungsruckfreier Übergang kann mit der zweiten Ableitung gezeigt werden. Der Funktionswert der zweiten Ableitung an der Übergangsstelle der beiden Funktionen muss gleich sein, um einen krümmungsruckfreien Übergang zu haben.
Eine Parabel ist immer eine Funktion in folgender Form:
Bei einer nach unten geöffneten Parabel ist

immer negativ. Leitest du eine solche Funktion zweimal ab besteht diese Ableitung nur noch aus einer negativen Zahl:
![\(\begin{array}[t]{rll}
h(x) &=& a \cdot x^2 + b \cdot x + c \\[5pt]
h](https://mathjax.schullv.de/a67fdfce64e397804683e7d7294e08ed55d54b748ddfa1fcc6dcc2dd3e7aa982?color=5a5a5a)

hat für jedes

einen negativen Wert, da

sein muss.
Leitest du

zweimal ab unterscheidet sich diese Ableitung nicht von deren Ursprungsfunktion:
![\(\begin{array}[t]{rll}
f(x) &=& e^{x+1} \\[5pt]
f](https://mathjax.schullv.de/94fc05553d9bef036fabe7fe51f642b92ff5fdf8c5cabba42f18039c512e13c8?color=5a5a5a)
Da diese Funktion keine negativen Funktionswerte enthält, kann sie nie gleiche Funktionswerte der zweiten Ableitung einer nach unten geöffneten Parabel haben.
Aufgabe P3
a)
 Gültigkeit der Gleichung zur Beschreibung von
Gültigkeit der Gleichung zur Beschreibung von  für jeden Wert von
für jeden Wert von  nachweisen
nachweisen
Eine Tangente ist eine Gerade und kann immer durch eine Steigung des Graphen

und einen

-Achsenabschnitt beschrieben werden. Um zu zeigen, dass die in der Aufgabenstellung gegebene Tangente der Tangente an der Stelle

entspricht, musst du nachweisen, dass die Steigung der gegebenen Tangente der Steigung an der Stelle

entspricht und, dass eine Gerade durch den Punkt

mit dieser Steigung den

-Achsenabschnitt

hat.
1.Schritt: Steigung bestimmen
Um die Steigung an der Stelle

zu bestimmen, leitest du die Funktion zunächst ab. Danach setzt du

ein.
![\(\begin{array}[t]{rll}
f_a(x) &=& a \cdot e^{a+x} &\quad \scriptsize \; \\[5pt]
f_a](https://mathjax.schullv.de/fcdb0ba855643a8b525c7d7fbb644e2cb8e1971489e97c7378aae311161a14ba?color=5a5a5a)
Die Steigung entspricht der Steigung der gegebenen Tangente.
2. Schritt:  -Achsenabschnitt überprüfen
-Achsenabschnitt überprüfen
Um zu überprüfen, ob der in der Aufgabenstellung gegebene

-Achsenabschnitt richtig ist, setzt du die Koordinaten des Punkts

in die gegebene Tangentengleichung ein. Entspricht dies einer wahren Aussage, ist der

-Achsenabschnitt korrekt gewählt.
Der in der Aufgabenstellung gegebene

-Achsenabschnitt ist richtig. Damit wird die Tangente am Punkt

durch die Gleichung

beschrieben.
b)
 Flächeninhalt des Dreiecks in Abhängigkeit von
Flächeninhalt des Dreiecks in Abhängigkeit von  berechnen
berechnen
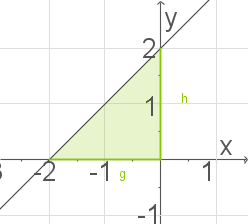 Abb. 1: Dreieck mit
Abb. 1: Dreieck mit 
Um den Flächeninhalt des beschriebenen Dreiecks zu berechnen, benötigst du die Länge

der Grundseite und die Höhe

des Dreiecks. Die Länge der Grundseite entspricht dem Abstand der Nullstelle zum Ursprung.
Die Höhe entspricht dem in der Tangentengleichung gegebenen

-Achsenabschnitt

. Zur Bestimmung der Länge

der Grundseite bestimmst du zunächst die Nullstelle der Tangente:
Die Nullstelle der Tangente ist unabhänig von

immer bei

. Damit ist die Länge der Grundseite des Dreiecks gleich 2.
Der Flächeninhalt des Dreiecks ist somit:
![\(\begin{array}[t]{rll}
A &=& \dfrac{g \cdot h}{2} &\quad \scriptsize \\[5pt]
A &=& \dfrac{2 \cdot 2 \cdot a \cdot e^{a-1}}{2} &\quad \scriptsize \\[5pt]
A &=& 2 \cdot a \cdot e^{a-1} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d84c7a49e8ddf69e603c74c381d4f63abf11bee56dc0159a1a94ac6eacf51bfb?color=5a5a5a)
Der Flächeninhalt des Dreiecks beträgt

.
Aufgabe P4
a)
 Wahrscheinlichkeit für mindestens acht Treffer berechnen
Wahrscheinlichkeit für mindestens acht Treffer berechnen
Du sollst in diesem Aufgabenteil anhand der Abbildung die Wahrscheinlichkeit dafür bestimmen, dass der Basketballer mindestens

-mal trifft, d.h.

ist gesucht. Mit

bezeichnet man die Anzahl der Treffer. Dafür addierst du einfach die Wahrscheinlichkeiten dafür, dass der Basketballer

,

oder

Treffer landet. Die Wahrscheinlichkeiten dafür kannst du in der Abbildung ablesen.
Die Wahrscheinlichkeit, dass der Basketballer mindestens

-mal trifft, liegt also bei ca.

.
b)
 Wahrscheinlickkeit nachweisen
Wahrscheinlickkeit nachweisen
Um zu zeigen, dass die Wahrscheinlichkeit, dass kein Treffer erzielt wird, unter

liegt, musst du die Formel für die
Binomialverteilung verwenden, da die Trefferwahrscheinlichkeit als binominalverteilt angenommen wird.

=

Dabei ist

die Anzahl der Versuche,

die Wahrscheinlichkeit in einem einzelnen Versuch einen Erfolg zu erzielen und

die Anzahl der Erfolge.
Setze also

, um die Wahrscheinlichkeit für keinen Treffer zu berechnen.
Folglich liegt die Wahrscheinlichkeit keinen Treffer zu erzielen unter

Aufgabe P5
a)
 Koordinatenachsen zeichnen
Koordinatenachsen zeichnen
Der Punkt

hat die Koordinaten

, d.h. der
Ursprung des Koordinatensystems liegt in

. Da der Punkt

als erste Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die

-Achse die Gerade

. Die Richtung der

-Achse ist dabei die Richtung des Vektors

. Das Vorgehen bei der

-Achse ist analog. Da der Punkt

als zweite Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die

-Achse die Gerade

. Die Richtung der

-Achse ist dabei die Richtung des Vektors

. Der Punkt

hat als letzte Koordinate eine negative Zahl (die restlichen Koordinaten sind gleich Null), das bedeutet, dass die

-Achse die Gerade

ist. Die Richtung ist dieses Mal allerdings die Richtung des Vektors

.
Somit ergibt sich folgendes Koordinatensystem:
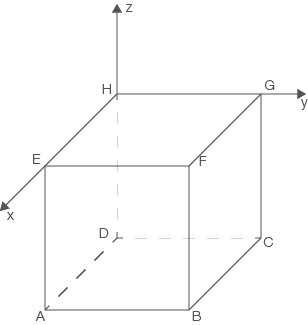 Abb. 2: Würfel im Koordinatensystem
Abb. 2: Würfel im Koordinatensystem
Der Punkt

hat demnach die Koordinaten

b)
 Punkt
Punkt  bestimmen
bestimmen
Sind zwei Punkte

und

gegeben, so ist der
Abstand 
der beiden Punkte definiert als
Der Punkt

soll auf der Kante

des Würfels liegen und soll zum Punkt

(dem Ursprung des Koordinatensystems) den Abstand

haben, d.h.

. Die Koordinaten des zweiten Punkts

sind gegeben. Die Koordinaten des ersten Punkts

kannst du mithilfe des Ortvektors von

und dem Vektor

umschreiben.

mit

Setze nun die Koordinaten der Punkte in die Formel für den Abstand mit

ein und löse die Gleichung nach

auf
Da für

der Punkt

nicht auf der Kante

liegen würde, muss

sein. Für

gilt somit

Somit sind die Koordinaten von

Bildnachweise [nach oben]
© 2016 - SchulLV.
© 2016 - SchulLV.
 an.
an.
 , für den
, für den  gilt.
gilt.
 so gibt, dass der Graph von
so gibt, dass der Graph von  sowohl sprung- als auch knickfrei an den Graphen von
sowohl sprung- als auch knickfrei an den Graphen von  anschließt.
anschließt.
 und dem Graphen von
und dem Graphen von  nie krümmungsruckfrei sein kann.
nie krümmungsruckfrei sein kann.
 die Tangente
die Tangente  durch die Gleichung
durch die Gleichung  beschrieben werden kann.
beschrieben werden kann.
 schließen die Tangente
schließen die Tangente  und die beiden Koordinatenachsen ein Dreieck ein.
Ermittle den Flächeninhalt dieses Dreiecks in Abhängigkeit von
und die beiden Koordinatenachsen ein Dreieck ein.
Ermittle den Flächeninhalt dieses Dreiecks in Abhängigkeit von  .
.
 Freiwürfe. Die Anzahl seiner Treffer wird mit
Freiwürfe. Die Anzahl seiner Treffer wird mit  bezeichnet und durch die Zufallsgröße
bezeichnet und durch die Zufallsgröße  beschrieben.
Die Zufallsgröße
beschrieben.
Die Zufallsgröße  wird als binomialverteilt mit der Trefferwahrscheinlichkeit
wird als binomialverteilt mit der Trefferwahrscheinlichkeit  angenommen.
In der Abbildung ist die Wahrscheinlichkeitsverteilung von
angenommen.
In der Abbildung ist die Wahrscheinlichkeitsverteilung von  dargestellt.
dargestellt.
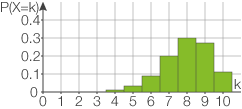 Abb. 1: Wahrscheinlichkeitsverteilung
Abb. 1: Wahrscheinlichkeitsverteilung
 -mal trifft.
-mal trifft.
 ist.
ist.
 . Die Eckpunkte
. Die Eckpunkte  ,
,  ,
,  und
und  dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten:
dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten:  ,
,  ,
,  und
und  .
.
 an.
an.
 liegt auf der Kante
liegt auf der Kante  des Würfels und hat vom Punkt
des Würfels und hat vom Punkt  den Abstand
den Abstand  .
Berechne die Koordinaten des Punktes
.
Berechne die Koordinaten des Punktes  .
.
 Abb. 2: Würfel im Koordinatensystem
Abb. 2: Würfel im Koordinatensystem