Aufgabe 1B
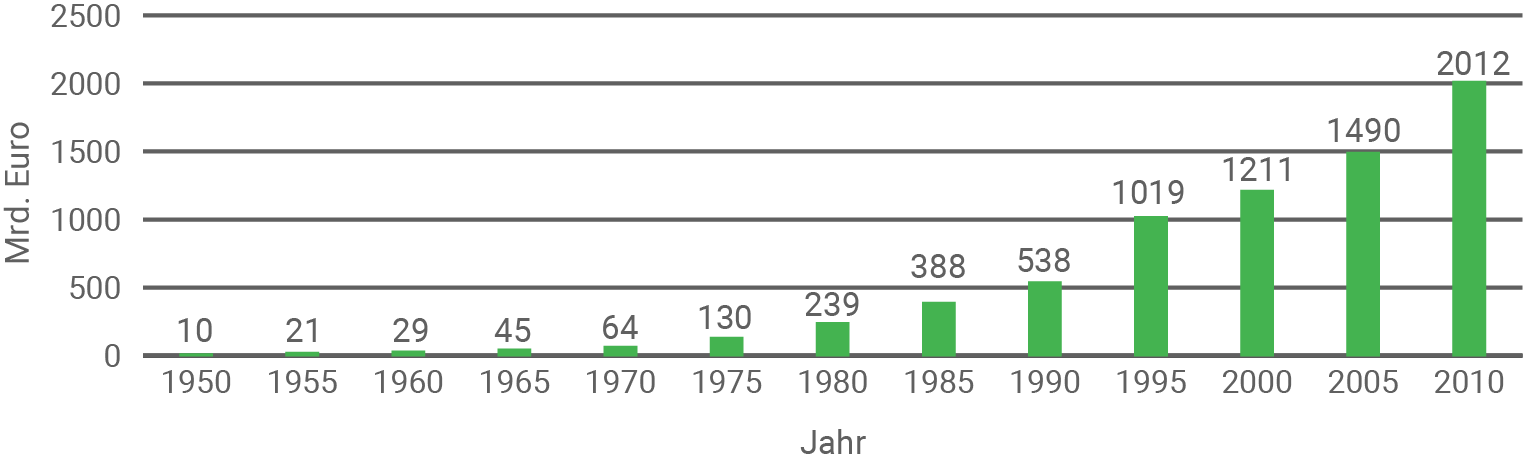
Die Grafik stellt den Schuldenstand Deutschlands in Mrd. Euro jeweils zu Beginn des Jahres ab dem Jahr 1950 dar.
 definierte Funktionenschar
definierte Funktionenschar  mit
mit  , gegeben.
, gegeben.

a)
Gib die beiden Fünfjahreszeiträume an, in denen sich die Schulden mindestens verdoppelt haben.
(2 BE)
b)
Bestimme zwei geeignete Regressionsfunktionen.
Beurteile die von dir gewählten Regressionsfunktionen hinsichtlich ihrer Eignung zur Beschreibung des vorliegenden Sachverhalts.
Beurteile die von dir gewählten Regressionsfunktionen hinsichtlich ihrer Eignung zur Beschreibung des vorliegenden Sachverhalts.
(9 BE)
In einem Modell soll der Anstieg des Schuldenstands gestoppt werden und die Schulden sollen abgebaut werden. Zu Beginn des Jahres 2005 beträgt der Schuldenstand in diesem Modell 1490 Mrd. Euro. Die Änderungsrate des Schuldenstands soll ab Beginn des Jahres 2005 durch die Funktion  mit
mit 
 in Jahren ab dem Jahr 2005,
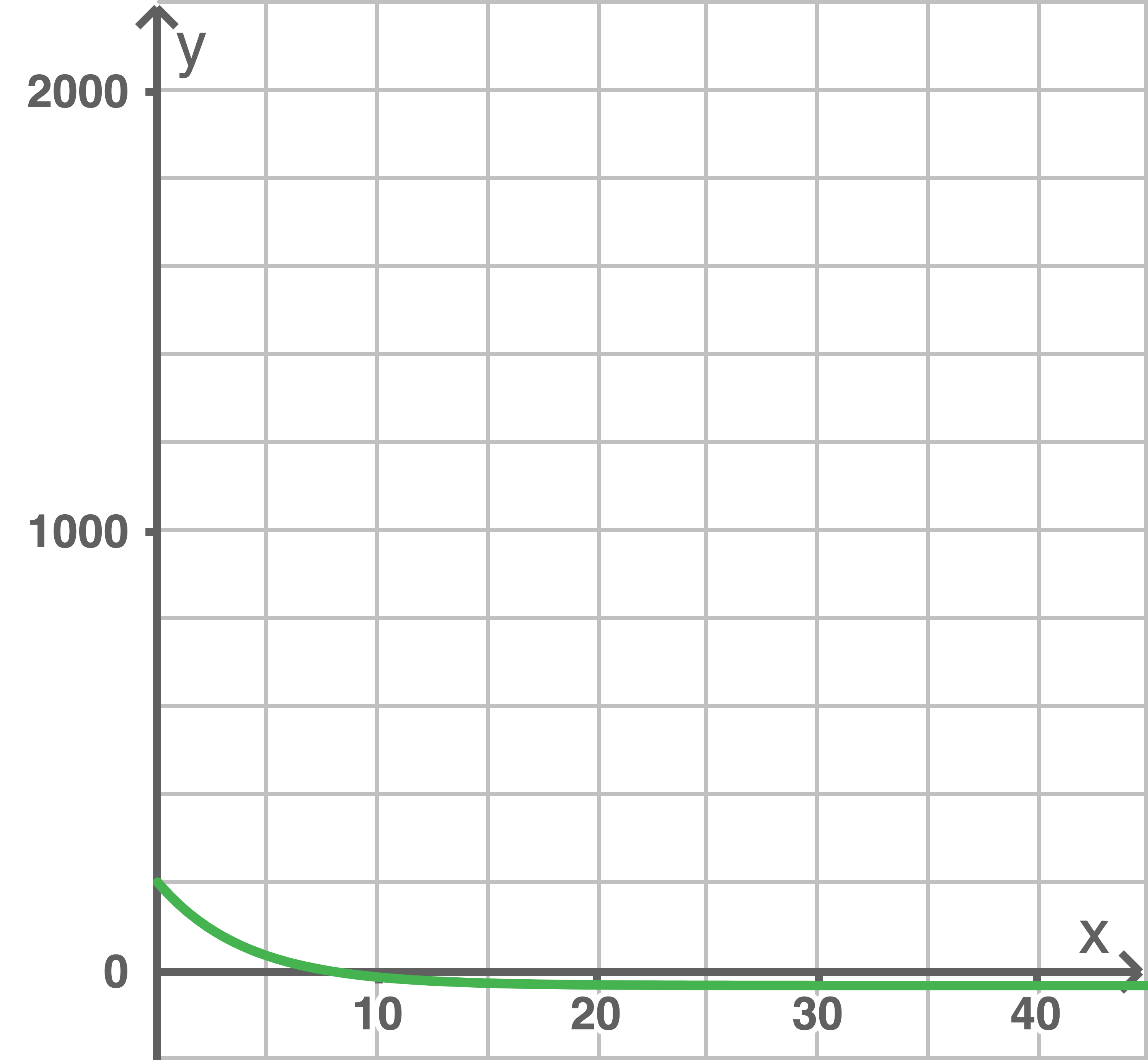
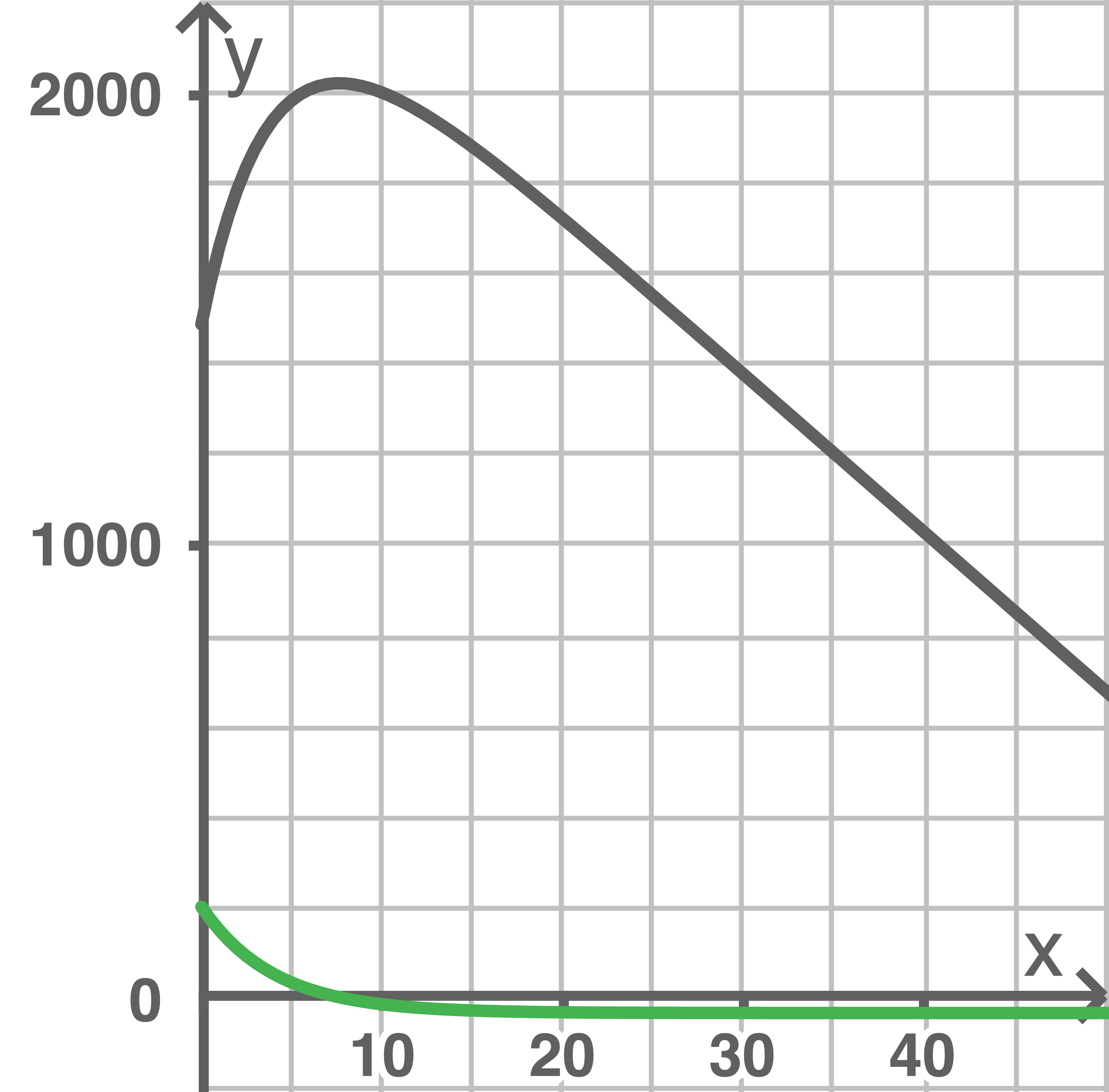
in Jahren ab dem Jahr 2005,  in Mrd. Euro pro Jahr, beschrieben werden. Die Abbildung zeigt den Graphen der Funktion
in Mrd. Euro pro Jahr, beschrieben werden. Die Abbildung zeigt den Graphen der Funktion  .
.

c)
Begründe, dass der nach diesem Modell erwartete Schuldenstand in Mrd. Euro zu Beginn des Jahres 2025 mit dem folgenden Term bestimmt werden kann:

(3 BE)
d)
Skizziere in das Koordinatensystem den nach diesem Modell ungefähr zu erwartenden Schuldenstand vom Beginn des Jahres 2005 bis zum Jahr 2045.
(4 BE)
e)
Berechne für dieses Modell das Jahr, in dem der erwartete Schuldenstand genauso hoch ist wie zu Beginn des Jahres 2005.
(4 BE)
f)
Bestimme den maximalen Schuldenstand sowie das Jahr, in dem dieser erreicht wird.
Unabhängig vom Sachkontext ist die in
(3 BE)
g)
Zeige für  dass der maximale Funktionswert unabhängig vom Wert von
dass der maximale Funktionswert unabhängig vom Wert von  ist.
ist.
(4 BE)
h)
Für jeden Wert von  für
für  wird die Gerade durch den Schnittpunkt mit der
wird die Gerade durch den Schnittpunkt mit der  -Achse und den Hochpunkt des zugehörigen Graphen zu
-Achse und den Hochpunkt des zugehörigen Graphen zu  betrachtet.
betrachtet.
Für alle diese Geraden gilt: Sie schneiden sich in einem Punkt auf der -Achse.
-Achse.
Bestimme die -Koordinate dieses gemeinsamen Punktes auch mithilfe einer Skizze ohne Berechnung der Geradengleichungen.
-Koordinate dieses gemeinsamen Punktes auch mithilfe einer Skizze ohne Berechnung der Geradengleichungen.
Für alle diese Geraden gilt: Sie schneiden sich in einem Punkt auf der
Bestimme die
(6 BE)
i)
Berechne alle Werte von  für die der Graph der Ableitungsfunktion
für die der Graph der Ableitungsfunktion  vollständig unterhalb oder oberhalb des Graphen der Funktion
vollständig unterhalb oder oberhalb des Graphen der Funktion  liegt.
liegt.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
1950 bis 1955 und 1970 bis 1975
b)
Die Regressionsfunktionen können mit dem Taschenrechner bestimmt werden. Hierzu müssen die Wertepaare (Jahr und Schuldenstand) in die Statistik Tabelle eingetragen werden. Nun kann der Taschenrechner mit den eingetragenen Werten verschiedene Regressionsfunktionen aufstellen.
Für den im Schaubild dargestellten Datensatz eignen sich auf den ersten Blick die Exponentielle Regression und die Logistische Regression.
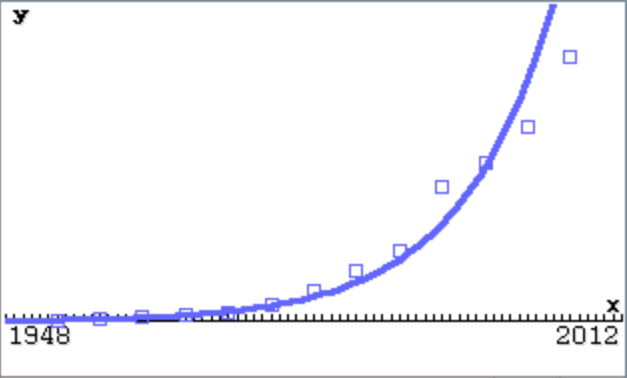 Die Exponentialfunktion eignet sich, um den Schuldenstand in Deutschland zu modellieren, wenn die Regierung sich nicht an die Schuldenbremse hält.
Die Exponentialfunktion eignet sich, um den Schuldenstand in Deutschland zu modellieren, wenn die Regierung sich nicht an die Schuldenbremse hält.
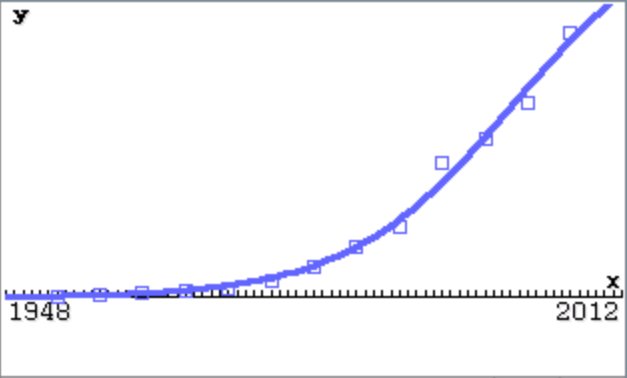 Die logistische Funktion eignet sich, um den Schuldenstand in Deutschland zu modellieren, wenn die Regierung die Schuldenbremse einhält.
Die logistische Funktion eignet sich, um den Schuldenstand in Deutschland zu modellieren, wenn die Regierung die Schuldenbremse einhält.
Exponentielle Regression:
 mit
mit  als Jahreszahl und
als Jahreszahl und  in Mrd. Euro.
in Mrd. Euro.
Logistische Regression
 mit
mit  als Jahreszahl und
als Jahreszahl und  in Mrd. Euro.
in Mrd. Euro.


c)
Die Funktion  gibt die Änderung des Schuldenstands in Mrd. Euro pro Jahr an, daher gibt das Integral von
gibt die Änderung des Schuldenstands in Mrd. Euro pro Jahr an, daher gibt das Integral von  über ein Intervall die Gesamtzunahme der Schulden in dem entsprechenden Zeitraum an. 1490 Mrd. Euro ist der Schuldenstand zu Beginn des Jahres 2005. Die Summe gibt also den Schuldenstand zu Beginn des Jahres 2025 an.
über ein Intervall die Gesamtzunahme der Schulden in dem entsprechenden Zeitraum an. 1490 Mrd. Euro ist der Schuldenstand zu Beginn des Jahres 2005. Die Summe gibt also den Schuldenstand zu Beginn des Jahres 2025 an.
d)
e)
Für  muss gelten:
Mit dem solve-Befehl des CAS ergibt sich
muss gelten:
Mit dem solve-Befehl des CAS ergibt sich  Folglich ist das gesuchte Jahr 2031.
Folglich ist das gesuchte Jahr 2031.
f)
Die Nullstelle der Funktion  kann mit dem CAS bestimmt werden und beträgt
kann mit dem CAS bestimmt werden und beträgt  . Folglich ist der Schuldenstand im Jahr 2012 maximal.
. Folglich ist der Schuldenstand im Jahr 2012 maximal.


 Der maximale Schuldenstand beträgt etwa 2023 Mrd. Euro.
Der maximale Schuldenstand beträgt etwa 2023 Mrd. Euro.
g)
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
h_{a}^{\prime}(x) &=& 0 \\[5pt]
a \cdot (1-2 \cdot a \cdot x) \cdot \mathrm{e}^{2 \cdot a \cdot x} &=& 0 &\quad \scriptsize \mid\; :a \\[5pt]
(1-2 \cdot a \cdot x) \cdot \mathrm{e}^{2 \cdot a \cdot x} &=& 0 &\quad \scriptsize \mid\; :\mathrm{e}^{2 \cdot a \cdot x} \\[5pt]
1-2 \cdot a \cdot x &=& 0 &\quad \scriptsize \mid\; +2ax \\[5pt]
1 &=& 2ax &\quad \scriptsize \mid\; :2a \\[5pt]
\dfrac{1}{2a} &=& x \\[5pt]
x &=& \dfrac{1}{2a} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/3152d6b9069e127a3d49ddb3ca73ed36a8d9b43da80bb58fba13814178496468?color=5a5a5a) Hinreichende Bedingung für Extremstellen:
Hinreichende Bedingung für Extremstellen:
 und
und  . Folglich handelt es sich um einen Hochpunkt.
. Folglich handelt es sich um einen Hochpunkt.
 Somit ist der maximale Funktionswert unabhängig vom Wert von
Somit ist der maximale Funktionswert unabhängig vom Wert von  .
.
h)
Nach Teilaufgabe g) hat der Hochpunkt folgende Koordinaten:  Schnittpunkt mit der
Schnittpunkt mit der  -Achse
-Achse
![\(\begin{array}[t]{rll}
h_{a}(x) &=& 0 \\[5pt]
(1-a \cdot x) \cdot \mathrm{e}^{2 \cdot a \cdot x} &=& 0 &\quad \scriptsize \mid\; :\mathrm{e}^{2 \cdot a \cdot x} \\[5pt]
1-a \cdot x &=& 0 &\quad \scriptsize \mid\; +ax \\[5pt]
1 &=& a \cdot x&\quad \scriptsize \mid\; :a \\[5pt]
\dfrac{1}{a} &=& x \\[5pt]
x &=& \dfrac{1}{a}
\end{array}\)](https://mathjax.schullv.de/0dd20130e3d526ed2f37e8f246134ff41cd1eb2cd2eb23f0112968649a17b334?color=5a5a5a) Somit hat der Schnittpunkt mit der
Somit hat der Schnittpunkt mit der  -Achse folgende Kooridnaten:
-Achse folgende Kooridnaten:  Bestimmung der
Bestimmung der  -Koordinate des Schnittpunkts
-Koordinate des Schnittpunkts
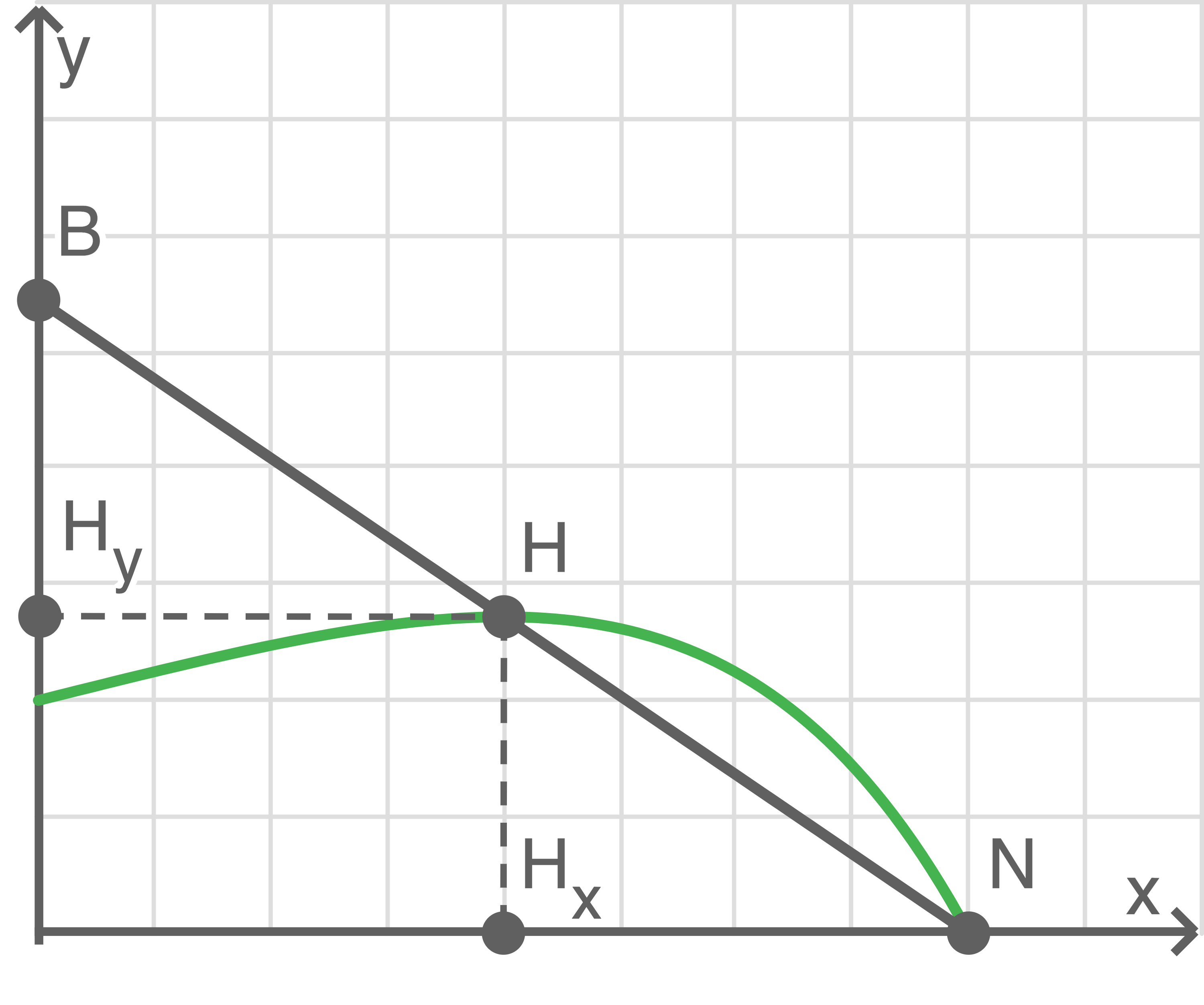
 bezeichnet im Folgenden den Ursprung des Koordinatensystems. Die Strecke
bezeichnet im Folgenden den Ursprung des Koordinatensystems. Die Strecke  ist doppelt so lang wie die Strecke
ist doppelt so lang wie die Strecke  Daher ist auch die Strecke
Daher ist auch die Strecke  doppelt so lang wie die Strecke
doppelt so lang wie die Strecke  . Also hat der gemeinsame Punkt
. Also hat der gemeinsame Punkt  mit der
mit der  -Achse die
-Achse die  -Koordinate
-Koordinate  .
.

i)
Ein Graph liegt vollständig unterhalb oder oberhalb eines anderen Graphen, wenn beide Graphen keine Schnittpunkte haben.
Die Gleichung hat für  und für
und für  keine Lösung, da ansonsten eine Null in einem Nenner stehen würde. Somit existieren für die beiden Werte für
keine Lösung, da ansonsten eine Null in einem Nenner stehen würde. Somit existieren für die beiden Werte für  keine Schnittpunkte zwischen den Graphen zu
keine Schnittpunkte zwischen den Graphen zu  und
und 