Aufgabe 1C
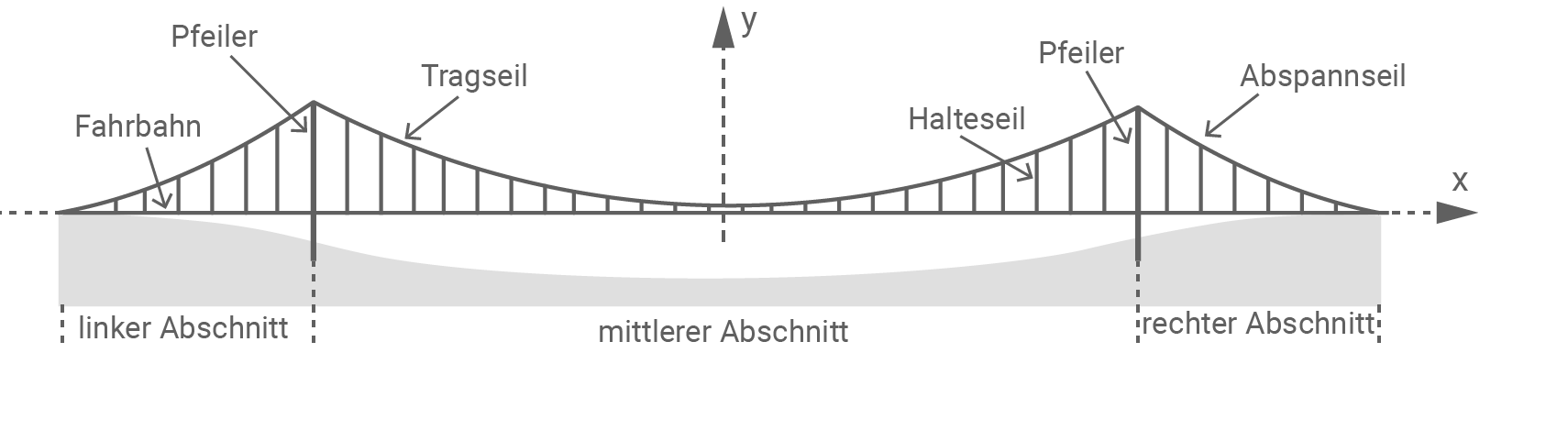
Die Abbildung zeigt schematisch die achsensymmetrische Seitenansicht einer Brücke.
Die beiden vertikalen Pfeiler haben einen Abstand von 
Am oberen Ende jedes Pfeilers ist sowohl das Tragseil des mittleren Abschnitts als auch das Abspannseil des linken bzw. rechten Abschnitts befestigt. Die beiden Abspannseile sind am jeweiligen Ende der Fahrbahn auf Fahrbahnhöhe verankert.
Im Koordinatensystem entspricht eine Längeneinheit 
in der Realität. In der Seitenansicht der Brücke verläuft die 
-Achse entlang der horizontal verlaufenden Fahrbahn, die 
-Achse entlang der Symmetrieachse.
Im rechten Abschnitt der Brücke wird der Verlauf des Abspannseils durch die Funktion 
mit 
beschrieben.
Der Verlauf des Tragseils wird durch die Funktion 
mit 
beschrieben.
a)
Zeige, dass die Fahrbahn der Brücke insgesamt 
lang ist.
(4 BE)
b)
Auch im linken Abschnitt der Brücke kann der Verlauf des Abspannseils durch einen Funktionsterm beschrieben werden.
Gib einen passenden Term 
sowie das Intervall an, in dem dieser Term das Abspannseil darstellt.
(3 BE)
c)
Berechne die Länge eines Pfeilers oberhalb der Fahrbahn.
(3 BE)
d)
Berechne die Größe des Winkels, unter dem das rechte Abspannseil auf den rechten Pfeiler trifft.
(4 BE)
e)
In der Seitenansicht begrenzen der rechte Pfeiler, das Abspannseil und die Fahrbahn ein Flächenstück.
Für eine Baumaßnahme wird zwischen Abspannseil und Fahrbahn eine Teilfläche des Flächenstücks mit einem Schutznetz verkleidet. Links wird die Teilfläche vom Pfeiler begrenzt und rechts endet sie mit einer vertikalen Begrenzung. Die Teilfläche soll halb so groß sein wie das gesamte Flächenstück.
Bestimme den Abstand der vertikalen Begrenzung zum Pfeiler.
Im Folgenden wird der mittlere Abschnitt der Brücke betrachtet. Die 24 vertikal verlaufenden Halteseile verbinden die Fahrbahn mit dem Tragseil. Sie haben von den Pfeilern und untereinander einen horizontalen Abstand von jeweils
(6 BE)
f)
Begründe die Gültigkeit der folgenden Aussage:
Im Term von ist erkennbar, dass die Seitenansicht der Brücke achsensymmetrisch ist.
(2 BE)
g)
Gib die Bedeutung des Terms im Sachzusammenhang an:
Begründe deine Angabe.
(5 BE)
h)
Punkt 
ist der Punkt auf dem rechten Pfeiler, der auf der Höhe der Fahrbahn liegt.
Berechne den Abstand von zum Tragseil.
(7 BE)
i)
Die Punkte 
und 
werden in dieser Reihenfolge durch Strecken verbunden.
Berechne die Summe der Streckenlängen und begründe, dass die Länge des Tragseils größer ist als die Summe der Streckenlängen in der Realität.
(6 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Die Stelle, an der der Graph der Funktion die -Achse schneidet, entspricht im Modell der Stelle, an der das rechte Abspannseil endet.
![\(\begin{array}[t]{rll}
r(x)&=&0 \\[5pt]
2,53 \cdot\left( \mathrm e ^{\frac{1}{11}(32-x)}-1\right)&=& 0
\end{array}\)](https://mathjax.schullv.de/6306c587f0dc676c9dd1adab7f852f8a3649d3aa1f41d163de2357d3e6796ed4?color=5a5a5a)
Mit dem solve-Befehl des CAS ergibt sich 
Aufgrund der Symmetrie der Brücke, ergibt sich die Länge der Fahrbahn zu 
b)
Aufgrund der durch die Symmetrieachse verlaufenden -Achse folgt:
![\(\begin{array}[t]{rll}
l(x)&=& r(-x) \\[5pt]
&=&\dfrac{253}{100} \cdot\left( \mathrm e ^{\frac{1}{11} \cdot(32+x)}-1\right)
\end{array}\)](https://mathjax.schullv.de/e7c395bf417e2f2fbbc29434dd1f50e8d8391293c5a00d4bf3262a1c517696f9?color=5a5a5a)
Da der Abstand der beiden vertikalen Pfeiler 
und somit 
entspricht, gilt für das Intervall, in dem 
das Abspannseil darstellt:
c)
Mit 
folgt, dass die Höhe der Pfeiler über der Fahrbahn ungefähr 
beträgt.
d)
Mit der Kettenregel ergibt sich die erste Ableitung von zu:
![\(\begin{array}[t]{rll}
r^{\prime}(x)&=& \dfrac{253}{100} \cdot\left(-\dfrac{1}{11} \cdot \mathrm e ^{\frac{1}{11}(32-x)}\right)& \\[5pt]
&=& -\dfrac{23}{100} \cdot \mathrm e ^{\frac{1}{11}(32-x)}
\end{array}\)](https://mathjax.schullv.de/d136afe3b383b7865551fa6b5b3c8a62e15bbc7bcbde3388dc9cfd7d1e7cc7ad?color=5a5a5a)
Steigung an der Stelle 
bestimmen:
![\(\begin{array}[t]{rll}
r](https://mathjax.schullv.de/4c5c5a1b45e2d5e2c9ec20205f34f3408f36d9860f558232799fc4182686f8dc?color=5a5a5a)
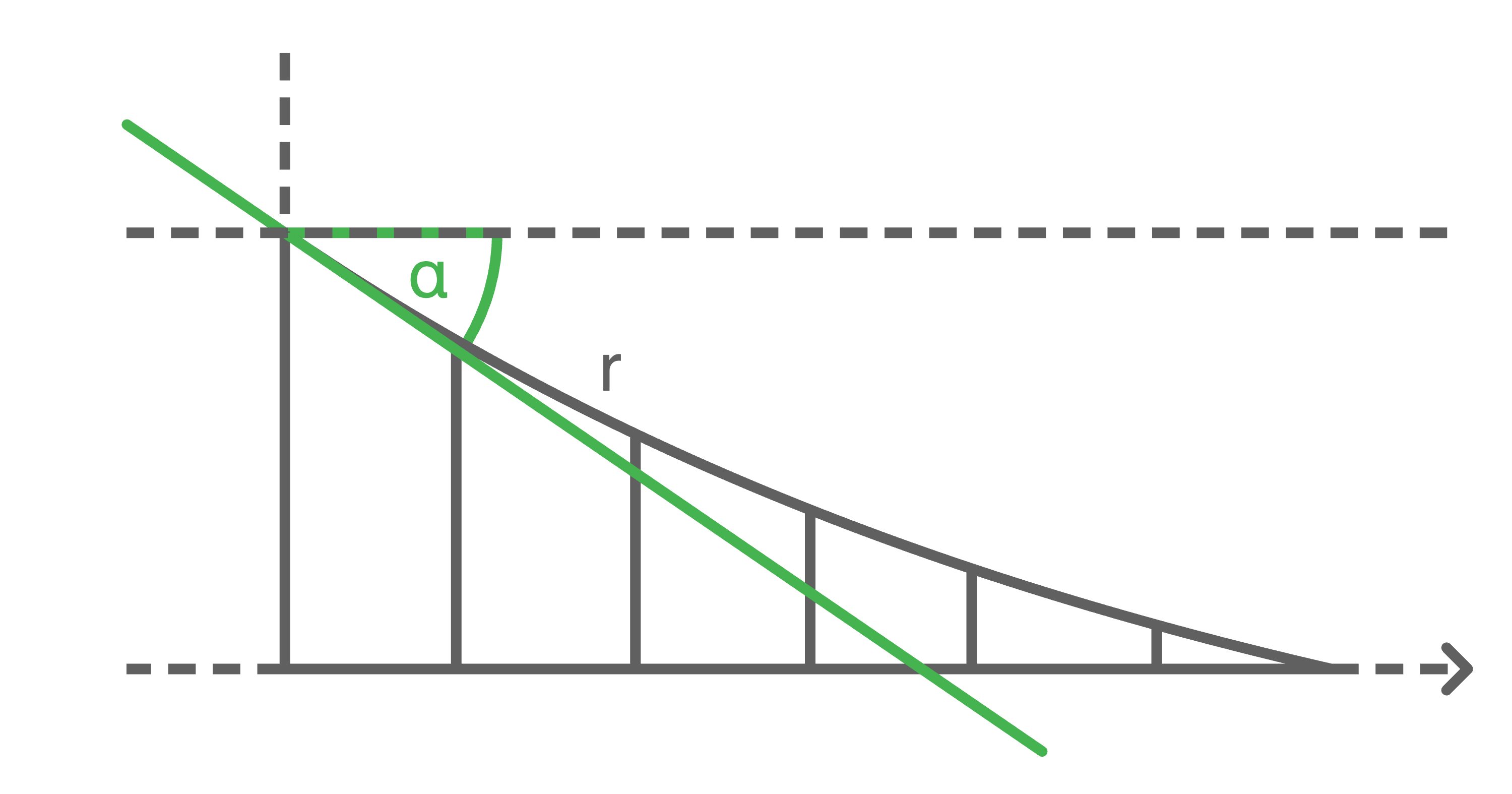
Es gilt nun:
![\(\begin{array}[t]{rll}
\tan (\alpha)&=& r](https://mathjax.schullv.de/9db850084822e616ad4944f650df45f872b03c6323ab380d7cbd69357c0c80d3?color=5a5a5a)
Die gesuchte Winkelgröße ist somit gegeben durch:
![\(\begin{array}[t]{rll}
90^\circ + \alpha &\approx& 90^\circ- 34^\circ & \\[5pt]
&=& 56^\circ
\end{array}\)](https://mathjax.schullv.de/1d6b8ddd4796c961da693bf8f50a3efaf38a88120c1bbe3ec299a2eb9cc8fb8b?color=5a5a5a)
Hilfsskizze
e)
1. Schritt: Inhalt des gesamten Flächenstücks berechnen
Die Fläche wird im Modell durch (Position des Pfeilers) und die Nullstelle bei 
(Ende des Abspannseils) begrenzt.
Daraus folgt mit dem CAS:
![\(\begin{array}[t]{rll}
\displaystyle \int_{20}^{32} r(x) \; \mathrm d x&=& \dfrac{253}{100} \cdot\left(11 \cdot \mathrm e ^{\frac{12}{11}}-23\right)&\\[5pt]
&\approx & 24,66 \; [\,\text{FE}]
\end{array}\)](https://mathjax.schullv.de/d4bcf37b44f5591acafcde1140d47748aef16d49282582f3515b83458cbe7b98?color=5a5a5a)
Der Flächeninhalt des gesamten Flächenstücks beträgt somit etwa 
2. Schritt: Position der vertikalen Begrenzung ermittelm
Für die vertikale Begrenzung an der Stelle 
soll gelten:
![\(\begin{array}[t]{rll}
\displaystyle \int_{20}^{b} r(x) \; \mathrm d x&=& 0,5\cdot \displaystyle \int_{20}^{32} r(x) \; \mathrm d x &\\[5pt]
\displaystyle \int_{20}^{b} r(x) \; \mathrm d x&=& 12,33 \; [\,\text{FE}]
\end{array}\)](https://mathjax.schullv.de/2880d7a902c97d360e93f08373ed366838cae47fce180a1028088bc1b2e60179?color=5a5a5a)
Das CAS liefert 
3. Schritt: Abstand bestimmen
Der Abstand der vertikalen Begrenzung zum Pfeiler ergibt sich nun mit 
und folglich mit 
f)
Die Funktion ist eine ganzrationale Funktion, deren Funktionsterm ausschließlich Potenzen von mit geraden Exponenten enthält.
g)
Bedeutung angeben
Mit dem Term kann die Gesamtlänge der Halteseile im mittleren Brückenabschnitt berechnet werden.
Begründung
Der Term 
gibt mit 
für jedes der 24 Halteseile die jeweilige Länge im Modell an. Der Faktor 10 berücksichtigt den verwendeten Maßstab.
h)
Die Koordinaten von Punkt ergeben sich mit 
Der Punkt auf dem Tragseil, zu dem den minimalen Abstand hat, wird als Punkt 
mit 
bezeichnet.
Da die Strecke 
minimal sein soll, muss diese senkrecht zur Tangente an den Graphen von im Punkt liegen.
Es muss also gelten:
Mit dem CAS folgt 
Der Abstand von zum Tragseil ergibt sich nun mit:
i)
Summe berechnen
Aufgrund der Symmetrie gilt 
Die Summe der Streckenlängen ergibt sich somit durch:
Begründung
Die beiden Strecken 
und 
sind jeweils die kürzesten Verbindungen zwischen zwei Punkten des Graphen von und damit kürzer als das Stück des gekrümmten Graphen von zwischen den jeweiligen Punkten. Deshalb ist die Länge des Tragseils größer als die Summe der Streckenlängen in der Realität.