Aufgabe 2B
Unter den Kunden eines Krankenversicherungsunternehmens haben 
Datenschutzbedenken. Von den Kunden mit Datenschutzbedenken nutzen 
ein Fitnessarmband. 
aller Kunden haben keine Datenschutzbedenken und nutzen ein Fitnessarmband.
Kunden des Unternehmens werden zufällig ausgewählt.
der Fitnessarmbänder falsch eingestellt.
a)
Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.
(3 BE)
b)
Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband. Bestimme die Wahrscheinlichkeit dafür, dass sie Datenschutzbedenken hat.
(3 BE)
c)
Es gilt 
Begründe damit, dass die Ereignisse „Eine unter allen Kunden zufällig ausgewählte Person hat Datenschutzbedenken.“ und „Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband.“ stochastisch abhängig sind.
Begründe damit, dass die Ereignisse „Eine unter allen Kunden zufällig ausgewählte Person hat Datenschutzbedenken.“ und „Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband.“ stochastisch abhängig sind.
(3 BE)
d)
Berechne die Wahrscheinlichkeit dafür, dass mehr als 
der ausgewählten Kunden Datenschutzbedenken haben.
(2 BE)
e)
Setzt man für 
und 
geeignete Werte ein, so kann mit dem Term
die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden.
Gib diese Werte für und an.
Beschreibe das zugehörige Ereignis.
Gib diese Werte für
Beschreibe das zugehörige Ereignis.
(3 BE)
f)
Untersuche, ob es eine natürliche Zahl 
gibt, für die die folgende Aussage richtig ist:
Werden 
Kunden des Unternehmens zufällig ausgewählt, so ist die Wahrscheinlichkeit dafür, dass unter diesen niemand Datenschutzbedenken hat, halb so groß wie bei Kunden.
Bevor Fitnessarmbänder in den Verlauf gelangen, wird ihre Funktionsfähigkeit überprüft. Erfahrungsgemäß sind
(3 BE)
g)
Berechne, wie viele Fitnessarmbänder mindestens überprüft werden müssen, um mit einer Wahrscheinlichkeit von mindestens 
mindestens ein falsch eingestelltes Fitnessarmband zu entdecken.
(3 BE)
h)
An 
Kontrollstationen werden jeweils 
Fitnessarmbänder kontrolliert.
Bestimme die Wahrscheinlichkeit dafür, dass höchstens an einer Kontrollstation mindestens ein falsch eingestelltes Fitnessarmband entdeckt wird.
Bestimme die Wahrscheinlichkeit dafür, dass höchstens an einer Kontrollstation mindestens ein falsch eingestelltes Fitnessarmband entdeckt wird.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
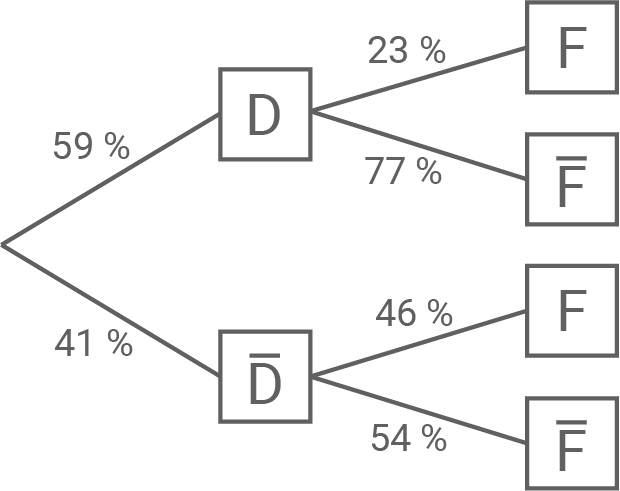
b)
c)
d)
e)
f)
Nach Aufgabenstellung soll gelten:
![\(\begin{array}[t]{rll}
0,41^{2n}&=& 0,5 \cdot 0,41^n \\[5pt]
0,41^n \cdot 0,41^n&=& 0,5 \cdot 0,41^n &\quad \scriptsize \mid\; :0,41^n \\[5pt]
0,41^n&=& 0,5
\end{array}\)](https://mathjax.schullv.de/7fc091cbbad4ff1b2e495b28fb440c5b2f08bd2eb26b39a828184207b6025143?color=5a5a5a)
Da nach Aufgabenstellung eine natrürliche Zahl ist, gilt für jedes , dass 
ist. Folglich gibt es keine natürliche Zahl , für die die Aussage richtig ist.
g)
h)
Die Wahrscheinlichkeit dafür, dass unter 10 Fitnessarmbändern mindestens ein falsch eingestelltes Fitnessarmband beträgt: 
: Anzahl der Kontrollstationen, an denen mindestens ein falsch eingestelltes Fitnessarmband entdeckt wird. ist binomialverteilt mit 
und 
