Aufgabe 1B
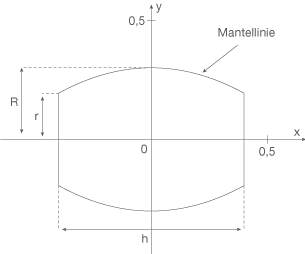
Ein Holzfass ist  hoch, hat in der Mitte einen Radius von
hoch, hat in der Mitte einen Radius von  und an Boden und Deckel den Radius
und an Boden und Deckel den Radius  . Das Fass wird entsprechend der Abbildung im Koordinatensystem symmetrisch zur
. Das Fass wird entsprechend der Abbildung im Koordinatensystem symmetrisch zur  -Achse liegend betrachtet.
-Achse liegend betrachtet.

a) Die Mantellinie kann näherungsweise mithilfe einer Parabel beschrieben werden. Bestimmen Sie für die Mantellinie des Fasses mit den oben genannten Maßen eine Gleichung der Funktion  mit
mit  ,
,  ,
,  .
Berechnen Sie damit das Rotationsvolumen des Fasses.
Johannes Kepler entwickelte die folgende Formel zur Berechnung des Volumens eines Fasses:
.
Berechnen Sie damit das Rotationsvolumen des Fasses.
Johannes Kepler entwickelte die folgende Formel zur Berechnung des Volumens eines Fasses:
 .
Vergleichen Sie Ihr Ergebnis für das Rotationsvolumen des Fasses mit dem Ergebnis, das Sie mithilfe der Keplerschen Fassformel erhalten.
.
Vergleichen Sie Ihr Ergebnis für das Rotationsvolumen des Fasses mit dem Ergebnis, das Sie mithilfe der Keplerschen Fassformel erhalten.

(11P)
Die Mantellinie des Fasses wird in einer anderen Modellierung für  beschrieben durch Funktionsgraphen der Schar
beschrieben durch Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  .
.
b) Begründen Sie, dass die Mantellinie für  beschrieben wird durch die Funktionsgraphen der Schar
beschrieben wird durch die Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  .
Die Graphen der Modellierungsfunktionen der Scharen
.
Die Graphen der Modellierungsfunktionen der Scharen  und
und  sollen die Wölbung des Fasses an der Stelle
sollen die Wölbung des Fasses an der Stelle  jeweils sprung-, knick- und krümmungsruckfrei beschreiben.
Untersuchen Sie, ob es einen Wert für
jeweils sprung-, knick- und krümmungsruckfrei beschreiben.
Untersuchen Sie, ob es einen Wert für  gibt, so dass diese Forderungen erfüllt werden.
gibt, so dass diese Forderungen erfüllt werden.
(12P)
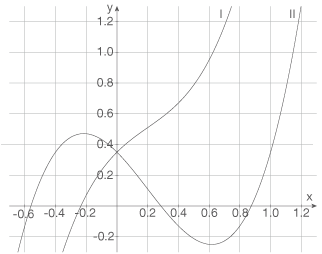
Unabhängig vom Sachzusammenhang werden die Funktionen der Schar  nun für alle
nun für alle  betrachtet. In der Anlage sind beispielhaft zwei Graphen der Schar
betrachtet. In der Anlage sind beispielhaft zwei Graphen der Schar  dargestellt.
Betrachtet werden im Folgenden auch die Tangenten
dargestellt.
Betrachtet werden im Folgenden auch die Tangenten  an die Graphen der Schar
an die Graphen der Schar  an der Stelle
an der Stelle  .
.
c) Entscheiden Sie mithilfe des Verhaltens der Funktionsgraphen an der Stelle  , welcher der Graphen zu einer Funktion mit positivem Parameter
, welcher der Graphen zu einer Funktion mit positivem Parameter  gehört.
Bestimmen Sie eine Gleichung der Tangenten
gehört.
Bestimmen Sie eine Gleichung der Tangenten  an die Graphen der Schar
an die Graphen der Schar  an der Stelle
an der Stelle  .
(Zur Kontrolle:
.
(Zur Kontrolle:  )
Jeder Graph der Schar
)
Jeder Graph der Schar  hat mit der zugehörigen Tangente
hat mit der zugehörigen Tangente  zwei gemeinsame Punkte.
Zeigen Sie, dass deren
zwei gemeinsame Punkte.
Zeigen Sie, dass deren  -Koordinaten jeweils unabhängig vom Parameter
-Koordinaten jeweils unabhängig vom Parameter  sind.
sind.
(13P)
d) Bestimmen Sie die Werte des Parameters  , für die die Minimalstelle
, für die die Minimalstelle
 der Funktionen der Schar
der Funktionen der Schar  existiert.
Entscheiden Sie mithilfe der Lage der Tiefpunkte, für welche Parameterwerte
existiert.
Entscheiden Sie mithilfe der Lage der Tiefpunkte, für welche Parameterwerte  der Graph der zugehörigen Funktion
der Graph der zugehörigen Funktion  mit der
mit der  -Achse als linkem Rand und der
-Achse als linkem Rand und der  -Achse eine Fläche mit endlichem Inhalt einschließt.
-Achse eine Fläche mit endlichem Inhalt einschließt.
(10P)
(46P)
Material
Anlage: Graphen zu Teilaufgabe c)
a)  Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion
Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion  mit
mit  ,
,  ,
,  .
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
.
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
 und
und  Setze
Setze  in
in  ein:
ein:
 Es gilt
Es gilt  . Setze
. Setze  und
und  in
in  ein:
ein:
 Es gilt
Es gilt  . Die Gleichung von
. Die Gleichung von  ist somit gegeben durch
ist somit gegeben durch  .
.
 Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
 Die Grenzen des Integrals sind gegeben durch
Die Grenzen des Integrals sind gegeben durch  und
und  .
.
 Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von
Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von  zeichnen lässt und folgendermaßen vorgehst:
menu
zeichnen lässt und folgendermaßen vorgehst:
menu  4:
4:  3:
3:
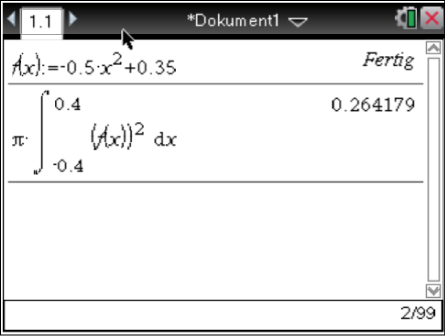 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
.
 Keplersche Fassformel
Die Keplersche Fassformel lautet:
Keplersche Fassformel
Die Keplersche Fassformel lautet:
 .
Du sollst damit das Volumen des Fasses berechnen:
.
Du sollst damit das Volumen des Fasses berechnen:
 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
Die Berechnungen liefern die gleichen Volumina.
.
Die Berechnungen liefern die gleichen Volumina.

b)  Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für
Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für  beschrieben wird durch die Funktionsgraphen der Schar
beschrieben wird durch die Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  . Die Mantellinie ist symmetrisch zur
. Die Mantellinie ist symmetrisch zur  -Achse, also muss
-Achse, also muss  gelten, damit diese Funktionen die Mantellinie beschreiben.
gelten, damit diese Funktionen die Mantellinie beschreiben.
 Die Bedingung ist erfüllt, also wird die Mantellinie für
Die Bedingung ist erfüllt, also wird die Mantellinie für  beschrieben durch die Funktionsgraphen der Schar
beschrieben durch die Funktionsgraphen der Schar  .
.
 Übergang der beiden Funktionen
Damit der Übergang an der Stelle
Übergang der beiden Funktionen
Damit der Übergang an der Stelle  jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
 Überprüfe die Bedingungen:
Überprüfe die Bedingungen:
 erfüllt.
Für
erfüllt.
Für  ist der Übergang sprung-, knick- und krümmungsruckfrei.
ist der Übergang sprung-, knick- und krümmungsruckfrei.
und
- Also muss gelten:
c)  Funktion mit positivem Parameter
Funktion mit positivem Parameter  Der Parameter
Der Parameter  entspricht der Steigung der Tangente an der Stelle
entspricht der Steigung der Tangente an der Stelle  . Die Funktion mit positivem Parameter
. Die Funktion mit positivem Parameter  ist also die Funktion, deren Graph eine positive Steigung an der Stelle
ist also die Funktion, deren Graph eine positive Steigung an der Stelle  hat. Das ist Graph Ⅰ.
hat. Das ist Graph Ⅰ.
 Bestimme die Gleichung der Tangenten
Bestimme die Gleichung der Tangenten  Nutze die Funktion tangentLine deines Taschenrechners, um die Gleichung der Tangente zu berechnen.
menu:
Nutze die Funktion tangentLine deines Taschenrechners, um die Gleichung der Tangente zu berechnen.
menu:  4:
4:  9:
9:
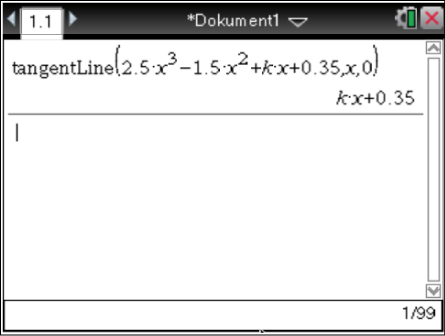 Die Tangentengleichung ist gegeben durch
Die Tangentengleichung ist gegeben durch  .
.
 Schnittstelle der Funktionenschar und der Tangente
Um die
Schnittstelle der Funktionenschar und der Tangente
Um die  -Koordinaten der Schnittpunkte der Funktionenschar mit den Tangenten zu berechnen, musst du diese gleichsetzen:
-Koordinaten der Schnittpunkte der Funktionenschar mit den Tangenten zu berechnen, musst du diese gleichsetzen:
 Nutze deinen Taschenrechner zur Berechnung der Schnittstellen.
Nutze deinen Taschenrechner zur Berechnung der Schnittstellen.
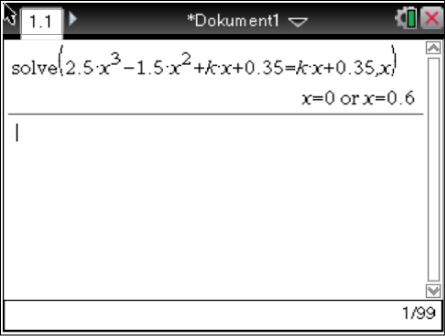 Die gesuchten
Die gesuchten  -Koordinaten sind
-Koordinaten sind  und
und  , beide sind unabhängig von
, beide sind unabhängig von  .
.


d)  Werte des Parameters
Werte des Parameters  bestimmen
Du sollst die Werte für
bestimmen
Du sollst die Werte für  bestimmen, für die die Minimalstelle
bestimmen, für die die Minimalstelle  der Funktionen der Schar
der Funktionen der Schar  existiert.
existiert.
 existiert nur, wenn
existiert nur, wenn  existiert. Es muss also gelten:
existiert. Es muss also gelten:
 Deshalb existiert die Minimalstelle nur für
Deshalb existiert die Minimalstelle nur für  .
.
 Fläche mit endlichem Inhalt
Finde die Parameterwerte für
Fläche mit endlichem Inhalt
Finde die Parameterwerte für  , für welche der Graph der zugehörigen Funktion
, für welche der Graph der zugehörigen Funktion  mit der
mit der  -Achse als linkem Rand und der
-Achse als linkem Rand und der  -Achse eine Fläche mit endlichem Inhalt einschließt. Jeder Graph der Schar
-Achse eine Fläche mit endlichem Inhalt einschließt. Jeder Graph der Schar  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  , dieser liegt oberhalb des Koordinatenursprungs. Damit die Fläche endlich ist, muss der Graph der Funktion die
, dieser liegt oberhalb des Koordinatenursprungs. Damit die Fläche endlich ist, muss der Graph der Funktion die  -Achse schneiden. Der Tiefpunkt des Graphen der Funktionen muss also auf oder unterhalb der
-Achse schneiden. Der Tiefpunkt des Graphen der Funktionen muss also auf oder unterhalb der  -Achse liegen, es muss also gelten:
-Achse liegen, es muss also gelten:
 Definiere dir die Funktion
Definiere dir die Funktion  und nutze die solve-Funktion deines Taschenrechners.
und nutze die solve-Funktion deines Taschenrechners.
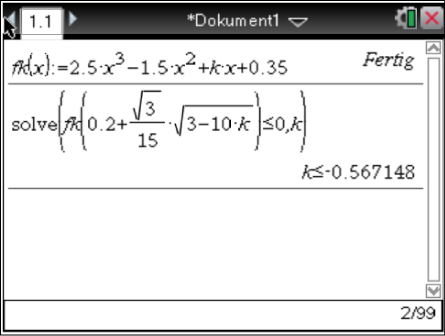 Für die Parameterwerte
Für die Parameterwerte  schließen die Graphen der Schar
schließen die Graphen der Schar  jeweils eine Fläche endlichen Inhalts ein.
jeweils eine Fläche endlichen Inhalts ein.

a)  Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion
Gleichung der Funktion bestimmen
Bestimme für die Mantellinie des Fasses mit den Maßen aus der Aufgabenstellung eine Gleichung der Funktion  mit
mit  ,
,  ,
,  .
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
.
Die Aufgabenstellung liefert dir folgende Punkte, die auf dem Graphen der Funktion liegen:
 und
und  Setze
Setze  in
in  ein:
ein:
 Es gilt
Es gilt  . Setze
. Setze  und
und  in
in  ein:
ein:
 Es gilt
Es gilt  . Die Gleichung von
. Die Gleichung von  ist somit gegeben durch
ist somit gegeben durch  .
.
 Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
Berechne das Rotationsvolumen
Das Rotationsvolumen berechnest du mit folgender Formel:
 Die Grenzen des Integrals sind gegeben durch
Die Grenzen des Integrals sind gegeben durch  und
und  .
.
 Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von
Das Integral kannst du mit dem Taschenrechner berechnen, indem du dir den Graphen von  zeichnen lässt und folgendermaßen vorgehst:
Keyboard
zeichnen lässt und folgendermaßen vorgehst:
Keyboard  2D
2D  CALC
CALC
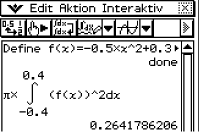 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
.
 Keplersche Fassformel
Die Keplersche Fassformel lautet:
Keplersche Fassformel
Die Keplersche Fassformel lautet:
 .
Du sollst damit das Volumen des Fasses berechnen:
.
Du sollst damit das Volumen des Fasses berechnen:
 Das Volumen des Fasses beträgt
Das Volumen des Fasses beträgt  .
Die Berechnungen liefern die gleichen Volumina.
.
Die Berechnungen liefern die gleichen Volumina.

b)  Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für
Funktionenschar für Mantellinie
Begründe, dass die Mantellinie für  beschrieben wird durch die Funktionsgraphen der Schar
beschrieben wird durch die Funktionsgraphen der Schar  mit
mit  ,
,  ,
,  . Die Mantellinie ist symmetrisch zur
. Die Mantellinie ist symmetrisch zur  -Achse, also muss
-Achse, also muss  gelten, damit diese Funktionen die Mantellinie beschreiben.
gelten, damit diese Funktionen die Mantellinie beschreiben.
 Die Bedingung ist erfüllt, also wird die Mantellinie für
Die Bedingung ist erfüllt, also wird die Mantellinie für  beschrieben durch die Funktionsgraphen der Schar
beschrieben durch die Funktionsgraphen der Schar  .
.
 Übergang der beiden Funktionen
Damit der Übergang an der Stelle
Übergang der beiden Funktionen
Damit der Übergang an der Stelle  jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
jeweils sprung-, knick- und krümmungsruckfrei ist, müssen folgende Bedingungen erfüllt sein:
 Überprüfe die Bedingungen:
Überprüfe die Bedingungen:
 erfüllt.
Für
erfüllt.
Für  ist der Übergang sprung-, knick- und krümmungsruckfrei.
ist der Übergang sprung-, knick- und krümmungsruckfrei.
und
- Also muss gelten:
c)  Funktion mit positivem Parameter
Funktion mit positivem Parameter  Der Parameter
Der Parameter  entspricht der Steigung der Tangente an der Stelle
entspricht der Steigung der Tangente an der Stelle  . Die Funktion mit positivem Parameter
. Die Funktion mit positivem Parameter  ist also die Funktion, deren Graph eine positive Steigung an der Stelle
ist also die Funktion, deren Graph eine positive Steigung an der Stelle  hat. Das ist Graph Ⅰ.
hat. Das ist Graph Ⅰ.
 Bestimme die Gleichung der Tangenten
Bestimme die Gleichung der Tangenten  Nutze die Funktion tanLine deines Taschenrechners, um die Gleichung der Tangente zu berechnen.
Nutze die Funktion tanLine deines Taschenrechners, um die Gleichung der Tangente zu berechnen.
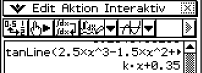 Die Tangentengleichung ist gegeben durch
Die Tangentengleichung ist gegeben durch  .
.
 Schnittstelle der Funktionenschar und der Tangente
Um die
Schnittstelle der Funktionenschar und der Tangente
Um die  -Koordinaten der Schnittpunkte der Funktionenschar mit den Tangenten zu berechnen, musst du diese gleichsetzen:
-Koordinaten der Schnittpunkte der Funktionenschar mit den Tangenten zu berechnen, musst du diese gleichsetzen:
 Nutze deinen Taschenrechner zur Berechnung der Schnittstellen.
Nutze deinen Taschenrechner zur Berechnung der Schnittstellen.
 Die gesuchten
Die gesuchten  -Koordinaten sind
-Koordinaten sind  und
und  , beide sind unabhängig von
, beide sind unabhängig von  .
.


d)  Werte des Parameters
Werte des Parameters  bestimmen
Du sollst die Werte für
bestimmen
Du sollst die Werte für  bestimmen, für die die Minimalstelle
bestimmen, für die die Minimalstelle  der Funktionen der Schar
der Funktionen der Schar  existiert.
existiert.
 existiert nur, wenn
existiert nur, wenn  existiert. Es muss also gelten:
existiert. Es muss also gelten:
 Deshalb existiert die Minimalstelle nur für
Deshalb existiert die Minimalstelle nur für  .
.
 Fläche mit endlichem Inhalt
Finde die Parameterwerte für
Fläche mit endlichem Inhalt
Finde die Parameterwerte für  , für welche der Graph der zugehörigen Funktion
, für welche der Graph der zugehörigen Funktion  mit der
mit der  -Achse als linkem Rand und der
-Achse als linkem Rand und der  -Achse eine Fläche mit endlichem Inhalt einschließt. Jeder Graph der Schar
-Achse eine Fläche mit endlichem Inhalt einschließt. Jeder Graph der Schar  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  , dieser liegt oberhalb des Koordinatenursprungs. Damit die Fläche endlich ist, muss der Graph der Funktion die
, dieser liegt oberhalb des Koordinatenursprungs. Damit die Fläche endlich ist, muss der Graph der Funktion die  -Achse schneiden. Der Tiefpunkt des Graphen der Funktionen muss also auf oder unterhalb der
-Achse schneiden. Der Tiefpunkt des Graphen der Funktionen muss also auf oder unterhalb der  -Achse liegen, es muss also gelten:
-Achse liegen, es muss also gelten:
 Definiere dir die Funktion
Definiere dir die Funktion  und nutze die solve-Funktion deines Taschenrechners.
und nutze die solve-Funktion deines Taschenrechners.
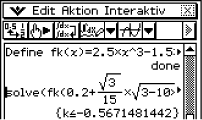 Für die Parameterwerte
Für die Parameterwerte  schließen die Graphen der Schar
schließen die Graphen der Schar  jeweils eine Fläche endlichen Inhalts ein.
jeweils eine Fläche endlichen Inhalts ein.
