Analytische Geometrie
Aufgabe 3A
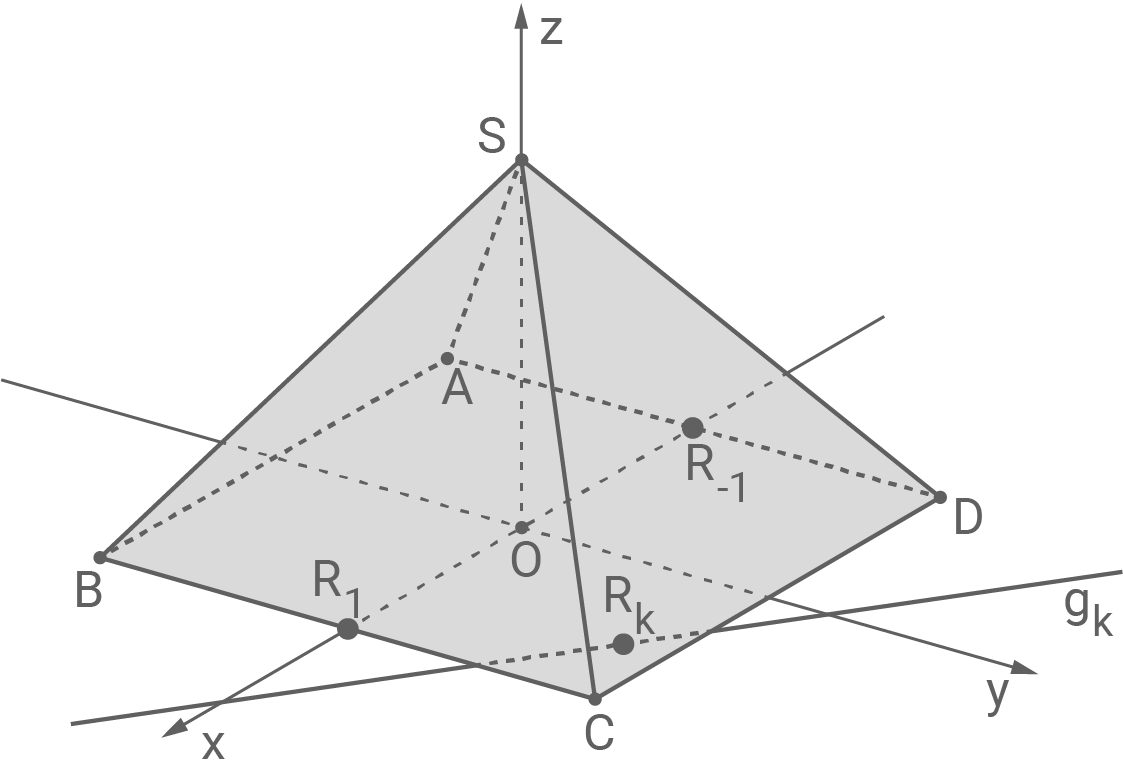
Abbildung 1 zeigt die Pyramide  mit den Eckpunkten
mit den Eckpunkten 


 und
und  sowie den Punkt
sowie den Punkt  der in der quadratischen Grundfläche der Pyramide liegt. Die Seitenfläche
der in der quadratischen Grundfläche der Pyramide liegt. Die Seitenfläche  der Pyramide liegt in der Ebene
der Pyramide liegt in der Ebene 
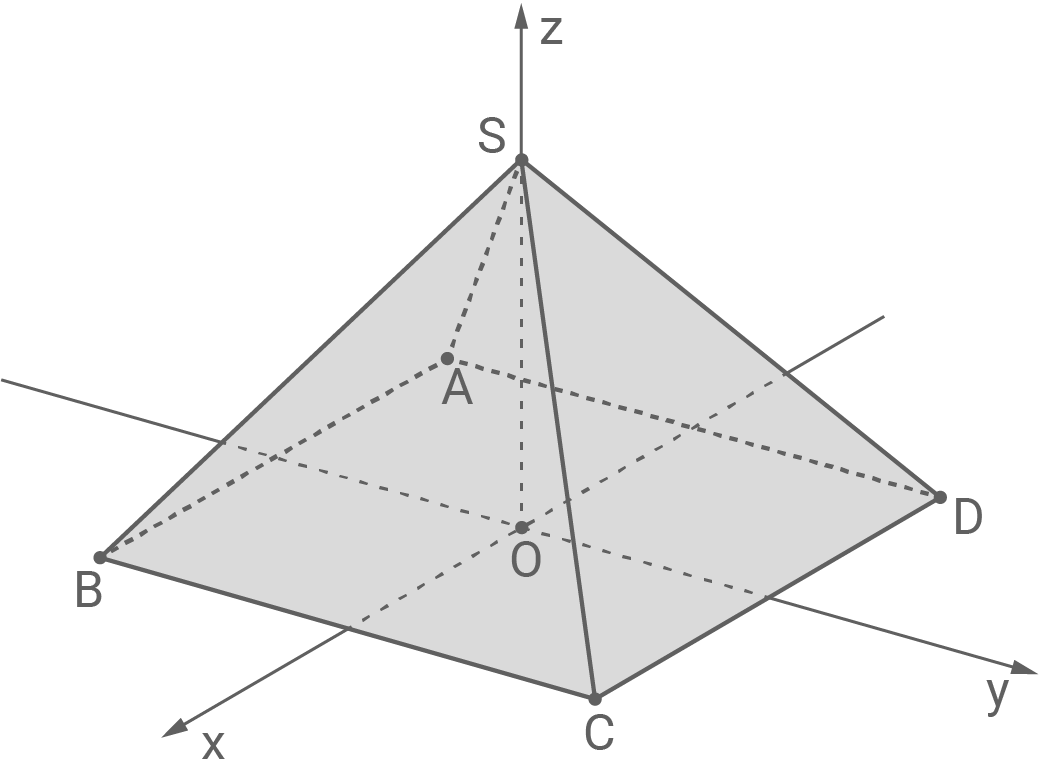

Abbildung 1
a)
Berechne den Inhalt der Oberfläche der Pyramide.
(4 BE)
b)
Bestimme eine Gleichung von  in Koordinatenform.
(zur Kontrolle:
in Koordinatenform.
(zur Kontrolle:  )
)
(3 BE)
c)
Es gibt einen Punkt  der im Innern der Pyramide liegt und von allen vier Seitenflächen sowie der Grundfläche der Pyramide den gleichen Abstand hat. Mithilfe des folgenden Gleichungssystems lässt sich der Wert von
der im Innern der Pyramide liegt und von allen vier Seitenflächen sowie der Grundfläche der Pyramide den gleichen Abstand hat. Mithilfe des folgenden Gleichungssystems lässt sich der Wert von  bestimmen:
bestimmen:
 Gib die geometrische Bedeutung dieser Gleichungen an.
Gib die geometrische Bedeutung dieser Gleichungen an.
Die Ebene
(5 BE)
d)
Zeige, dass der Punkt  in allen Ebenen der Schar enthalten ist.
in allen Ebenen der Schar enthalten ist.
(2 BE)
e)
Weise nach, dass die Größe des Winkels, unter dem die Gerade  die Ebene
die Ebene  schneidet, unabhängig von
schneidet, unabhängig von  ist.
Bestimme die Größe dieses Winkels.
ist.
Bestimme die Größe dieses Winkels.
(5 BE)
Jede Ebene  der Schar schneidet die
der Schar schneidet die  -Ebene in einer Gerade
-Ebene in einer Gerade  Mit
Mit  wird jeweils derjenige Punkt auf
wird jeweils derjenige Punkt auf  bezeichnet, der von
bezeichnet, der von  den kleinsten Abstand hat.
den kleinsten Abstand hat.
In Abbildung 2 sind und
und  beispielhaft für eine Ebene
beispielhaft für eine Ebene  der Schar dargestellt.
der Schar dargestellt.
In Abbildung 2 sind
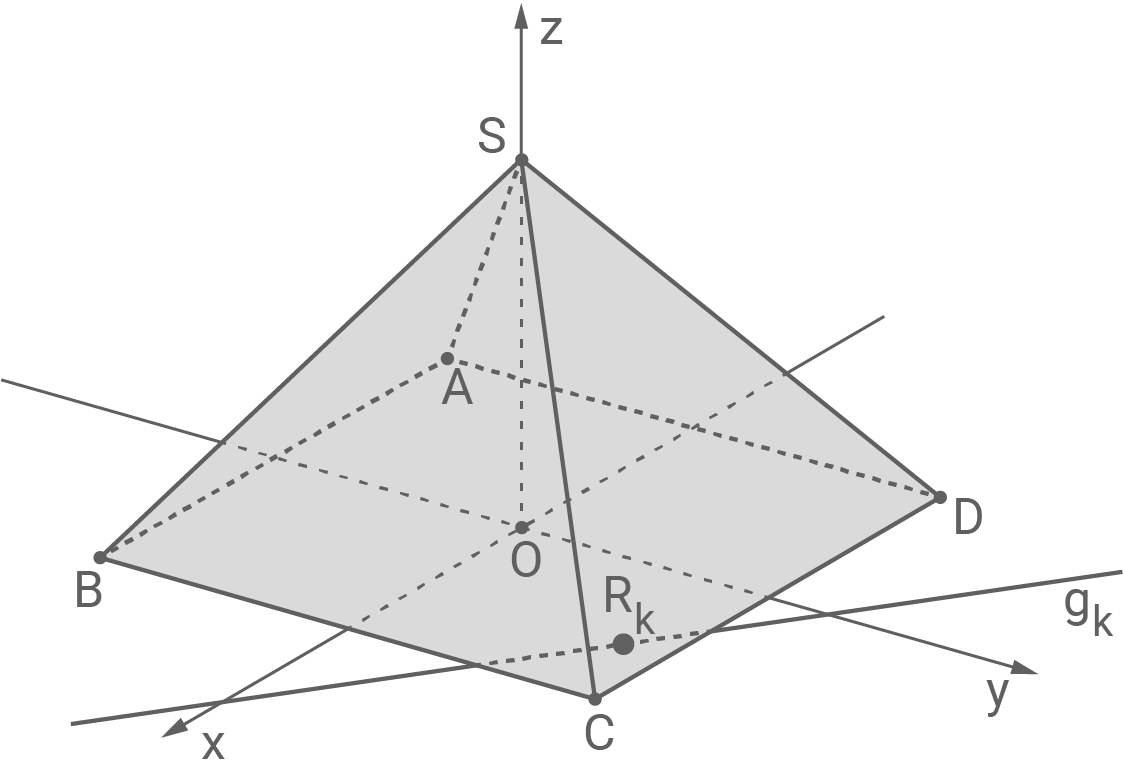
Abbildung 2
f)
Zeichne die Punkte  und
und  in Abbildung 2 ein.
in Abbildung 2 ein.
(3 BE)
g)
Durchläuft  alle Werte von
alle Werte von  bis
bis  dann dreht sich die Fläche
dann dreht sich die Fläche  um die Strecke
um die Strecke  . Dabei entsteht ein Körper.
Beschreibe die Form des entstehenden Körpers und bestimme das Volumen dieses Körpers.
. Dabei entsteht ein Körper.
Beschreibe die Form des entstehenden Körpers und bestimme das Volumen dieses Körpers.
(3 BE)
Aufgabe 3B
Abbildung 1 zeigt modellhaft eine Terrasse, die von zwei Hauswänden und einer Rasenfläche begrenzt wird. Ebenfalls dargestellt ist ein ausfahrbares Sonnendach, im Folgenden als Markise bezeichnet. Der horizontale Boden, zu dem die Terrasse und die Rasenfläche gehören, wird im abgebildeten Koordinatensystem durch die  -Ebene dargestellt. Die Terrasse wird durch das Fünfeck mit den Eckpunkten
-Ebene dargestellt. Die Terrasse wird durch das Fünfeck mit den Eckpunkten 


 und
und  beschrieben. Eine Längeneinheit im Koordinatensystem entspricht dabei 1 m in der Realität.
beschrieben. Eine Längeneinheit im Koordinatensystem entspricht dabei 1 m in der Realität.
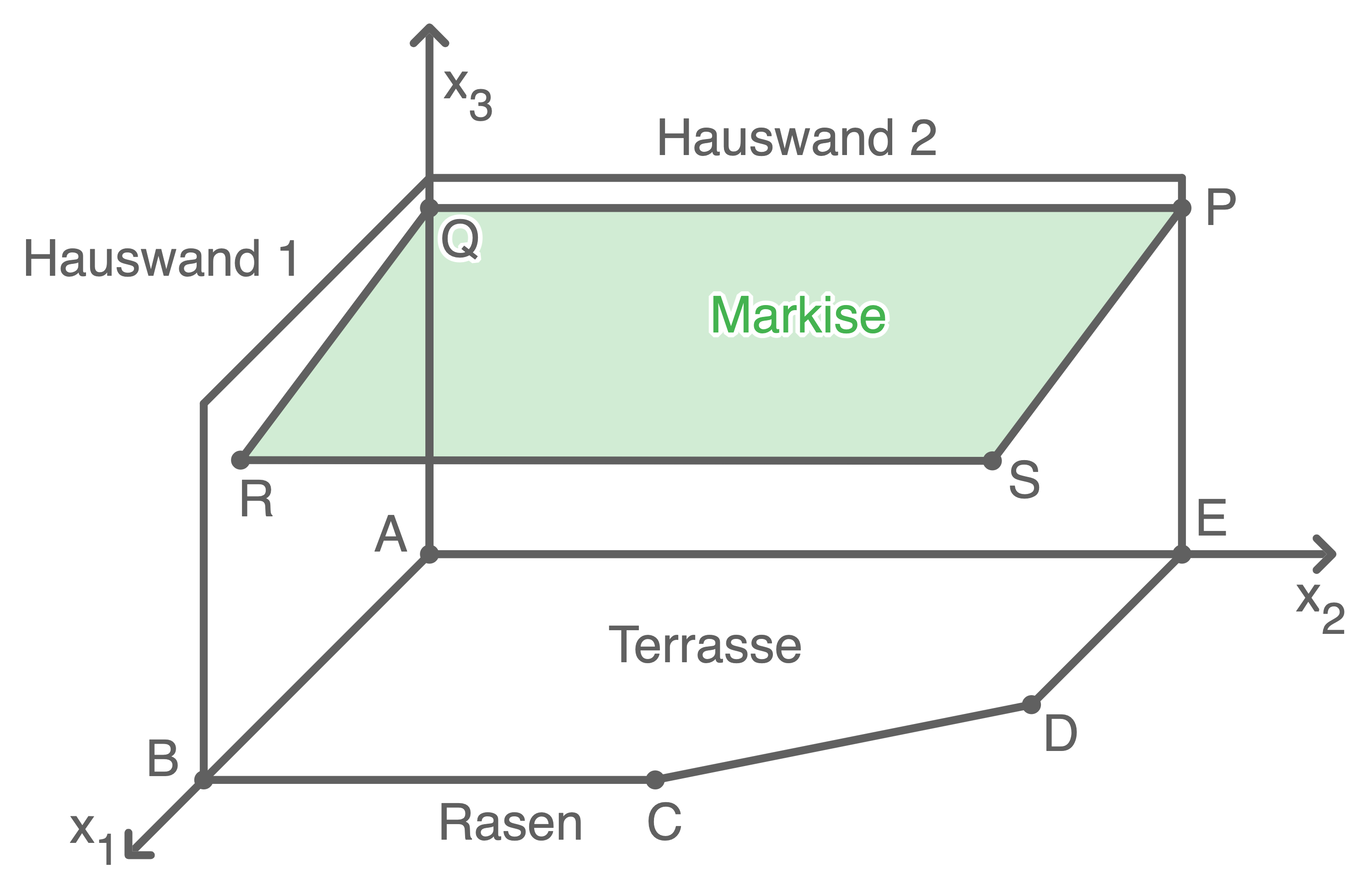
Abbildung 1
a)
Bestimme die Gesamtlänge der an die Terrasse angrenzenden Rasenkanten sowie den Flächeninhalt der Terrasse.
Die Befestigung der Markise an der Hauswand 2 hat die Endpunkte
(6 BE)
b)
Das zu einem bestimmten Zeitpunkt auf die Terrasse einfallende Sonnenlicht wird durch parallele Geraden mit dem Richtungsvektor  beschrieben.
Untersuche, ob zu diesem Zeitpunkt bei vollständig ausgefahrener Markise mehr als die Hälfte der Terrassenfläche im Schatten liegt.
beschrieben.
Untersuche, ob zu diesem Zeitpunkt bei vollständig ausgefahrener Markise mehr als die Hälfte der Terrassenfläche im Schatten liegt.
(7 BE)
Abbildung 2 zeigt die Oberseite der Markise mit ihren beiden gestrichelt dargestellten Gelenkarmen.
Der rechte Gelenkarm besteht aus der oberen Stange  , einem Gelenk im Punkt
, einem Gelenk im Punkt  und einer unteren Stange
und einer unteren Stange  Die obere und die untere Stange sind gleich lang. Beim Ausfahren der Markise verändern sich die Positionen der Punkte
Die obere und die untere Stange sind gleich lang. Beim Ausfahren der Markise verändern sich die Positionen der Punkte  und
und 
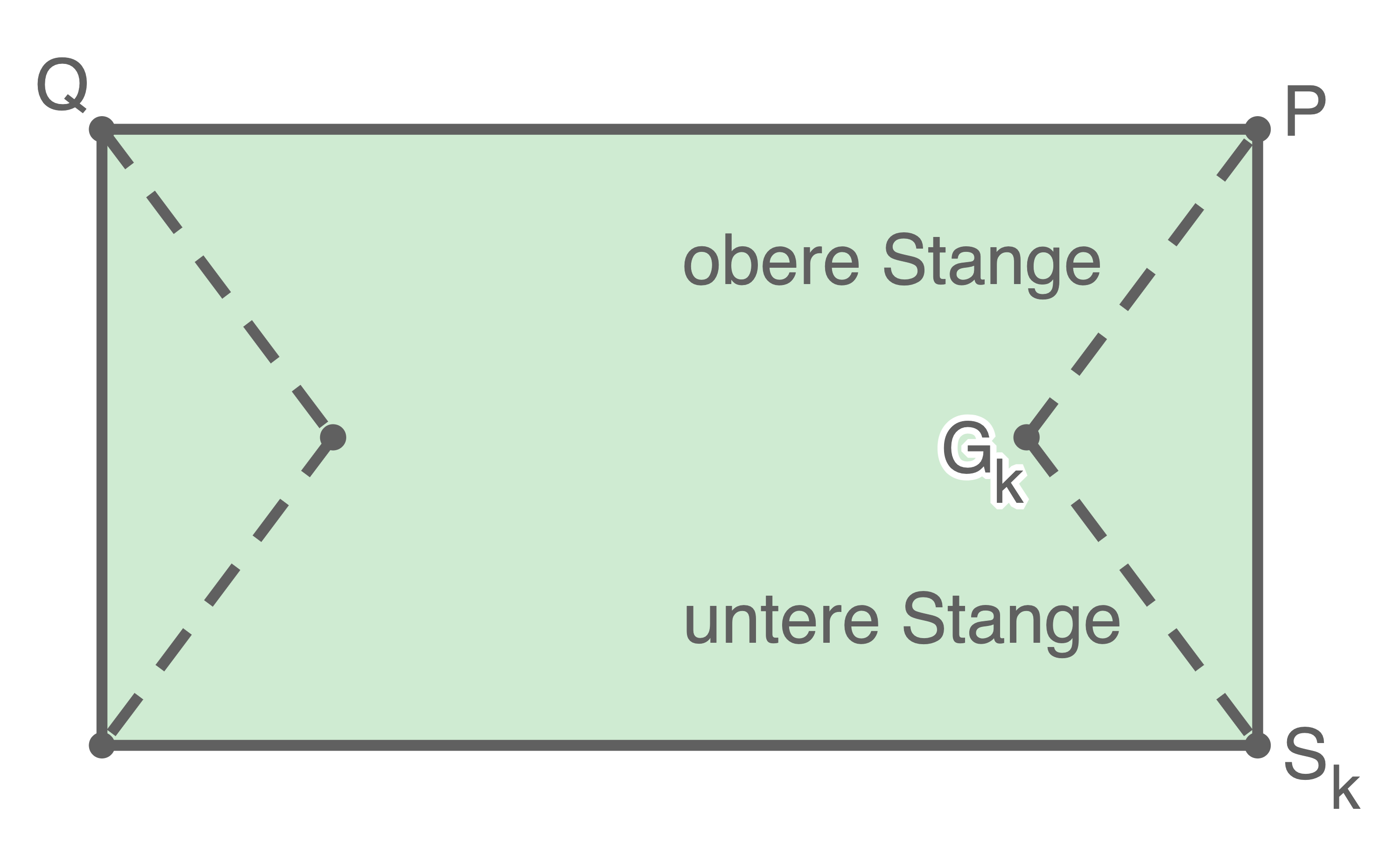
Abbildung 2
c)
Zeige, dass alle Geraden  in der Ebene
in der Ebene  mit
mit  liegen.
liegen.
(4 BE)
d)
Die folgende Rechnung liefert die Größen zweier Winkel:
 liefert
liefert  und damit
und damit  Gib die Bedeutung von
Gib die Bedeutung von  und
und  im Sachzusammenhang an.
im Sachzusammenhang an.
(3 BE)
e)
Sowohl die obere als auch die untere Stange des Gelenkarms sind  lang.
Bestimme die Koordinaten von
lang.
Bestimme die Koordinaten von  für
für  .
.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 3A
a)
Da der Mittelpunkt der Grundfläche der Pyramide durch den Koordinatenursprung gegeben ist und die Koordinaten der vier Eckpunkte  und
und  die Form
die Form  haben folgt, dass die Verbindungsstrecken dieser Punkte jeweils
haben folgt, dass die Verbindungsstrecken dieser Punkte jeweils ![\(6\;[\text{LE}]\)](https://mathjax.schullv.de/b24b80defe1b904fd58e111276594b6358a3e3034b8e4d21a76b43bdfff372b5?color=5a5a5a) lang sind. Für den Ortsvektor des Mittelpunkts
lang sind. Für den Ortsvektor des Mittelpunkts  von der Strecke
von der Strecke  folgt beispielsweise:
folgt beispielsweise:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OB}+\dfrac{1}{2}\cdot\overrightarrow{BC} \\[5pt]
&=&\pmatrix{3\\-3\\0}+\dfrac{1}{2}\cdot\pmatrix{3-3\\3-(-3)\\0-0} \\[5pt]
&=&\pmatrix{3\\0\\0}
\end{array}\)](https://mathjax.schullv.de/b323d73cc79636e939554c0dcfebd71d7407112c4235cc7f16ac790616f1c956?color=5a5a5a) Für die Höhe
Für die Höhe  einer Seitenfläche der Pyramide bezüglich der Kante, die in der
einer Seitenfläche der Pyramide bezüglich der Kante, die in der  -Ebene liegt, folgt somit:
-Ebene liegt, folgt somit:
![\(\begin{array}[t]{rll}
h&=&\left\vert\overrightarrow{MS}\right\vert \\[5pt]
&=&\left\vert\pmatrix{0-3\\0-0\\4-0}\right\vert \\[5pt]
&=&\sqrt{(-3)^2+0^2+4^2} \\[5pt]
&=&5
\end{array}\)](https://mathjax.schullv.de/bb2b6902658b5401465589f71dbbc9be49dde213da1bb6a70677409c6600bc64?color=5a5a5a) Damit beträgt der Flächeninhalt der vier Seitenflächen der Pyramide jeweils
Damit beträgt der Flächeninhalt der vier Seitenflächen der Pyramide jeweils ![\(\dfrac{1}{2}\cdot6\cdot5=15\;[\text{FE}].\)](https://mathjax.schullv.de/5eadbcfc2ea75b57acc7379896dfc9738452b2dd864c5f421b7e4f7b517a33a5?color=5a5a5a) Zusammen mit dem Flächeninhalt von
Zusammen mit dem Flächeninhalt von ![\(6\cdot6=36\;[\text{FE}]\)](https://mathjax.schullv.de/1fa97c4faa38d0dd462233165938651892f6ff3f56ae3575307d20e97065d26c?color=5a5a5a) der quadratischen Grundfläche folgt für den Flächeninhalt
der quadratischen Grundfläche folgt für den Flächeninhalt  der Oberfläche der Pyramide:
der Oberfläche der Pyramide:
![\(O_P=36+4\cdot15=96\;[\text{FE}]\)](https://mathjax.schullv.de/d77e3b60c0d333cc6086ee84141ed790d37a2c73bdb89afe8e1de06aa30fe05d?color=5a5a5a)
b)
c)
Gleichung  besagt, dass der Punkt
besagt, dass der Punkt  auf der Lotgeraden durch
auf der Lotgeraden durch  zu
zu  liegt.
Gleichung
liegt.
Gleichung  liefert, dass der Punkt
liefert, dass der Punkt  zudem in der Ebene
zudem in der Ebene  liegt. Der Abstand des Punktes
liegt. Der Abstand des Punktes  zur Grundfläche der Pyramide, die in der Ebene
zur Grundfläche der Pyramide, die in der Ebene  liegt, beträgt
liegt, beträgt  Die letzte Gleichung sagt somit aus, dass der Abstand, den der Punkt
Die letzte Gleichung sagt somit aus, dass der Abstand, den der Punkt  zur Grundfläche der Pyramide hat, mit dem Abstand von
zur Grundfläche der Pyramide hat, mit dem Abstand von  zu
zu  das heißt aufgrund der Definition von
das heißt aufgrund der Definition von  dem Abstand von
dem Abstand von  zur Ebene
zur Ebene  übereinstimmt.
übereinstimmt.
d)
Einsetzen der Koordinaten von  in die Gleichung der Ebenenschar
in die Gleichung der Ebenenschar  liefert:
liefert:
![\(\begin{array}[t]{rll}
4 k \cdot 0+4 \sqrt{1-k^2} \cdot 0+3 \cdot 4&=&12 \\[5pt]
3\cdot4&=&12 \\[5pt]
12&=&12
\end{array}\)](https://mathjax.schullv.de/949b9a3dae4a4e3a333d07a53ac020768a2796b010145341e5644426692fb90f?color=5a5a5a) Somit ist
Somit ist  in allen Ebenen der Schar enthalten.
in allen Ebenen der Schar enthalten.
e)
Der Schnittwinkel  erfüllt, wenn
erfüllt, wenn  ein Normalenvektor von
ein Normalenvektor von  ist, folgende Gleichung:
ist, folgende Gleichung:
 Für den Ausdruck auf der rechten Seite folgt durch Ablesen eines Normalenvektors von
Für den Ausdruck auf der rechten Seite folgt durch Ablesen eines Normalenvektors von  aus der Ebenengleichung:
Somit hängt
aus der Ebenengleichung:
Somit hängt  und damit auch die Größe des Schnittwinkels
und damit auch die Größe des Schnittwinkels  nicht von
nicht von  ab und für den Winkel gilt:
ab und für den Winkel gilt:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{3}{5} &\quad \scriptsize \mid\; \sin^{-1} \\[5pt]
\alpha&\approx& 36,9^\circ
\end{array}\)](https://mathjax.schullv.de/78977f83ae7614533354ebc6f453b9c410e7d14d99fa2c958781fb36d1b25854?color=5a5a5a)
f)
g)
Der Körper, der durch die Drehung der Fläche  um die Strecke
um die Strecke  entsteht, ist ein Kegel mit Spitze
entsteht, ist ein Kegel mit Spitze  der senkrecht zur in der
der senkrecht zur in der  -Ebene liegenden Grundfläche halbiert wurde.
Die Höhe
-Ebene liegenden Grundfläche halbiert wurde.
Die Höhe  des Kegels ist somit durch die Pyramidenhöhe gegeben, das heißt es gilt
des Kegels ist somit durch die Pyramidenhöhe gegeben, das heißt es gilt  Da die Seiten der Grundfläche der Pyramide
Da die Seiten der Grundfläche der Pyramide  lang sind, folgt für den Flächeninhalt der Grundfläche
lang sind, folgt für den Flächeninhalt der Grundfläche 
![\(G=\pi\cdot\left(\dfrac{6}{2}\right)^2=9\pi\;[\text{FE}]\)](https://mathjax.schullv.de/3e024a7907ea26567b01719664aeb04ae6f45dbe8869277fc16ee2f2985e0da4?color=5a5a5a) Insgesamt folgt damit für das Volumen
Insgesamt folgt damit für das Volumen  des gesuchten Körpers:
des gesuchten Körpers:
![\(V=\dfrac{1}{2}\cdot\left(\dfrac{1}{3}\cdot9\pi \cdot 4\right)=6\pi\;[\text{VE}]\)](https://mathjax.schullv.de/9203a7c2907b0c4f77274f2c83e58dee62802ce173b36d7e576d78c9158e96d1?color=5a5a5a)
Lösung 3B
a)
Gesamtlänge bestimmen
Flächeninhalt berechnen
Die Fläche der Terrasse kann durch ein Rechteck mit den Seiten  und
und  und durch ein Trapez dargestellt werden.
Hierfür gilt:
und durch ein Trapez dargestellt werden.
Hierfür gilt:
![\(\begin{array}[t]{rll}
A_{\text{Rechteck}}&=& \left| \overrightarrow{AB} \right| \cdot \left| \overrightarrow{BC} \right|& \\[5pt]
&=& 3\cdot 3& \\[5pt]
&=& 9 \; [\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/c59fb9f44dcebac87ccabff9f66be23fef999a33cae9afba33d0a9872880c86e?color=5a5a5a) Der vierte Eckpunkt des Quadrates liegt zwischen
Der vierte Eckpunkt des Quadrates liegt zwischen  und
und  und besitzt die Koordinaten
und besitzt die Koordinaten  Für das Trapez folgt also:
Für das Trapez folgt also:
![\(\begin{array}[t]{rll}
A_{\text{Trapez}}&=& \left| \overrightarrow{QE} \right| \cdot \left(\dfrac{ \left| \overrightarrow{CQ} \right|+\left| \overrightarrow{DE} \right|}{2}\right)& \\[5pt]
&=& 2\cdot\dfrac{3+2}{2}& \\[5pt]
&=& 5 \; [\text{m}^2]
\end{array}\)](https://mathjax.schullv.de/25b92587f5627d05e0b35a249fc238be4e1c5b8a8a08cff62d1aef490f373a61?color=5a5a5a) Der gesamte Flächeninhalt ergibt sich also zu:
Der gesamte Flächeninhalt ergibt sich also zu:
![\(\begin{array}[t]{rll}
A&=& A_{\text{Rechteck}} + A_{\text{Trapez}} &\\[5pt]
&=& 9 \; \text{m}^2 + 5 \; \text{m}^2 &\\[5pt]
&=& 14 \; \text{m}^2
\end{array}\)](https://mathjax.schullv.de/2e3163ac1dd9101d220f4a08056cbc977a1087e23aa974b933ac2a88b16ed026?color=5a5a5a)
b)
Anhand des Richtungsvektors der Sonnenstrahlen ergibt sich, dass der Lichteinfall parallel zur Hauswand 1 erfolgt und somit in der Abbildung von vorne auf die Terrasse scheint.
Der Schatten von  liegt also parallel zu Hauswand 2 und ist die Begrenzungslinie des Schattens auf der Terrasse.
Diese Linie wird begrenzt durch die Schattenpunkte von
liegt also parallel zu Hauswand 2 und ist die Begrenzungslinie des Schattens auf der Terrasse.
Diese Linie wird begrenzt durch die Schattenpunkte von  und
und  Für den Schattenpunkt
Für den Schattenpunkt  von
von  muss gelten:
muss gelten:
 Aus der dritten Zeile ergibt sich:
Aus der dritten Zeile ergibt sich:
![\(\begin{array}[t]{rll}
1,9-2r&=& 0 &\quad \scriptsize \mid\; +2r \\[5pt]
1,9&=& 2r &\quad \scriptsize \mid\; :2 \\[5pt]
0,95&=& r
\end{array}\)](https://mathjax.schullv.de/09b10a5f80e8f32869f9363adc95735a6c3b076df587db54bbfa0bdda09fafad?color=5a5a5a) Einsetzen in die Geradengleichung liefert:
Einsetzen in die Geradengleichung liefert:
![\(\begin{array}[t]{rll}
\overrightarrow{OR](https://mathjax.schullv.de/b1e75e062cc4d4f01c4b985e78790b660eb0a68366c184116573e4180d39668b?color=5a5a5a) Aufgrund der Parallelität der Schattenlinie zur Hauswand 2 liegt die Terrasse also bis zu einem Abstand von
Aufgrund der Parallelität der Schattenlinie zur Hauswand 2 liegt die Terrasse also bis zu einem Abstand von  von Hauswand 2 im Schatten.
Da jeder Punkt der Terrasse maximal
von Hauswand 2 im Schatten.
Da jeder Punkt der Terrasse maximal  von der Hauswand 2 entfernt ist, liegt mehr als die Hälfte der Terrasse im Schatten.
von der Hauswand 2 entfernt ist, liegt mehr als die Hälfte der Terrasse im Schatten.
c)
Einsetzen des allgemeinen Geradenpunkts von  in die Ebenengleichung von
in die Ebenengleichung von  liefert:
Somit liegen alle Geraden der Schar in der Ebene
liefert:
Somit liegen alle Geraden der Schar in der Ebene 
d)
Bei vollständig ausgefahrener Markise beschreibt  die Größe des Winkels zwischen der hinteren Kante der Markise und der oberen Stange.
Folglich ist
die Größe des Winkels zwischen der hinteren Kante der Markise und der oberen Stange.
Folglich ist  die Größe des Winkels zwischen den beiden Stangen des Gelenkarms.
die Größe des Winkels zwischen den beiden Stangen des Gelenkarms.
e)
Gleichung von  aufstellen:
aufstellen:
 Für die Länge des Richtungsvektors gilt:
Für die Länge des Richtungsvektors gilt:
 Da die Stange eine Länge von
Da die Stange eine Länge von  besitzt, ergibt sich:
besitzt, ergibt sich:
![\(\begin{array}[t]{rll}
\overrightarrow{OG_{0,5}} &=& \pmatrix{0\\5\\2,3}+ \dfrac{1,28}{1,46} \cdot \pmatrix{1,2\\-0,8\\-0,2} &\\[5pt]
&\approx& \pmatrix{1,05\\4,3\\2,12}
\end{array}\)](https://mathjax.schullv.de/e1bf1f04a7dc86aa26601c6c6e531adcf477896e08be522bac8ed1a99974878f?color=5a5a5a)
 besitzt für
besitzt für  somit die Koordinaten
somit die Koordinaten 