Aufgabe 3B

Das Rechteck $OAEK$ stellt ein Tennisspielfeld dar. Die Koordinaten für die folgenden Punkte lauten:
$O(0\mid 0\mid 0),$ $A(27\mid 0\mid 0),$ $B(27\mid 18\mid 0),$ $C(27\mid 39\mid 0),$ $E(27\mid 78\mid 0),$ $F(27\mid 39\mid 3,5),$ $H(0\mid 39\mid 3,5)$ und $M(13,5\mid 39\mid 3).$
Alle Koordinaten haben die Längeneinheit Fuß $(\text{ft})$ . Das Netz ist an Pfosten befestigt, die durch die Strecken $\overline{CF}$ und $\overline{GH}$ dargestellt sind. Es hat an den Enden eine Höhe von $3,5\,\text{ft}$ und fällt geradlinig ab, bis es in der Mitte $M$ nur noch eine Höhe von $3\,\text{ft}$ hat. Der Boden wird durch die $xy-$ Ebene dargestellt. Der Ball wird als punktförmig angenommen.

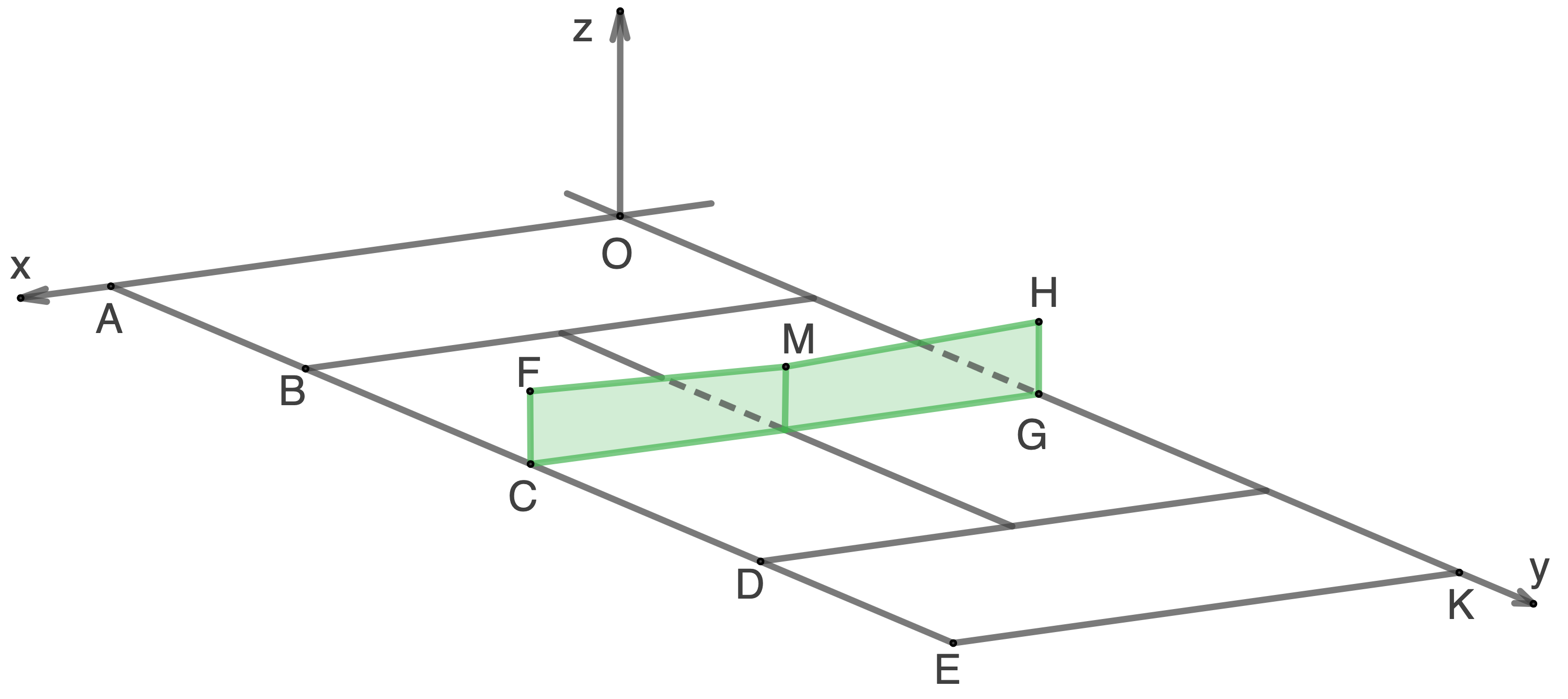
3D-Diagramm eines Koordinatensystems mit Punkten A bis K und einem grünen Rechteck.

Gib die Koordinaten des Punktes $D$ an.
Berechne die Länge der Diagonalen des Spielfeldes.

(3 BE)

Es kann vorausgesetzt werden, dass beim Aufschlag der Ball das Netz überquert und dass die $x-$ Koordinate zu diesem Zeitpunkt größer als 13,5 ist. Die Flugbahn des Balls wird als geradlinig angenommen.
Bei einem Aufschlag wird der Ball im Punkt $P(13\mid 0\mid 10,4)$ getroffen, fliegt in Richtung
$\overrightarrow{v}=\pmatrix{13\\58,5\\-10,4}$ und trifft im Punkt $Q$ auf dem Boden auf.

Zeige, dass $Q$ im Spielfeld liegt.
[zur Kontrolle: $Q(26\mid 58,5\mid 0)$ ]

(4 BE)

Die Geschwindigkeit des Balles wird mit 90 Fuß pro Sekunde als konstant angenommen.
Bestimme, wie viel Zeit vom Abschlag im Punkt $P$ bis zum Auftreffen des Balles auf dem Boden vergeht.

(3 BE)

Berechne die Größe des Winkels, unter dem der Ball auf den Boden auftrifft.

(3 BE)

Spiegelt man die Gerade, die die Flugbahn des Balles beschreibt, an der $xy-$ Ebene, ergibt sich die Gerade $b.$ Die Gerade $b$ beschreibt die Flugbahn direkt nach dem Aufprall.
Bestimme eine Gleichung der Geraden $b.$

(4 BE)

Bei einem anderen Aufschlag wird der Ball im Punkt $P_h(13\mid 0\mid h), h\gt 0,$ abgeschlagen und trifft im Punkt $Q(26\mid 58,5\mid 0)$ auf dem Boden auf. Der Ball überquert das Netz in einer Höhe von $0,2 5\,\text{ft}$ über dem Netz.
Bestimme den zugehörigen Wert von $h.$

(8 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\overrightarrow{OD}= \overrightarrow{OC}+\overrightarrow{BC}= \pmatrix{27\\60\\0}$
Der Punkt $D$ hat die Koordinaten $(27 \mid 60 \mid 0).$

Für die Länge der Diagonalen ist $\mid \overrightarrow{OE}\mid$ gesucht, also $\, \left| \, \pmatrix{27\\78\\0} \,\right| \, = \sqrt{27^2+78^2} \approx 82,5.$
Die Diagonale ist ungefähr $82,5 \,\text{ft}$ lang.

Der Punkt $Q$ liegt auf der Flugbahn des Balles und hat $z-$ Koordinate 0, es gilt also

$\pmatrix{x\\y\\0}=\pmatrix{13\\0\\10,4}+r\cdot \pmatrix{13\\58,5\\-10,4}$

Aus der letzten Zeile lässt sich $r=1$ ablesen. Damit sind die Koordinaten des Punktes $Q$ gegeben durch $Q(26\mid58,5\mid0).$
Das Spielfeld ist in $x-$ Richtung beschränkt durch $0$ und $27$ und in $y-$ Richtung durch $0$ und $78.$

Es gilt $0\lt 26 \lt 27$ und $0 \lt 58,5 \lt 78.$ Damit liegt der Punkt $Q$ im Spielfeld.

Die Länge der Strecke, die der Ball zurücklegt, wird beschrieben durch $\mid \overrightarrow{PQ} \mid.$

$\overrightarrow{PQ}=\pmatrix{26-13\\58,5-0\\0-10,4}=\pmatrix{13\\58,5\\-10,4}$

$\mid\overrightarrow{PQ}\mid=\sqrt{13^2+58,5^2+(-10,4)^2}$ $\approx60,8[\,\text{ft}]$

Die für den Weg benötigte Zeit lässt sich berechnen durch $\dfrac{60,8\,\text{ft}}{90\dfrac{\,\text{ft}}{\,\text{s}}}\approx 0,68\,\text{s}.$

Die Zeit vom Abschlag bis zum Auftreffen des Balles auf dem Boden beträgt ungefähr $0,68\,\text{s}.$

Der Normalenvektor der Grundfläche ist gegeben durch $\overrightarrow{n}=\pmatrix{0\\0\\1}.$

Der Winkel $\alpha$ zwischen der Grundfläche und dem Richtungsvektor $\overrightarrow{v}$ der Fluggeraden des Balles lässt sich wie folgt berechnen:

Vollständigen Rechenweg anzeigen

$\sin(\alpha)\approx0,17 \,\,\,\mid\sin^{-1}$

$\alpha\approx 9,8^{\circ}$

Der Ball trifft ungefähr in einem Winkel von $9,8^{\circ}$ auf dem Boden auf.

Aus der Aufgabenstellung ist bekannt, dass der Ball an dem Punkt $P(13 \mid 0 \mid 10,4)$ getroffen wird und am Punkt $Q(26 \mid 58,5 \mid 0)$ auf dem Boden auftritt.
Wenn der Punkt $P$ an der $xy$ -Ebene gespiegelt wird, ergibt sich der Punkt $\(P$ Die Koordinaten des Punktes $Q$ verändern sich durch die Spiegelung nicht, da dieser auf der $xy$ -Ebene liegt.

$\(\overrightarrow{P$

Die Gerade $b$ verläuft durch die Punkte $Q$ und $\(P$ Die Flugbahn nach dem Aufprall ist damit gegeben durch $\(b: \overrightarrow{x} = \overrightarrow{OQ}+ r \cdot \overrightarrow{P$ $=\pmatrix{26\\58,5\\0}+r \cdot \pmatrix{13\\58,5\\10,4}.$

Die Gleichung der Geraden, die die Flugbahn des Balles beschreibt, ist gegeben durch $k: \overrightarrow{x}=\overrightarrow{OP_h}+s\cdot \overrightarrow{P_hQ}$ $=\pmatrix{13\\0\\h}+s\cdot \pmatrix{26-13\\58,5-0\\0-h}$ $=\pmatrix{13\\0\\h}+s\cdot \pmatrix{13\\58,5\\-h}$

Der Punkt $U,$ in dem der Ball das Netz überquert, hat die $y-$ Koordinate $39.$ Die Koordinaten von $U$ lassen sich also durch folgende Gleichung ermitteln:

$\pmatrix{x\\39\\z_1}=\pmatrix{13\\0\\h}+s\cdot \pmatrix{13\\58,5\\-h}$

Die mittlere Zeile liefert $s=\dfrac{2}{3}.$ Damit ergeben sich für den Punkt $U$ die Koordinaten $(\dfrac{65}{3}\mid 39 \mid \dfrac{h}{3}).$

Die Oberkante des Netzes auf der betrachteten Seite wird beschrieben durch die Gerade

Vollständigen Rechenweg anzeigen

$l: \overrightarrow{x}=\pmatrix{27\\39\\3,5}+t\cdot \pmatrix{-13,5\\0\\-0,5}$

Nun muss noch die Höhe des Punktes auf dem Netz berechnet werden, an dem der Ball dieses überquert, wobei $x=\dfrac{65}{3}$ und $y=39$ aus obigen Überlegungen schon bekannt ist. Damit ergibt sich folgende Gleichung:

$\pmatrix{\dfrac{65}{3}\\39\\z_2}=\pmatrix{27\\39\\3,5}+t\cdot \pmatrix{-13,5\\0\\-0,5}$

Mit der ersten Zeile ergibt sich $t=\dfrac{32}{81}.$ Damit lässt sich schließlich $z_2=\dfrac{535}{162}$ berechnen.

Da der Ball das Netz in einer Höhe von $0,25\,\text{ft}$ über dem Netz überquert, muss die Gleichung $\dfrac{h}{3}-\dfrac{535}{162} =0,25$ gelten.

$\begin{array}[t]{rll} 0,25&=& \dfrac{h}{3}-\dfrac{535}{162} &\quad \scriptsize \mid\; +\dfrac{535}{162} \\[5pt] 3,55&\approx& \dfrac{h}{3} &\quad \scriptsize \mid\; \cdot 3 \\[5pt] 10,65&\approx&h \end{array}$

Der gesuchte Wert für $h$ ist ungefähr $10,65.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?