Aufgabe 1A

Eine Minigolfbahn enthält als Hindernis eine Doppelwelle. Die Seitenansicht der Doppelwelle wird mit den auf $\mathbb{R}$ definierten Funktionen $f$ und $g$ modellhaft beschrieben durch

$f(x) = 0,5x^4 - 4x^3 +11x^2 -12x + 4,5$
für $1\leq x\leq 3$

und

$g(x) = 0,25x^4 - 4x^3 + 23,5x^2 - 60x + 56,25$
für $3\leq x \leq 5.$

Für $x \leq 1$ und $x \geq 5$ sind die Abschnitte der Bahn waagerecht und in der Seitenansicht durch die $x$ -Achse gegeben. Alle Angaben haben die Einheit Meter ( $\text{m}$ ). Eine dreidimensionale Ansicht der $1,25 \,\text{m}$ breiten Minigolfbahn ist in Abbildung 1 dargestellt.

Grafik eines 3D-Gitters mit Wellenform auf der x-y-Achse.

Abb. 1

Bestimme die maximale Höhe der Bahn.
Untersuche, ob der Übergang von der ersten zur zweiten Welle sprungfrei ist.
Die größte Steigung der Bahn soll den Wert $0,8$ nicht überschreiten.
Entscheide, ob die erste Welle der Minigolfbahn diese Bedingung erfüllt, und begründe deine Entscheidung.

(11 BE)

Nach einem Regenschauer steht das Wasser zwischen den beiden Wellen $5 \,\text{cm}$ hoch.
Berechne, wie viele Liter Wasser sich dort gesammelt haben.
Der Ball wird modellhaft als punktförmig angenommen. Er wird so fest geschlagen, dass er am Punkt $P(1,42\mid f(1,42))$ tangential von der Bahn abhebt. Er fliegt dann parabelförmig und erreicht seine maximale Höhe an der Stelle $x = 3$ .
Bestimme eine Funktionsgleichung, die näherungsweise die Flugparabel beschreibt.

(Zur Kontrolle: $q(x)=-0,24x^2+1,46x-1,36$ )

Zeige, dass der fliegende Ball den Hochpunkt der zweiten Welle überwindet.

(18 BE)

Das Hindernis soll im Bereich $1\leq x \leq 5$ neu gestaltet werden. Es soll aus drei jeweils $40 \, \text{cm}$ hohen Wellen bestehen und am Anfang und Ende waagerecht an den Rest der Bahn anschließen.
Bestimme hierfür eine passende Funktionsgleichung der Form

$h(x) = a\cdot \text{sin}(b\cdot x) + 0,2$ mit $a, \, b \in \mathbb{R}$ .

Das Hindernis soll seitlich verkleidet werden.
Erläutere ohne weitere Rechnung und mithilfe einer Skizze, dass der Flächeninhalt der Verkleidung auf einer der beiden Seiten durch den Term $4\cdot0,2$ berechnet werden kann.

(11 BE)

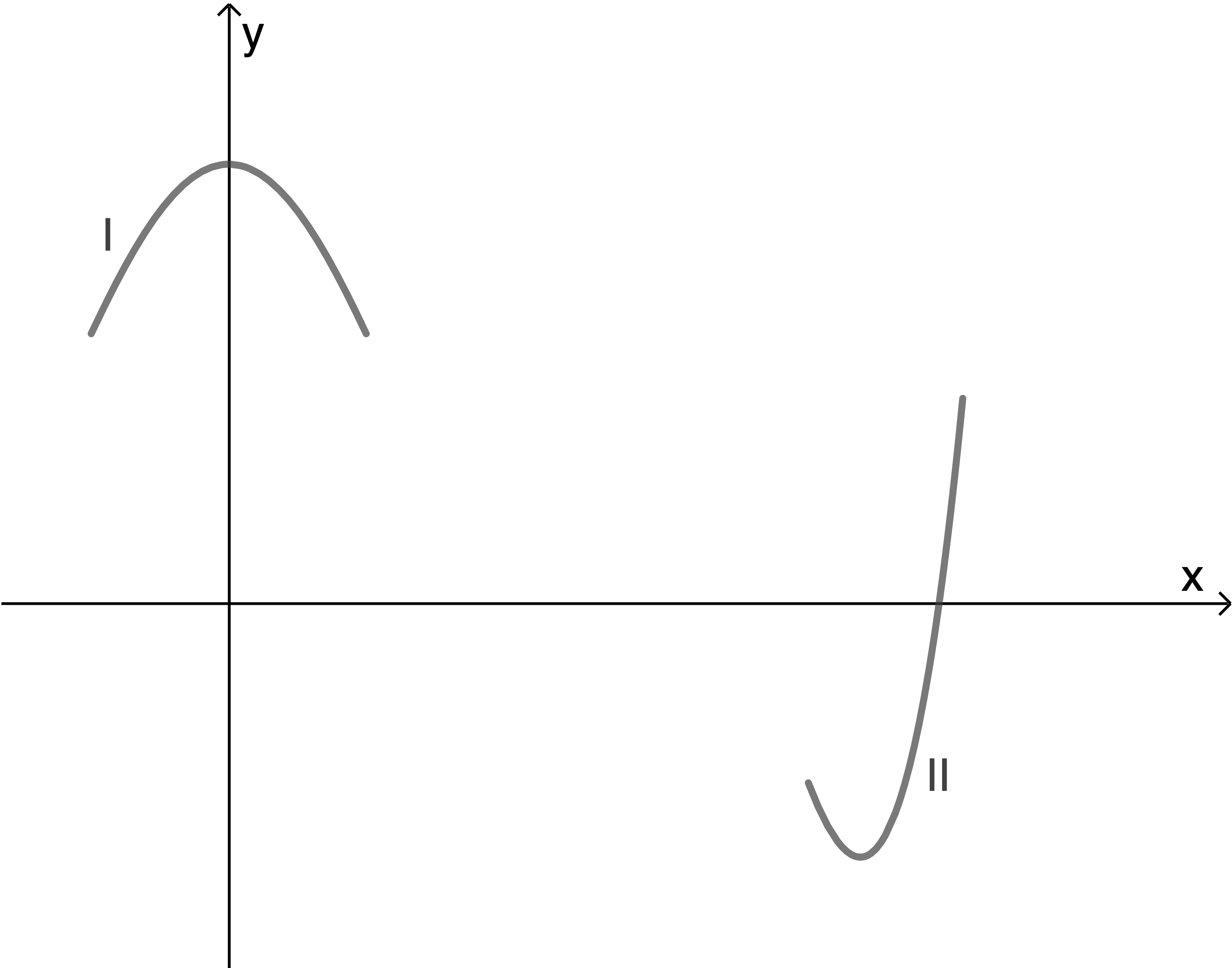
Unabhängig vom Sachzusammenhang wird die Funktionenschar $s_k$ mit

$s_k(x) = x^5 - k^2\cdot x^3+k^2\cdot x,$
$x\in\mathbb{R}$ , $k\gt0,$

betrachtet. Für einen Wert von $k$ ist ein Ausschnitt des Graphen von $s_k$ und ein Ausschnitt des zugehörigen Ableitungsgraphen in Abbildung 2 dargestellt.

Ermittle mithilfe der Abbildung und ohne weitere Rechnung die Anzahl der Nullstellen des zugehörigen vollständigen Graphen
von $s_k$ .

Grafik eines mathematischen Funktionsgraphen mit zwei sichtbaren Bereichen.

Abb. 2

(6 BE)

Maximale Höhe des Graphen der Funktion $f$ bestimmen:

Der Abbildung ist zu entnehmen, dass die maximale Höhe der Bahn im Intervall $[1;3]$ liegt.

Die maximale Höhe der Bahn entspricht dem Maximum von $f$ . Der Hochpunkt kann mit Hilfe des GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Der Hochpunkt des Graphen der Funktion $f$ befindet sich bei $H_f(2 \mid 0,5)$ .
Daraus folgt, dass die maximale Höhe der Bahn $0,5$ Meter beträgt.

Auf einen sprung-und knickfreien Übergang an der Stelle $x=3$ untersuchen:

Der Übergang der Graphen der Funktion $f$ und $g$ ist sprungfrei, wenn $f(3)=g(3)$ gilt.

$f(3)=0$

Vollständige Lösung anzeigen

$g(3)=0$

Vollständige Lösung anzeigen

Daraus folgt: $f(3)=g(3)=0$

Dadurch ist gezeigt, dass der Übergang sprungfrei ist.

Der Übergang der Graphen der Funktion $f$ und $g$ ist knickfrei, wenn $\(f$ gilt.

$\(f$

Einsetzen von $x=3$ liefert: $\(f$

$\(g$

Einsetzen von $x=3$ liefert: $\(g$

Daraus folgt: $\(f$

Dadurch ist gezeigt, dass der Übergang knickfrei ist.

Der Übergang von der ersten zur zweiten Welle an der Stelle $x=3$ ist sprung- und knickfrei.

Maximale Steigung des Graphen der Funktion $f$ ermitteln:

Die maximale Steigung des Graphen der Funktion $f$ entspricht dem Maximum der Funktion $\(f$ .
Der Hochpunkt des Graphen der Funktion $\(f$ kann mit Hilfe des GTRs bestimmt werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Der Hochpunkt des Graphen von $\(f$ liegt bei $\(H_{f$ .
Daraus folgt, dass die maximale Steigung des Graphen der Funktion $f$ $\, m=0,77$ beträgt.

Die größte Steigung der ersten Welle ist $\leq 0,8$ und daher erfüllt die erste Welle der Minigolfbahn die Bedingung.

Wassermenge berechnen:

Es gilt:

$1\,\text{l} \mathrel{\widehat{=}} 0,001\,\text{m}^3$
$5\,\text{cm}\mathrel{\widehat{=}}0,05\,\text{m}$
$V=A \cdot b$ , wobei $b$ der Breite der Minigolfbahn entspricht ( $b=1,25\,\text{m}$ ).

$f(x)=0,05$ und $g(x)=0,05$ lösen:

$\blacktriangleright$ TI 84-PLUS

Bestimme die Schnittpunkte des Graphen von $f$ und $g$ mit der Gerade zu $y = 0,05.$

2nd $\to$ trace (calc) $\to$ 5: intersect

$\blacktriangleright$ Casio fx-CG

Bestimme den $x$ -Wert zum $y$ -Wert $0,05$ mit dem X-CAL-Befehl.

F5 (G-Solv) $\to$ F6 $\to$ F2: X-CAL

$f(x)=0,05$ liefert im Intervall $[2;3]$ die Lösung $x_1\approx 2,83$ .

$g(x)=0,05$ liefert im Intervall $[3;4]$ die lösung $x_2\approx 3,26$ .

Das Wasser steht zwischen den Stellen $x_1$ und $x_2$ $5\,\text{cm}$ hoch.

Fläche $A$ berechnen:

Die Fläche, die die beiden Funktionen mit $y=0,05$ einschließen, kann mit $A= 0,05 \cdot (x_2-x_1) - \displaystyle\int_{x_1}^{3}f(x)\;\mathrm dx -\displaystyle\int_{3}^{x_2}g(x)\;\mathrm dx$ berechnet werden.

$A= 0,05 \cdot (3,26-2,83) - \displaystyle\int_{2,83}^{3}f(x)\;\mathrm dx -\displaystyle\int_{3}^{3,26}g(x)\;\mathrm dx$

Mit deinem GTR können die Integrale gelöst werden.

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

$\displaystyle\int_{2,83}^{3}f(x)\;\mathrm dx \approx 0,003$

$\displaystyle\int_{3}^{3,26}g(x)\;\mathrm dx \approx 0,005$

$A\approx 0,0135 \, [\text{m}^2]$

Vollständige Lösung anzeigen

Volumen $V$ berechnen:

$\begin{array}[t]{rll} V&=&A \cdot b \\[5pt] &=&0,0135 \, \text{m}^2 \cdot 1,25 \, \text{m} \\[5pt] &\approx&0,017 \, \text{m}^3 = 17 \, \text{l} \end{array}$

Zwischen den beiden Wellen der Minigolfbahn haben sich ungefähr $17\,\text{l}$ Wasser gesammelt.

Funktionsgleichung $q$ bestimmen:

Der Ball hebt am Punkt $P(1,42 \mid 0,22)$ ab.

Ansatz: $q(x)= ax^2 +bx +c$

Bedingungen, die erfüllt werden müssen:

$q(1,42)=f(1,42)$
$\(q$
$\(q$

1. $q(1,42)=f(1,42)$ :

$f(1,42)=0,22$ , daraus folgt, dass $q(1,42)=a \cdot 1,42^2 +b \cdot 1,42+c=0,22$ gelten muss.

2. $\(q$ :

$\(f$
$\(q$

$\(f$ , daraus folgt, dass $\(q$ gelten muss.

3. $\(q$ :

Dafür muss $\(q$ gelten.

Aus den Bedingungen kannst du ein Gleichungssystem aufstellen und anschließend kannst du dieses LGS mit Hilfe eines GTRs lösen.

$\begin{array}{lrll} \text{I}\quad&1,42^2a+1,42b+c&=& 0,22 \\ \text{II}\quad&2,84a+b&=&0,77 \\ \text{III}\quad&6a+b&=&0 \\ \end{array}$

$\blacktriangleright$ TI 84-PLUS

2ND $\rightarrow$ $x^{-1}$ $\rightarrow$ EDIT $\rightarrow$ $3x4$

In das Fenster gibst du die Zahlen aus dem linearen Gleichungssystem ein. Gib dabei zuerst die Koeffizienzen vor den Unbekannten und in der Zeile jeweils zu letzt die Zahl hinter dem Gleichheitszeichen ein:

$\pmatrix{1,42^2& 1,42& 1 & 0,22 \\ 2,84 & 1 & 0 & 0,77 \\ 6 & 1 & 0 & 0}$

Anschließend kannst du es wie folgt lösen:

2ND $\rightarrow$ $x^{-1}$ $\rightarrow$ MATH $\rightarrow$ $B$ $\rightarrow$ 2ND $\rightarrow$ MATRIX $\rightarrow$ NAMES $\rightarrow$ $1 :[A]$

$\blacktriangleright$ Casio fx-CG

Im Gleichungs-Menü:

F1: Lin. Gleichungss. $\to$ F2: 3 (Unbekannte)

Als Näherungslösungen bekommst du $a \approx -0,24$ , $b\approx 1,46$ und $c \approx -1,36$ .

Daraus folgt für die Funktionsgleichung $q$ , die näherungsweise die Flugparabel beschreibt:

$q(x)=-0,24x^2+1,46x-1,36$

Verlauf des fliegenden Balls begründen:

Aus $g(x)= q(x)$ folgt im Intervall $[3; 5]$ die einzige Lösung $x_3\approx 4,93$ (mit Hilfe eines GTRs berechnet).
Da der Graph von $g$ an der Stelle $4$ sein Maximum besitzt, überwindet der fliegende Ball den Hochpunkt der zweiten Welle.

Funktionsgleichung $h$ bestimmen:

$h(x) = a \cdot \sin(b\cdot x) +0,2$

Gesucht sind die Werte für die Parameter $a$ (Streckung in $y$ -Richtung mit dem Faktor $a$ ) und $b$ (Streckung in $x$ -Richtung mit dem Streckfaktor $\dfrac{1}{b}$ ).

Aus der Forderung, dass die Wellen $40\,\text{cm}$ hoch sein sollen, ergibt sich der Wert $a=0,2$ .

Damit genau drei Wellen in das Intervall $[1;5]$ passen, muss $b=\dfrac{2 \pi}{\frac{4}{3}} = \dfrac{3}{2} \pi$ betragen.

Daraus ergibt sich, dass für $1\leq x\leq5$ die Funktion $h(x) = 0,2 \cdot \sin\left(\dfrac{3}{2} \pi \cdot x\right) +0,2$ eine passende Funktionsgleichung ist.

Term $4 \cdot 0,2$ für den Flächeninhalt einer Seite erläutern:

Grafik eines sinusförmigen Verlaufs mit Achsen und Markierungen.

Der Flächeninhalt der Verkleidung auf einer Seite kann durch den obigen Graphen der Funktion $h$ im Intervall $[1;5]$ beschrieben werden.

Der Graph von $h$ besitzt Funktionswerte zwischen $0$ und $0,4$ und ist punktsymmetrisch zu seinen Wendepunkten. Die Flächenstücke $1$ , $2$ , $3$ , $4$ , $5$ und $6$ lassen sich jeweils genau in die Teilflächen $A$ , $B$ , $C$ , $D$ , $E$ und $F$ drehen.

Somit hat der Flächeninhalt der Verkleidung einer Seite den Wert $4 \cdot 0,2$ .

Anzahl der Nullstellen des Graphen von $s_k$ ermitteln:

Der höchste vorkommende Exponent der Funktion $s_k(x)= x^5 -k^2\cdot x^3 +k^2\cdot x$ ist $5$ . Deshalb hat die Funktion $s_k$ den Grad $5$ . Daraus folgt, dass der Graph von $s_k$ mindestens eine Nullstelle und maximal fünf Nullstellen haben kann.

Für alle Werte von $k$ verläuft der Graph von $s_k$ durch den Koordinatenursprung. Also gehört der Ausschnitt $\text{I}$ zum Ableitungsgraphen von $s_k$ und der Ausschnitt $\text{II}$ zum Graphen von $s_k$ .

Mit dem positiven Funktionswert von $\(s$ an der Stelle $x=0$ folgt, dass der Graph von $s_k$ die $x$ -Achse dort mit einem Vorzeichenwechsel von $-\rightarrow +$ schneidet.
Daraus folgt, dass der Graph von $s_k$ also zwischen dem Koordinatenursprung und der in der Abbildung dargestellten Nullstelle (siehe Ausschnitt $\text{II}$ ) noch mindestens eine weitere Nullstelle besitzt.

Da der Funktionsterm von $s_k$ nur ungerade Exponenten besitzt, ist der Graph von $s_k$ punktsymmetrisch zum Koordinatenursprung.

Daraus folgt, dass der Graph der Funktion $s_k$ mit Grad $5$ insgesamt fünf Nullstellen besitzt.