Aufgabe 3B
Für 
mit 
werden die Pyramiden 
mit 
und 
betrachtet (vgl. Abbildung 1).
Der Mittelpunkt der Strecke
ist 
.
Der Mittelpunkt der Strecke
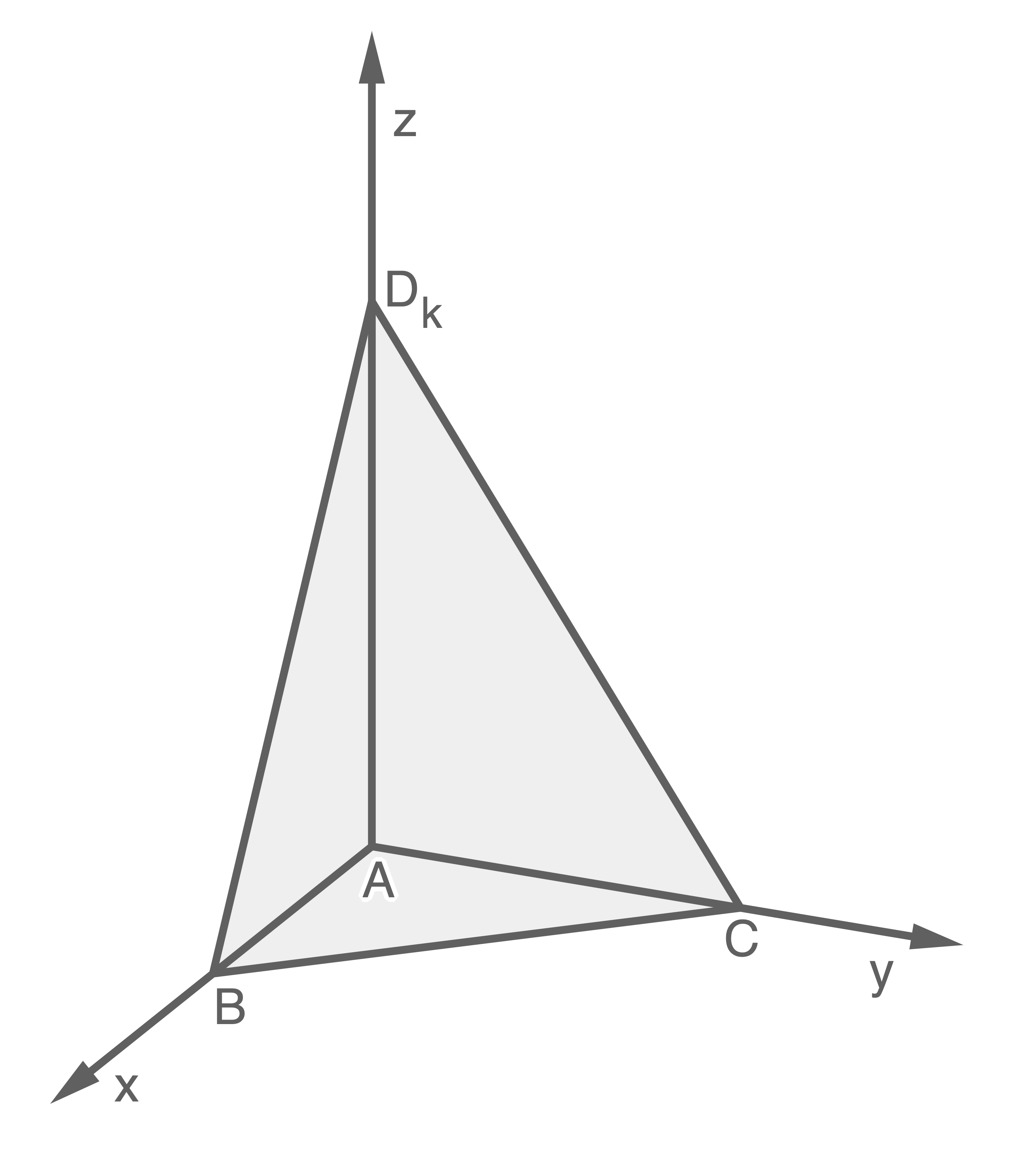
Abb. 1
a)
Begründe, dass das Dreieck 
gleichschenklig ist. Berechne den Flächeninhalt des Dreiecks für 
Für jeden Wert von
(5 BE)
b)
Bestimme eine Gleichung von 
in Koordinatenform.
[Zur Kontrolle:
]
[Zur Kontrolle:
(4 BE)
c)
Ermittle den Wert von 
, für den die Größe des Winkels, unter dem die 
-Achse die Ebene schneidet, 
beträgt.
(3 BE)
Zusätzlich zu den Pyramiden wird der in der Abbildung 2 gezeigte Quader betrachtet.
Die Punkte 
und 
sind Eckpunkte des Quaders, die Seitenflächen des Quaders sind parallel zu den Koordinatenebenen.
Für 
enthält die Seitenfläche 
der Pyramide den Eckpunkt 
des Quaders. Für kleinere Werte von schneidet die Seitenfläche den Quader in einem Vieleck.
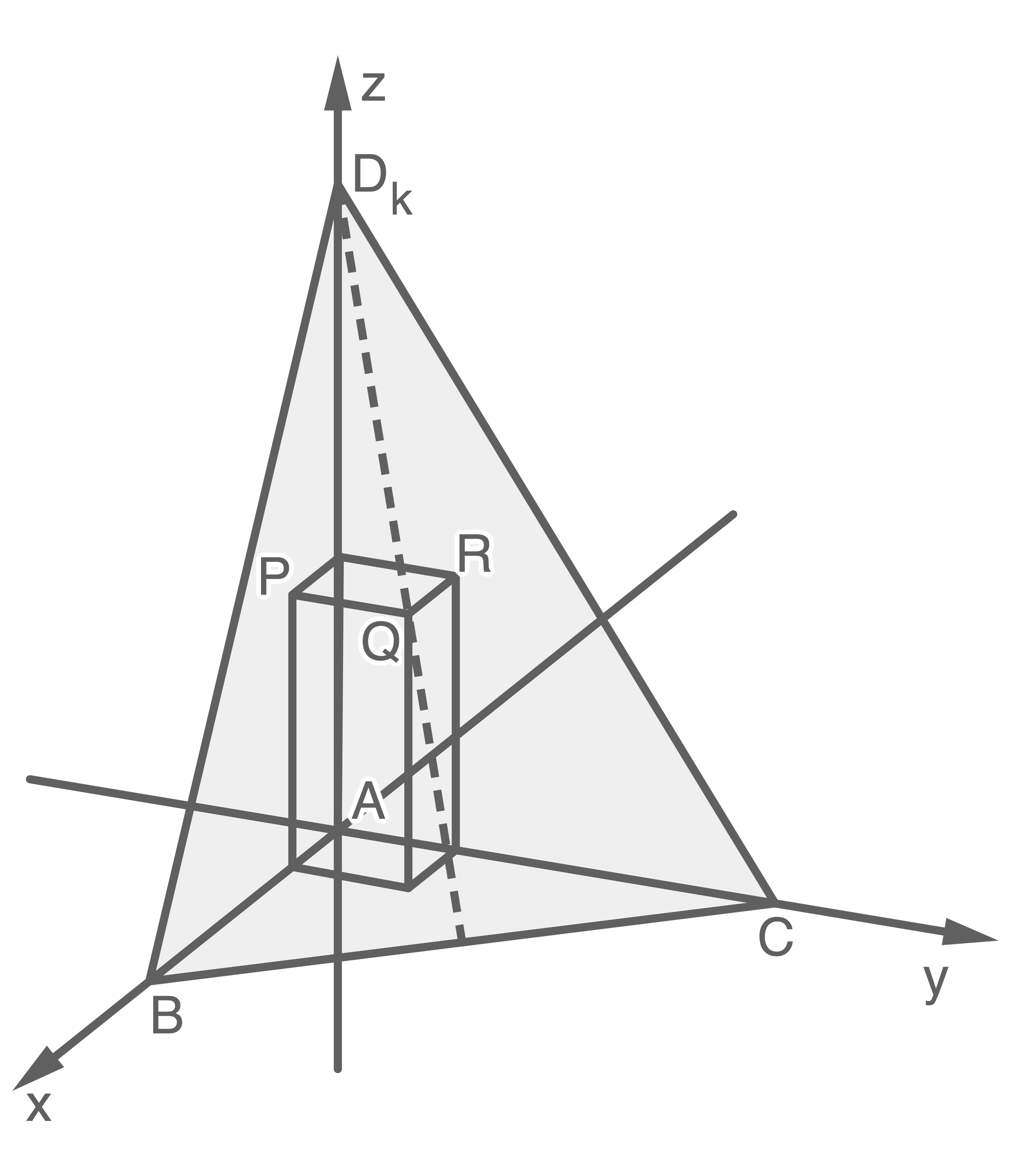
Abb. 2
d)
Für einen Wert von liegen die Eckpunkte 
und 
des Quaders in der Seitenfläche .
Bestimme diesen Wert von
[Zur Kontrolle: 
]
Für diesen Wert von liegt ein Punkt einer vorderen Kante ebenfalls in der Seitenfläche .
Bestimme die Koordinaten dieses Punktes.
Bestimme diesen Wert von
Für diesen Wert von
Bestimme die Koordinaten dieses Punktes.
(6 BE)
e)
Gib in Abhängigkeit von die Anzahl der Eckpunkte des Vielecks an, in dem die Seitenfläche den Quader schneidet.
(3 BE)
f)
Nun wird die Pyramide 
betrachtet. Dieser Pyramide werden Quader einbeschrieben (vgl. Abbildung 3). Die Grundflächen der Quader liegen in der 
-Ebene, haben den Eckpunkt gemeinsam und sind quadratisch. Die Höhe 
der Quader durchläuft alle reellen Werte mit 
. Für jeden Wert von liegt der Eckpunkt 
in der Seitenfläche 
der Pyramide.
Ermittle die Koordinaten des Punkts 
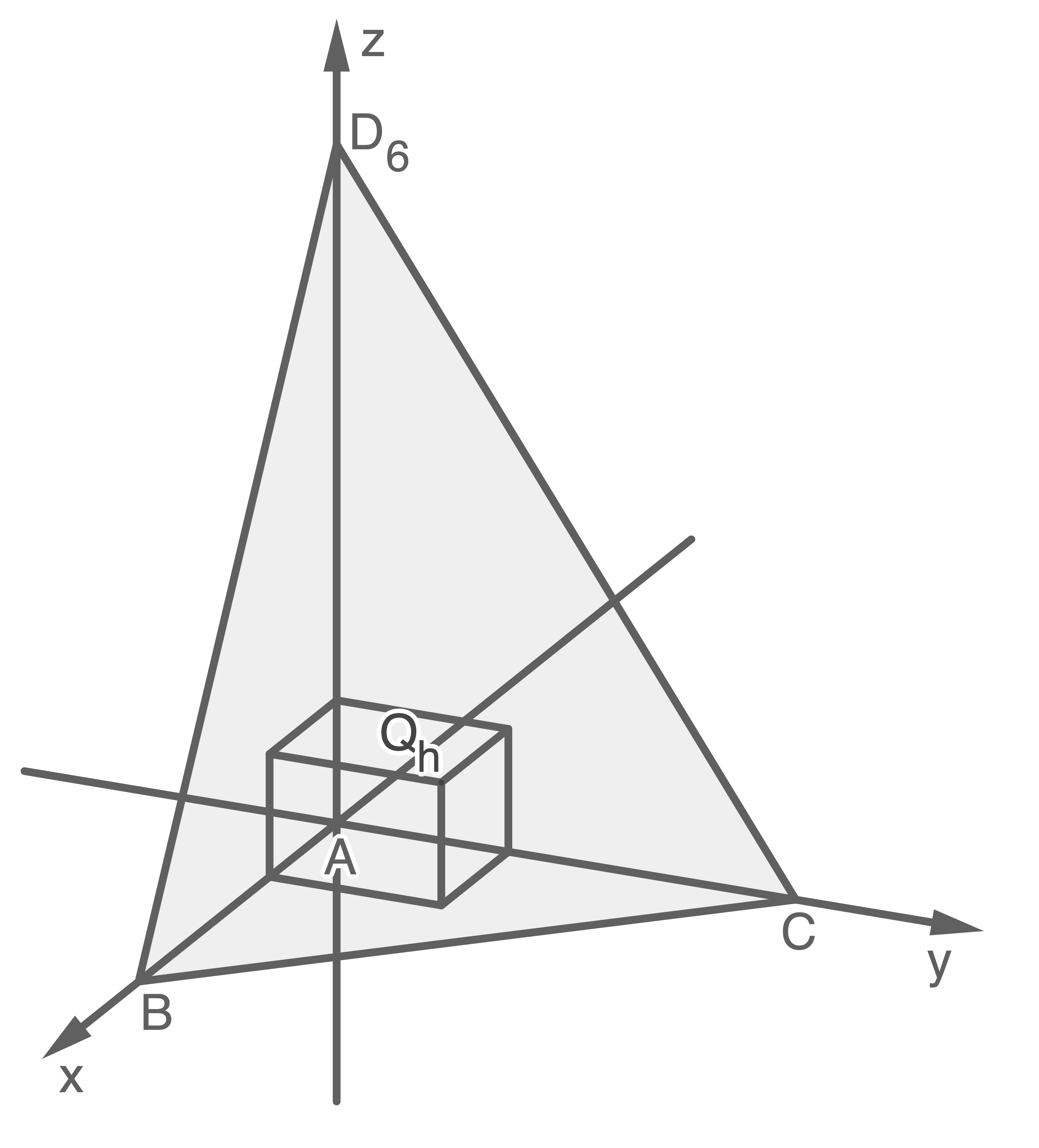
Abb. 3
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Die Höhe des Dreiecks beträgt:
b)
Ansatz für die Koordinatenform: 
Einsetzen der Koordinaten von 
und 
führt auf folgendes LGS:
Wähle 
, dann ist 
, 
und 
Somit folgt eine mögliche Ebenengleichung mit : 
c)
Richtungsvektor der -Achse: 
Normalenvektor von 
![\(\begin{array}[t]{rll}
\sin \left(30^{\circ}\right)&=& \dfrac{\vec{r} \cdot \overrightarrow{n_{k}}}{|\vec{r}| \cdot |\overrightarrow{n_{k}}|} \\[5pt]
0,5 &=& \dfrac{\dfrac{k}{4}}{1 \cdot \sqrt{1+1+\frac{16}{k^{2}}}} &\quad \scriptsize \mid\; \cdot 4 \cdot \sqrt{1+1+\frac{16}{k^{2}}} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d80d4cbbe2909679de58de1a45007e095994bff3c75a9aa6a36470ee4e06b053?color=5a5a5a)
Lösen mit dem Taschenrechner ergibt: 
d)
Der Zeichnung entnimmt man, dass dieselben 
- und -Koordinaten wie hat: 
Die Punktprobe mit P ergibt:
![\(\begin{array}[t]{rll}
1+0+\dfrac{4}{k} \cdot 3 &=& 4 \\[5pt]
1+\dfrac{12}{k} &=& 4 &\quad \scriptsize \mid\; -1 \\[5pt]
\dfrac{12}{k} &=& 3 &\quad \scriptsize \mid\; \cdot \dfrac{k}{3} \\[5pt]
4 &=& k \\
k &=& 4 \\
\end{array}\)](https://mathjax.schullv.de/144ec7dbedf9ab136cffc0e6a913a78b1ef77822df44452c7be3824923bcb1fa?color=5a5a5a)
Der gesuchte Punkt hat die Koordinaten 
mit 
. Einsetzen der Koordinaten in die Gleichung für 
liefert:
![\(\begin{array}[t]{rll}
1+1+1 \cdot h &=& 4 &\quad \scriptsize \mid\; -2 \\[5pt]
h &=& 2
\end{array}\)](https://mathjax.schullv.de/8cdbaae66d7ca7b509dbc2683ed56e34bab466fb9cd6632562ff869da3b5d502?color=5a5a5a)
Somit lauten die Koordinaten des Punkts 
e)
: vier Eckpunkte
: fünf Eckpunkte
: drei Eckpunkte
f)
Jeder Punkt 
liegt auf der Strecke 
. Diese wird beschrieben durch:
hat die -Koordinate , also gilt
![\(\begin{array}[t]{rll}
h &=& 6 \cdot s &\quad \scriptsize \mid\; :6 \\[5pt]
\dfrac{h}{6} &=& s
\end{array}\)](https://mathjax.schullv.de/9ef0c9ebd4b8e5a618f688ffb95c71d762404013da682c0adf20f281c9d4207b?color=5a5a5a)
Für die 
Koordinate gilt:
![\(\begin{array}[t]{rll}
x&=& 2 + s \cdot (-2) \\[5pt]
x&=& 2 + \dfrac{h}{6} \cdot (-2) \\[5pt]
x&=& 2 - \dfrac{h}{3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a6023e3d192fb58fd45d00b8bf58e4749c2dd81574e1e331354c19671a232819?color=5a5a5a)
Die gleiche Rechnugn folgt für die 
Koordinate:
![\(\begin{array}[t]{rll}
y&=& 2 + s \cdot (-2) \\[5pt]
y&=& 2 + \dfrac{h}{6} \cdot (-2) \\[5pt]
y&=& 2 - \dfrac{h}{3} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/af0461b4aecae98de21e6ffecfd130eefcc70cf52cdcce42a7d01a643fe3f58d?color=5a5a5a)
Folglich hat der Punkt die Koordinaten: 