Aufgabe 1A
Die auf  definierte Funktion
definierte Funktion  mit
mit  modelliert für
modelliert für  die Konzentration eines Medikamentenwirkstoffes im Blut. Dabei beschreibt
die Konzentration eines Medikamentenwirkstoffes im Blut. Dabei beschreibt  die Zeit in Stunden (
die Zeit in Stunden ( ) nach der Einnahme des Medikamentes und
) nach der Einnahme des Medikamentes und  die Konzentration in Milligramm pro Liter
die Konzentration in Milligramm pro Liter  .
.
 mit
mit 
 gegeben.
gegeben.
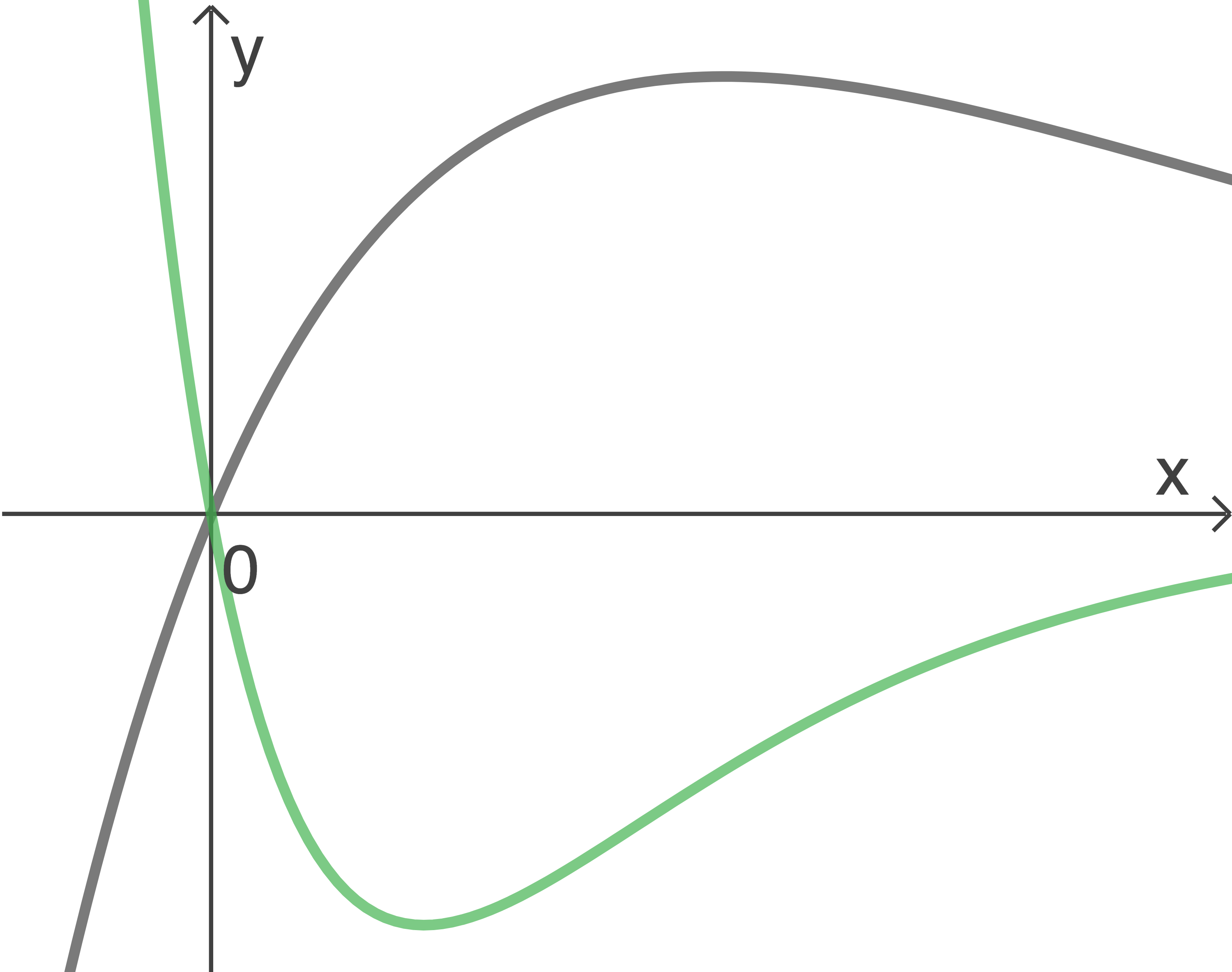
In der Abbildung sind zwei Graphen der Schar dargestellt. Jeder Graph der Funktionenschar hat genau einen Extrempunkt. Eine Stammfunktion von ist durch
ist durch  gegeben.
gegeben.
a)
Berechne die Konzentration eine Stunde nach der Einnahme des Medikamentes. Gib den Zeitpunkt an, zu dem die Konzentration erstmals den Wert  annimmt.
annimmt.
Bestimme, wie lange die Konzentration mindestens beträgt.
beträgt.
Bestimme, wie lange die Konzentration mindestens
(6 BE)
b)
Zeige rechnerisch, dass die Konzentration ungefähr  Stunden nach der Einnahme des Medikamentes mit etwa
Stunden nach der Einnahme des Medikamentes mit etwa  am größten ist.
am größten ist.
(4 BE)
c)
Bestimme den Zeitpunkt, zu dem die Konzentration genauso groß ist wie zwei Stunden später.
(3 BE)
d)
Bestimme die Lösung der Gleichung  und interpretiere die Lösung im Sachzusammenhang.
und interpretiere die Lösung im Sachzusammenhang.
(4 BE)
e)
Eine vereinfachte Modellierung geht davon aus, dass bis  Stunden nach der Einnahme des Medikamentes die Konzentration durch
Stunden nach der Einnahme des Medikamentes die Konzentration durch  beschrieben wird und danach die Abnahmerate der Konzentration konstant ist. Dabei ist die konstante Abnahmerate so groß wie die Änderungsrate der durch
beschrieben wird und danach die Abnahmerate der Konzentration konstant ist. Dabei ist die konstante Abnahmerate so groß wie die Änderungsrate der durch  beschriebenen Konzentration nach
beschriebenen Konzentration nach  Stunden.
Stunden.
Bestimme den Zeitpunkt nach der Einnahme des Medikamentes, zu dem die Konzentration nach diesem Modell null ist.
Bestimme den Zeitpunkt nach der Einnahme des Medikamentes, zu dem die Konzentration nach diesem Modell null ist.
(4 BE)
f)
Vier Stunden nach der ersten Einnahme wird das Medikament in der gleichen Dosierung erneut eingenommen. Die Gesamtkonzentration ist zu jedem Zeitpunkt die Summe der durch  beschriebenen Konzentration, die sich aus der ersten und zweiten Einnahme ergeben. Die Gesamtkonzentration soll
beschriebenen Konzentration, die sich aus der ersten und zweiten Einnahme ergeben. Die Gesamtkonzentration soll  nicht übersteigen.
nicht übersteigen.
Untersuche, ob diese Vorgabe eingehalten wird.
Unabhängig vom Sachzusammenhang ist die Funktionenschar Untersuche, ob diese Vorgabe eingehalten wird.
(4 BE)
In der Abbildung sind zwei Graphen der Schar dargestellt. Jeder Graph der Funktionenschar hat genau einen Extrempunkt. Eine Stammfunktion von

g)
Berechne die Werte von  , für die die Fläche zwischen dem Graph von
, für die die Fläche zwischen dem Graph von  und der
und der  -Achse im Intervall
-Achse im Intervall ![\([0;1]\)](https://mathjax.schullv.de/67b85eab103aec1314a6a9fe5de4b047f5cd37fb49f90a88e9c8c39a6daa39b6?color=5a5a5a) den Inhalt
den Inhalt  hat.
hat.
(4 BE)
h)
Entscheide, für welche Werte von  an der Extremstelle ein Maximum und für welche ein Minimum vorliegt.
an der Extremstelle ein Maximum und für welche ein Minimum vorliegt.
Begründe deine Entscheidung ohne Berechnung der Extremstelle.
Begründe deine Entscheidung ohne Berechnung der Extremstelle.
(6 BE)
i)
Der Graph von  wird an der
wird an der  -Achse gespiegelt.
-Achse gespiegelt.
Berechne die Werte von , für die sich der gespiegelte Graph und der Graph
, für die sich der gespiegelte Graph und der Graph  unter einem rechten Winkel schneiden.
unter einem rechten Winkel schneiden.
Berechne die Werte von
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Konzentration eine Stunde nach Einnahme
 Zeitpunkt bestimmen
Es soll gelten:
Zeitpunkt bestimmen
Es soll gelten:
 Mit dem solve-Befehl des Taschenrechners ergibt sich, dass die Konzentration nach ungefähr einer Viertelstunde erstmals den Wert
Mit dem solve-Befehl des Taschenrechners ergibt sich, dass die Konzentration nach ungefähr einer Viertelstunde erstmals den Wert  annimmt.
Intervall bestimmen
Es soll
annimmt.
Intervall bestimmen
Es soll  gelten.
Mit dem solve-Befehl wird die Gleichnug
gelten.
Mit dem solve-Befehl wird die Gleichnug  gelöst.
Daraus ergeben sich die Werte
gelöst.
Daraus ergeben sich die Werte  und
und 
 erfüllt
erfüllt 
 Die Konzentration beträgt ungefähr 7,67 Stunden mindestens
Die Konzentration beträgt ungefähr 7,67 Stunden mindestens 
b)
Die Konzentration soll nach  Stunden am höchsten sein, gesucht ist also das Maximum von
Stunden am höchsten sein, gesucht ist also das Maximum von  in
in ![\([0;12].\)](https://mathjax.schullv.de/24d7e2faf185629ed359b5769ee46138cb08c8d67cff7c845b1813bff58b4554?color=5a5a5a) 1. Schritt: Ableitungen aufstellen
1. Schritt: Ableitungen aufstellen

 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/a4bb39e23662782534070270398b1e04e1158b0c34e6260f10edc859bf7dd457?color=5a5a5a) Diese Gleichung wird mit dem solve-Befehl des Taschenrechners gelöst.
Es ergibt sich
Diese Gleichung wird mit dem solve-Befehl des Taschenrechners gelöst.
Es ergibt sich  3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Also befindet sich das Maximum an der Stelle
3. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Also befindet sich das Maximum an der Stelle  4. Schritt: Funktionswert berechnen und Intervallränder überprüfen
4. Schritt: Funktionswert berechnen und Intervallränder überprüfen





 Die Konzentration ist ca.
Die Konzentration ist ca.  Stunden nach der Einnahme mit etwa
Stunden nach der Einnahme mit etwa  am größten.
am größten.
c)
Gesucht ist die Lösung der Gleichung:
Mit dem solve-Befehl des Taschenrechners ergibt sich  Ungefähr 0,2 Stunden nach der Einnahme ist die Konzentration genauso groß wie zwei Stunden später.
Ungefähr 0,2 Stunden nach der Einnahme ist die Konzentration genauso groß wie zwei Stunden später.
d)
Es gilt:
Lösen dieser Gleichung mit dem solve-Befehl des Taschenrechners ergibt:  Die Ableitung
Die Ableitung  gibt die momentane Änderungsrate an der Stelle
gibt die momentane Änderungsrate an der Stelle  an, während der Term
an, während der Term  die durchschnittliche Änderungsrate zwischen den Stellen
die durchschnittliche Änderungsrate zwischen den Stellen  und
und  angibt.
Im Sachzusammenhang bedeutet die Gleichung, dass die momentane Änderungsrate der Medikamentenkonzentration nach ungefähr 2,3 Stunden genauso groß ist, wie die durchschnittliche Änderungsrate zwischen den Zeitpunkten
angibt.
Im Sachzusammenhang bedeutet die Gleichung, dass die momentane Änderungsrate der Medikamentenkonzentration nach ungefähr 2,3 Stunden genauso groß ist, wie die durchschnittliche Änderungsrate zwischen den Zeitpunkten  und
und 
e)
Die Konzentration für  wird durch die Tangente des Graphen von
wird durch die Tangente des Graphen von  durch den Punkt
durch den Punkt  beschrieben.
1. Schritt: Tangentengleichung aufstellen
Dafür wird zunächst der Funktionswert und die Steigung bei
beschrieben.
1. Schritt: Tangentengleichung aufstellen
Dafür wird zunächst der Funktionswert und die Steigung bei  berechnet.
berechnet.



 Mit diesen Werten kann die Tangentengleichung aufgestellt werden:
Mit diesen Werten kann die Tangentengleichung aufgestellt werden:
 2. Schritt: Nullstelle der Tangente berechnen
Es gilt
2. Schritt: Nullstelle der Tangente berechnen
Es gilt  . Die Nullstelle wird über den solve-Befehl des Taschenrechners ermittelt.
Die Lösung ist
. Die Nullstelle wird über den solve-Befehl des Taschenrechners ermittelt.
Die Lösung ist  Ungefähr
Ungefähr  Stunden nach der Einnahme ist die Konzentration nach diesem Modell gleich Null.
Stunden nach der Einnahme ist die Konzentration nach diesem Modell gleich Null.
f)
Die Gesamtkonzentration wird durch die Funktion  für
für  beschrieben.
beschrieben.
Es soll für
für  gelten. Zur Überprüfung wird graphisch das Maximum von
gelten. Zur Überprüfung wird graphisch das Maximum von  mit dem Taschenrechner bestimmt.
Die Koordinaten des Hochpunktes sind ungefähr gegeben durch
mit dem Taschenrechner bestimmt.
Die Koordinaten des Hochpunktes sind ungefähr gegeben durch  Damit liegt der maximale Funktionswert bei
Damit liegt der maximale Funktionswert bei  Die Vorgabe wird also eingehalten.
Die Vorgabe wird also eingehalten.
Es soll
g)
An der Abbildung ist erkennbar, dass die Graphen der Funktionenschar  nur die Nullstelle
nur die Nullstelle  besitzen. Die Graphen von
besitzen. Die Graphen von  verlaufen also im Intervall
verlaufen also im Intervall ![\([0;1]\)](https://mathjax.schullv.de/67b85eab103aec1314a6a9fe5de4b047f5cd37fb49f90a88e9c8c39a6daa39b6?color=5a5a5a) entweder nur oberhalb oder unterhalb der
entweder nur oberhalb oder unterhalb der  -Achse.
Gesucht ist also ein Wert für
-Achse.
Gesucht ist also ein Wert für  sodass
sodass  gilt.
Nach Aufgabenstellung ist bereits eine Stammfunktion
gilt.
Nach Aufgabenstellung ist bereits eine Stammfunktion  gegeben. Damit ergibt sich:
Diese Gleichung kann mit dem solve-Befehl des Taschenrechners gelöst werden.
Für
gegeben. Damit ergibt sich:
Diese Gleichung kann mit dem solve-Befehl des Taschenrechners gelöst werden.
Für  ergibt sich die Lösung
ergibt sich die Lösung  und für
und für  die Lösung
die Lösung 
h)
Es gilt  und
und 
Der Abbildung kann entnommen werden, dass ein Maximum vorliegt, wenn für
für  und ein Minimum vorliegt, wenn
und ein Minimum vorliegt, wenn  für
für  ist.
Es muss dementsprechend untersucht werden, für welche Werte
ist.
Es muss dementsprechend untersucht werden, für welche Werte  die Schar
die Schar  positiv bzw. negativ ist.
Ist
positiv bzw. negativ ist.
Ist  und
und  , so gilt
, so gilt  . Damit ist
. Damit ist 
Ist und
und  , gilt
, gilt  . Somit ist
. Somit ist  Für
Für  nimmt
nimmt  an der Extremstelle ein Maximum an und für
an der Extremstelle ein Maximum an und für  ein Minimum.
ein Minimum.
Der Abbildung kann entnommen werden, dass ein Maximum vorliegt, wenn
Ist
i)
Wird der Graph von  an der
an der  -Achse gespiegelt, ergibt sich die Funktion
-Achse gespiegelt, ergibt sich die Funktion  1. Schritt: Schnittstelle berechnen
1. Schritt: Schnittstelle berechnen
![\(\begin{array}[t]{rll}
f_a(x)&=&g_a(x) &\quad \scriptsize \\[5pt]
\mathrm{e}^{-a \cdot x}-\mathrm{e}^{-4x}&=&-\mathrm{e}^{-a \cdot x}+\mathrm{e}^{-4x}
\end{array}\)](https://mathjax.schullv.de/118966db08b111ac705cc4601c2a2e0f24f4e9b12a3ffdac86fc1d1253779b10?color=5a5a5a) Mit dem solve-Befehl des Taschenrechners ergibt sich, dass sich die Graphen von
Mit dem solve-Befehl des Taschenrechners ergibt sich, dass sich die Graphen von  und von
und von  an der Stelle
an der Stelle  schneiden.
2. Schritt: Ableitungen bilden
Es gilt:
schneiden.
2. Schritt: Ableitungen bilden
Es gilt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/ded893a64a64870928bedf812a28a114727e75c316effe8cb6b29653f9778e73?color=5a5a5a) 3. Schritt: Wert für
3. Schritt: Wert für  ermitteln
Der gespiegelte Graph und der Graph von
ermitteln
Der gespiegelte Graph und der Graph von  schneiden sich nur im Ursprung. Damit sich die Graphen im Ursprung senkrecht schneiden, muss
schneiden sich nur im Ursprung. Damit sich die Graphen im Ursprung senkrecht schneiden, muss  gelten.
Mit der
gelten.
Mit der  -Formel ergibt sich:
-Formel ergibt sich:
![\(\begin{array}[t]{rll}
a_{1/2}&=& -\dfrac{-8}{2}\pm \sqrt{\left(\dfrac{-8}{2} \right)^2-15} \\[5pt]
&=& 4\pm 1
\end{array}\)](https://mathjax.schullv.de/4d5183a132e52a166927f8c2f54dacf50ebe2f193982f6460254f81526ab2be6?color=5a5a5a) Es ergibt sich
Es ergibt sich  und
und  Für diese Werte von
Für diese Werte von  schneiden sich der gespiegelte Graph und der Graph von
schneiden sich der gespiegelte Graph und der Graph von  unter einem rechten Winkel im Ursprung.
unter einem rechten Winkel im Ursprung.