Aufgabe A2
a)
 Wahrscheinlichkeit berechnen
Wahrscheinlichkeit berechnen
In dieser Aufgabe sollst du die Wahrscheinlichkeit

dafür berechnen, dass der Spieler mit zwei Würfen die Punktzahl

erreicht. Ein Spieler kann hierbei nur die Punktzahl

erreichen, wenn er eine

und anschließend eine

würfelt. Falls der Spieler zuerst eine

würfelt hätte der Spieler gewonnen und das Spiel wäre beendet.
Die einzige Möglichkeit ist somit, dass der Spieler zuerst eine

würfelt und anschließend eine

. Die Wahrscheinlichkeit eine

zu würfeln liegt hierbei bei

und eine

zu würfeln bei

. Somit ergibt sich mit der Pfadregel folgende Wahrscheinlichkeit:
Somit beträgt die Wahrscheinlichkeit dafür, dass ein Spieler mit zwei Würfen die Punktzahl

erreicht

.
b)

 -Werte begründen
-Werte begründen
In dieser Teilaufgabe sollst du begründen, dass

nur die Werte

,

,

oder

annehmen kann.

gibt hierbei den an den Spieler ausgezahlten Betrag in Euro an.
Der Spieler kann in einem Spiel verlieren oder gewinnen. Verliert der Spieler bekommt er

Euro ausgezahlt. Gewinnt der Spieler bekommt er pro Wurf in diesem Spiel

Euro ausgezahlt. Hierbei musst du beachten, dass ein Spieler nur dann gewinnt, wenn er genau die Punktzahl

erreicht. Du musst dir also überlegen, welche Möglichkeiten es gibt, dass ein Spieler genau die Punktzahl

erreicht.
Eine Möglichkeit besteht darin, dass der Spieler beim ersten Wurf die Punktzahl

würfelt. Somit würde der Spieler einen Betrag von

Euro ausgezahlt bekommen, da er nur einmal gewürfelt hat.
Eine weitere Möglichkeit ist, dass der Spieler zweimal die Punktzahl

würfelt. Somit würde der Spieler

Euro ausgezahlt bekommen, da er zweimal gewürfelt hat.
Die letzte Möglichkeit ist, dass der Spieler fünfmal die Punktzahl

würfelt. Dadurch würde der Auszahlungsbetrag auf

Euro ansteigen.
Dies sind alle Möglichkeiten, die für den Auszahlungsbetrag auftreten können. Deshalb kann

nur die Werte

,

,

oder

annehmen.
 Begründen, dass das Spiel nicht fair ist
Begründen, dass das Spiel nicht fair ist
In dieser Teilaufgabe sollst du begründen, dass das Spiel nicht fair ist. Dazu musst du den Erwartungswert berechnnen. Den Erwartungswert lässt sich mit folgender Formel berechnen:

bezeichnet hierbei den ausgezahlten Betrag in Euro. Zuerst kannst du somit den Erwartungswert für den ausgezahlten Betrag berechnen. Um zu begründen, dass das Spiel nicht fair ist musst du anschließend noch den Einsatz von

Euro abziehen. Damit das Spiel fair ist muss

gelten.
Für den Erwartungswert des Spiels folgt mit der angegeben Wahrscheinlichkeitsverteilung und dem Einsatz

:
Somit beträgt der Erwartungswert

und dies ist ungleich Null. Deshalb ist das Spiel nicht fair.
 Auszahlungsbetrag verändern
Auszahlungsbetrag verändern
In dieser Teilaufgabe sollst du untersuchen, ob bei einem unveränderten Einsatz von

der Auszahlungsbetrag pro Wurf so verändert werden kann, dass das Spiel fair ist. Bezeichne hierbei den Auszahlungsbetrag pro Wurf mit

. Nun musst du den Auszahlungsbetrag pro Wurf abändern, sodass

gilt. Stelle dazu den Erwartungswert in Abhängigkeit des Auszahlungsbetrags dar und löse nach

auf.
Somit gilt für einen Auszahlungsbetrag von

, dass das Spiel fair ist.
c)
 Wahrscheinlichkeit bestimmen
Wahrscheinlichkeit bestimmen
In dieser Teilaufgabe sollst du die Wahrscheinlichkeit dafür betimmen, dass der Spieler von

Spielen mindestens

und höchstens

gewinnt. Somit ist die gesuchte Wahrscheinlichkeit

. Die Wahrscheinlichkeit, dass ein Spieler verliert liegt bei

. Entsprechend gilt für die Wahrscheinlichkeit

, dass ein Spieler gewinnt mit dem Gegenereigniss:
![\(\begin{array}[t]{rll}
p &=& 1 - P(X=0)\\[5pt]
&=& 1 - \dfrac{349}{486}\\[5pt]
&=& \dfrac{137}{486}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/5b87d66e6160fd95ef2b46c75f8a5054db4e3e4fa4bcec0ba9194b0e3a5abc71?color=5a5a5a)
Du kannst hierbei nun die gesuchte Wahrscheinlichkeit mit der Binomialverteilung berechnen. Die Wahrscheinlichkeit

kannst du außerdem wie folgt umschreiben:
Zudem ist gegeben, dass der Spieler insgessamt

Spiele spielt. Verwende den binomcdf-Befehl deines GTR. Diesen findest du unter
2ND

VARS(DISTR)

B: binomcdf.
Für die Wahrscheinlichkeiten folgt mit deinem GTR:
Somit beträgt die Wahrscheinlichkeit, dass der Spieler von

Spielen mindestens

und höchstens

gewinnt

.
 Wahrscheinlichkeit erläutern
Wahrscheinlichkeit erläutern
In dieser Teilaufgabe sollst du erläutern welche Wahrscheinlichkeit mit dem Term

berechnet werden kann. Der Term

gibt hierbei die Wahrscheinlichkeit dafür an, dass ein Spieler von

Spielen einmal verliert und

-mal gewinnt. Dies lässt sich auch durch die folgende Formel zur Berechnung der Wahrscheinlichkeit bei einer Binomialverteilung verdeutlichen:
In diesem Fall gilt

,

und

.
Der gesamte Term

bezeichnet das Gegenereignis des Terms

. Somit berechnet der gegebene Term die Wahrcheinlichkeit dafür, dass ein Spieler von

Spielen nicht einmal verliert und nicht

-mal gewinnt.
d)
 Gleichung herleiten
Gleichung herleiten
In dieser Aufgabe sollst du eine Gleichung zur Bestimmung der Anzahl aller Kugeln in einer Urne herleiten. Hierfür hast du gegeben, dass sich neben anderen Kugeln genau fünf gelbe Kugeln befinden. Außerdem ist bekannt, dass wenn zwei Kugeln gleichzeitig aus der Urne gezogen werden, die Wahrscheinlichkeit eine gelbe zu bekommen

beträgt. Du kannst hierbei zur Hilfe ein zweistufiges Baumdiagramm zeichnen mit den Pfaden gelb oder nicht gelb.
Bezeichne hierbei die Gesamtanzahl aller Kugeln in einer Urne mit

. Somit folgt für die gesamte Anzahl aller nicht gelben Kugeln

, da in der Urne genau

gelbe Kugeln sind. Es handelt sich hierbei um Ziehen ohne Zurücklegen. Das bedeutet, dass sich beim zweiten Ziehen nur noch

Kugeln in der Urne befinden.
Das Baumdiagramm mit den einzelnen Wahrscheinlichkeiten ergibt sich dann wie folgt:
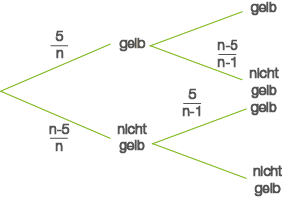 Abb. 3: Baumdiagramm
Abb. 3: Baumdiagramm
Du hast in der Aufgabenstellung die Wahrscheinlichkeit dafür gegeben, dass eine der beiden gezogenen Kugeln gelb ist. Hierfür gibt es zwei Möglichkeiten, da du zuerst eine Kugel ziehen kannst, die nicht gelb ist und anschließend eine gelbe Kugel oder zuerst eine gelbe Kugel und anschließend eine nicht gelbe Kugel.
Für die Wahrscheinlichkeit

, dass beim Ziehen von zwei Kugeln eine der beiden Kugeln gelb ist folgt somit:
Da du hierbei gegeben hast, dass

gilt, folgt der Term

für die Gesamtanzahl

an Kugeln in der Urne.
Bildnachweise [nach oben]
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
erreicht.
erreicht oder ein „V“ würfelt.
 erreicht.
erreicht.
 nur die Werte
nur die Werte  ,
,  ,
,  oder
oder  annehmen kann.
Begründe, dass das Spiel nicht fair ist.
Untersuche, ob bei unverändertem Einsatz von einem Euro der Auszahlungsbetrag pro Wurf so verändert werden kann, dass das Spiel fair wird.
annehmen kann.
Begründe, dass das Spiel nicht fair ist.
Untersuche, ob bei unverändertem Einsatz von einem Euro der Auszahlungsbetrag pro Wurf so verändert werden kann, dass das Spiel fair wird.
 Spielen mindestens
Spielen mindestens  und höchstens
und höchstens  gewinnt.
Erläutere, welche Wahrscheinlichkeit im Sachzusammenhang des Spiels ‚Die goldene Zehn‘ mit dem Term
gewinnt.
Erläutere, welche Wahrscheinlichkeit im Sachzusammenhang des Spiels ‚Die goldene Zehn‘ mit dem Term  berechnet werden kann.
berechnet werden kann.
.
 VARS(DISTR)
VARS(DISTR)  B: binomcdf.
B: binomcdf.
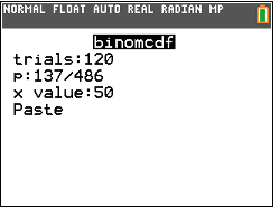 Abb. 1: Eingetragene Daten
Abb. 1: Eingetragene Daten
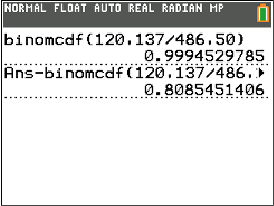 Abb. 2: Ergebnis
Abb. 2: Ergebnis
 Abb. 3: Baumdiagramm
Abb. 3: Baumdiagramm
 STAT
STAT  DIST
DIST  BINM
BINM  Bcd.
Bcd.
 Abb. 1: Ergebnis 1
Abb. 1: Ergebnis 1
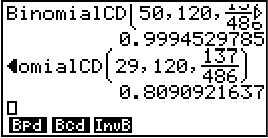 Abb. 2: Ergebnis 2
Abb. 2: Ergebnis 2
 Abb. 3: Baumdiagramm
Abb. 3: Baumdiagramm