Aufgabe 1C
Ein ICE fährt bis 15:00 Uhr mit konstanter Geschwindigkeit. Von 15:00 Uhr bis 15:02 Uhr nimmt seine Geschwindigkeit ab. Ab 15:02 Uhr fährt der ICE wieder mit konstanter Geschwindigkeit.
Die Geschwindigkeit von 15:00 Uhr bis 15:02 Uhr wird mithilfe der in definierten Funktion
definierten Funktion  mit
mit  beschrieben.
beschrieben.
Dabei ist die seit 15:00 Uhr vergangene Zeit in Minuten und
die seit 15:00 Uhr vergangene Zeit in Minuten und  die Geschwindigkeit in Kilometer pro Stunde. Abbildung 1 veranschaulicht den Sachverhalt.
die Geschwindigkeit in Kilometer pro Stunde. Abbildung 1 veranschaulicht den Sachverhalt.
Die Geschwindigkeit von 15:00 Uhr bis 15:02 Uhr wird mithilfe der in
Dabei ist
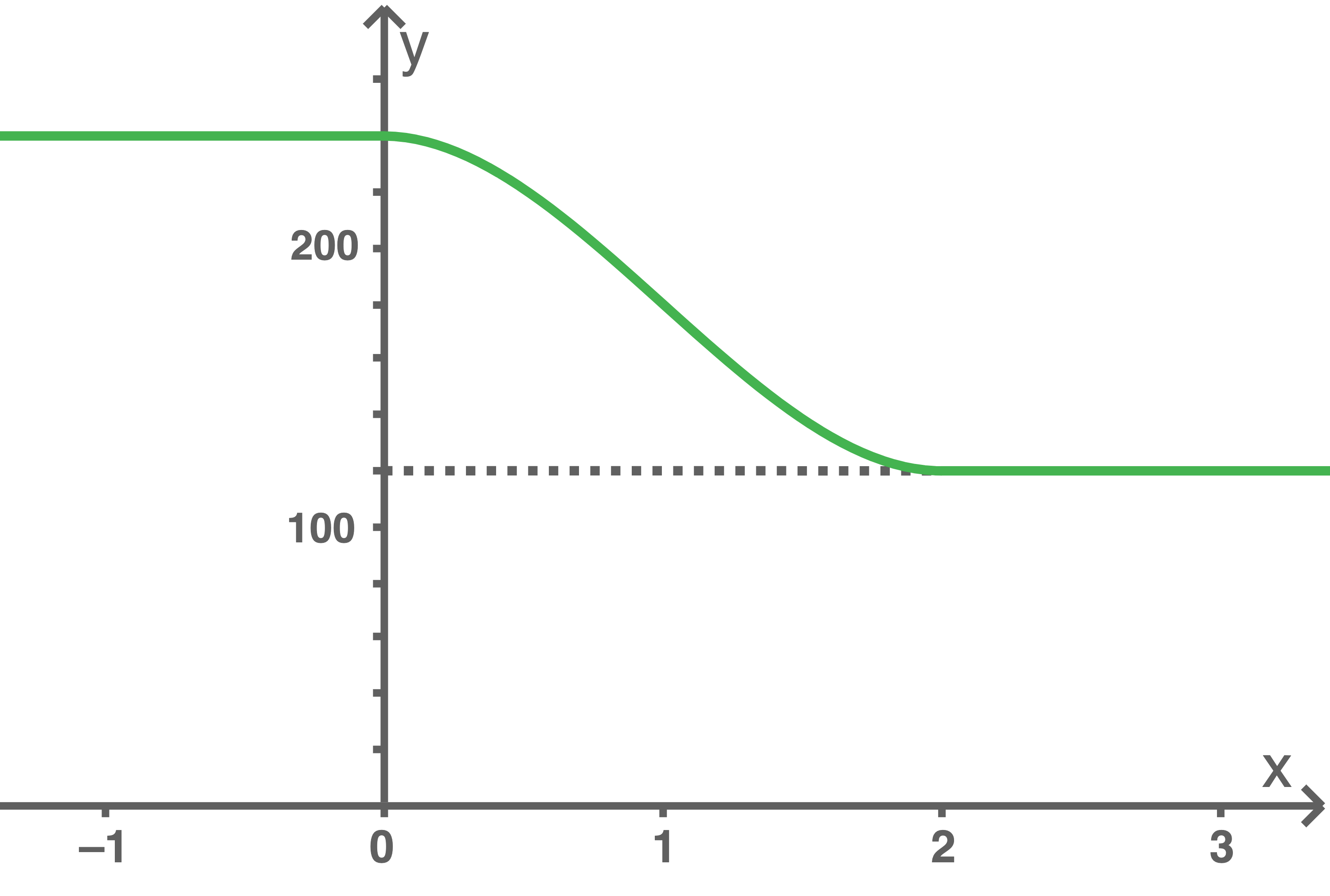
Abb. 1
a)
Bestimme die Geschwindigkeit, die der ICE eine halbe Minute nach 15:00 Uhr hat. Zeige, dass die Geschwindigkeit in der ersten halben Minute nach 15:00 Uhr um einen kleineren Betrag abnimmt als in der darauf folgenden halben Minute.
(4 BE)
b)
Bestimme die Länge des Zeitraums, in dem die Geschwindigkeit höchstens  aber mindestens
aber mindestens  Kilometer pro Stunde beträgt.
Kilometer pro Stunde beträgt.
(3 BE)
c)
Gib mögliche Werte  und
und  an, sodass gilt:
an, sodass gilt: 
Deute die Aussage im Sachzusammenhang.
im Sachzusammenhang.
Deute die Aussage
(3 BE)
d)
Ermittle den Zeitpunkt, zu dem die Geschwindigkeit am stärksten abnimmt.
(3 BE)
e)
Bestimme einen Zeitraum, der frühestens um 14:59 Uhr beginnt und spätestens um 15:03 Uhr endet, in dem der ICE eine Strecke mit einer Länge von genau  zurücklegt.
zurücklegt.
(5 BE)
f)
Untersuche, ob folgende Aussage richtig ist:
Wenn sich die Abnahme der Geschwindigkeit von 15:01 Uhr an nicht mehr verändern würde, dann käme der ICE von diesem Zeitpunkt an nach drei Kilometern zum Stehen.
Betrachtet wird die in Wenn sich die Abnahme der Geschwindigkeit von 15:01 Uhr an nicht mehr verändern würde, dann käme der ICE von diesem Zeitpunkt an nach drei Kilometern zum Stehen.
(6 BE)
g)
Bestimme die passenden Werte von 
 und
und 
[Zur Kontrolle:

 ]
]
[Zur Kontrolle:
(5 BE)
h)
Berechne den Wert des Terms  Beschreibe mithilfe der Abbildung 2, wie man zu diesem Wert mit geometrischen Überlegungen gelangen kann.
Beschreibe mithilfe der Abbildung 2, wie man zu diesem Wert mit geometrischen Überlegungen gelangen kann.
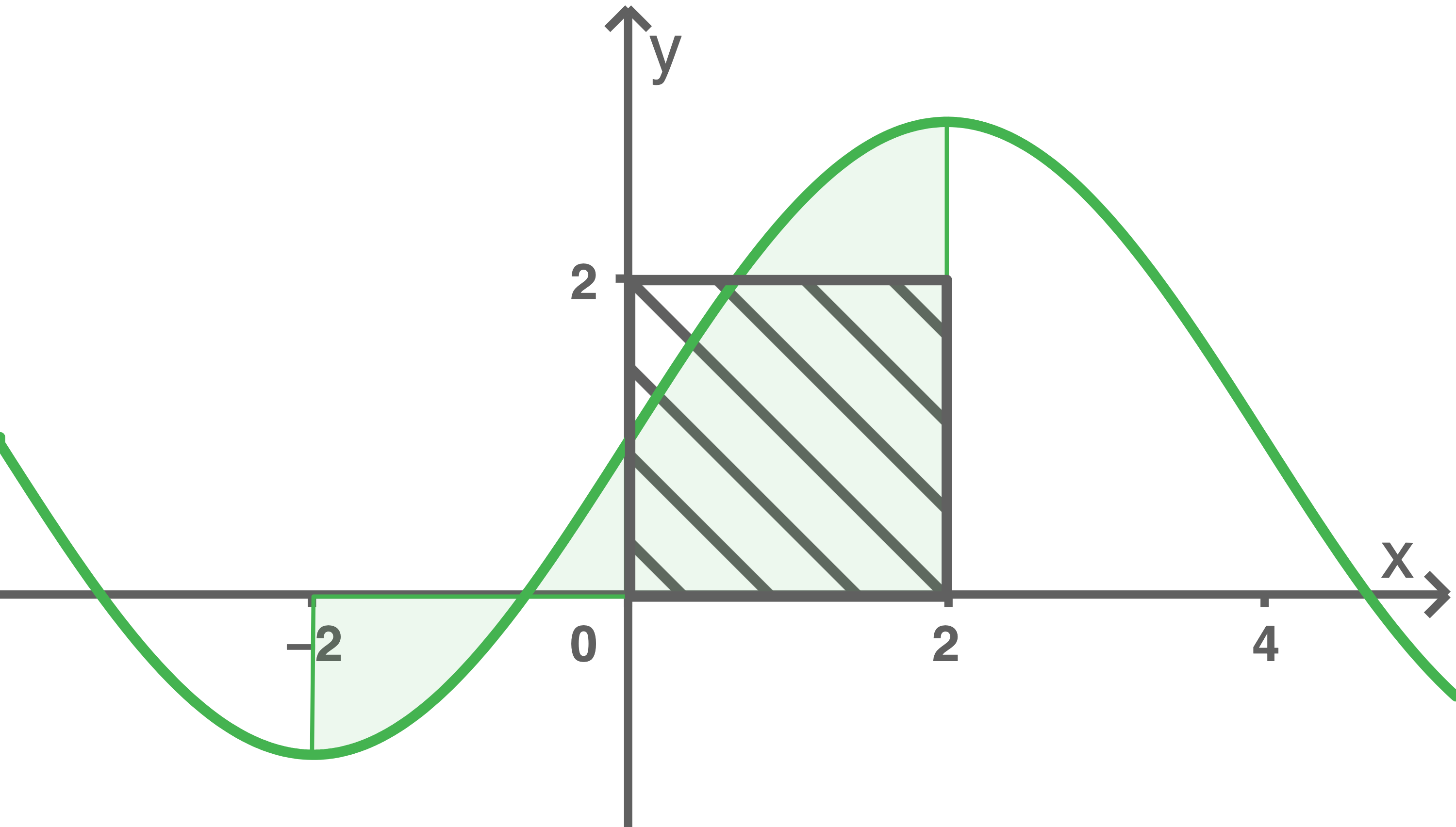
Die Punkte des Graphen von 
Abb. 2
(6 BE)
i)
Für jeden Wendepunkt des Graphen von  wird die Gerade betrachtet, die durch diesen Wendepunkt und den Punkt
wird die Gerade betrachtet, die durch diesen Wendepunkt und den Punkt  verläuft.
verläuft.
Untersuche, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den Graphen von ist.
ist.
Untersuche, ob eine dieser Geraden im jeweiligen Wendepunkt Tangente an den Graphen von
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Bestimmung der Geschwindigkeit

 Die Geschwindigkeit des ICE beträgt eine halbe Minute nach 15:00 ca.
Die Geschwindigkeit des ICE beträgt eine halbe Minute nach 15:00 ca.  Bestimmung der Geschwindigkeitsabnahme im ersten Intervall
Bestimmung der Geschwindigkeitsabnahme im ersten Intervall

 Bestimmung der Geschwindigkeitsabnahme im zweiten Intervall
Bestimmung der Geschwindigkeitsabnahme im zweiten Intervall

 Folglich ist die Geschwindigkeitabnahme im zweiten Intervall größer, als die im ersten Intervall.
Folglich ist die Geschwindigkeitabnahme im zweiten Intervall größer, als die im ersten Intervall.
b)
Da der Graph der Funktion  nach dem Schaubild streng monoton fällt, gibt es eine Stelle
nach dem Schaubild streng monoton fällt, gibt es eine Stelle  an der
an der  gilt und eine Stelle
gilt und eine Stelle  an der
an der  gilt. Das Intervall ist
gilt. Das Intervall ist ![\([x_1;x_2].\)](https://mathjax.schullv.de/b821d259d7ab297625b24070667f9e5b80296d41546f9b11b7625e2c708c41ad?color=5a5a5a) Berechnung von
Berechnung von  Es muss
Es muss  gelten.
Mit dem solve-Befehl des CAS ergibt sich
gelten.
Mit dem solve-Befehl des CAS ergibt sich  Berechnung von
Berechnung von  Es muss
Es muss  gelten.
Mit dem solve-Befehl des CAS ergibt sich sich
gelten.
Mit dem solve-Befehl des CAS ergibt sich sich  Berechnung der Intervalllänge
Berechnung der Intervalllänge
![\(\begin{array}[t]{rll}
x_2 - x_1&=& 1,347 - 0,774 \\[5pt]
x_2 - x_1&=& 0,573
\end{array}\)](https://mathjax.schullv.de/0c319d0bba59ab19e84175c7881dca46a2d50b3e4a4455bf2f6d6f4a4dfbd44e?color=5a5a5a) Folglich ist der Zeitraum in dem der ICE zwischen
Folglich ist der Zeitraum in dem der ICE zwischen  und
und  fährt
fährt  Minuten lang.
Minuten lang.
c)
Deutung der Aussage im Sachzusammenhang
Die Aussage  bedeutet, dass die momentane Änderungsrate der Geschwindigkeit zu den Zeitpunkten
bedeutet, dass die momentane Änderungsrate der Geschwindigkeit zu den Zeitpunkten  und
und  identisch ist.
Berechnung der 1. Ableitung
identisch ist.
Berechnung der 1. Ableitung
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/d7de5d4b187401aa9a57a4f8af63935d61f00a59de6d2158cbe8a413ac56f1d4?color=5a5a5a) Angabe eines möglichen Wertepaars
Graphisches Darstellen mit Taschenrechner und Ablesen eines Wertepaars ergibt u.a. das Wertepaar:
Angabe eines möglichen Wertepaars
Graphisches Darstellen mit Taschenrechner und Ablesen eines Wertepaars ergibt u.a. das Wertepaar:  und
und  .
.
d)
Bestimmen des Minimum mit dem Taschenrechner ergibt:  ist für
ist für  minimal. Folglich nimmt um genau 15:01 Uhr die Geschwindigkeit am stärksten ab.
minimal. Folglich nimmt um genau 15:01 Uhr die Geschwindigkeit am stärksten ab.
e)
Die zurückgelegte Strecke  entspricht dem Flächeninhalt der Fläche, die der Graph mit der
entspricht dem Flächeninhalt der Fläche, die der Graph mit der  -Achse einschließt. Bei der Strecke muss beachtet werden, dass die
-Achse einschließt. Bei der Strecke muss beachtet werden, dass die  -Achse in
-Achse in  angegeben ist und die
angegeben ist und die  -Achse in
-Achse in  angegeben ist. Bei Beginn eines solchen Zeitraums z.B. um 15:00 Uhr ergibt sich:
angegeben ist. Bei Beginn eines solchen Zeitraums z.B. um 15:00 Uhr ergibt sich:
![\(\begin{array}[t]{rll}
s&=& \dfrac{1}{60} \cdot \displaystyle\int_{0}^{2}f(x)\;\mathrm dx \\[5pt]
s&=& \dfrac{1}{60} \cdot \left[7,5x^4 - 30x^3+240 \right]_0^2 \\[5pt]
s&=& \dfrac{1}{60} \cdot \left( 7,5 \cdot 2^4 - 30 \cdot 2^3+240 \right) \\[5pt]
s&=& 6 \; [\text{km}]
\end{array}\)](https://mathjax.schullv.de/23b4eb2e4d6b4e8f584cdcabcc9490fc0c34a02d260141cda51a5456dbf36cc0?color=5a5a5a) Der Zug hat bis 15:02 Uhr
Der Zug hat bis 15:02 Uhr  zurückgelegt. Folglich muss noch der Zeitpunkt bestimmt werden, an dem der Zug einen weiteren Kilometer zurückgelegt hat.
zurückgelegt. Folglich muss noch der Zeitpunkt bestimmt werden, an dem der Zug einen weiteren Kilometer zurückgelegt hat.
![\(\begin{array}[t]{rll}
\dfrac{1}{60} \cdot f(2) \cdot t&=& 1 \\[5pt]
\dfrac{1}{60} \cdot 120 \cdot t&=& 1 \\[5pt]
2 \cdot t&=& 1 &\quad \scriptsize \mid\; :2 \\[5pt]
t&=& 0,5
\end{array}\)](https://mathjax.schullv.de/e8b3cafeb5a184155f75161cc2fae17c7857986e2ab7498fa75883c7bb4b8be2?color=5a5a5a) Somit endet der Zeitraum, der um 15:00 Uhr beginnt nach
Somit endet der Zeitraum, der um 15:00 Uhr beginnt nach  Minuten.
Minuten.
f)
Die Tangente des Graphen von  an der Stelle
an der Stelle  wird auf Nullstellen untersucht.
Aufstellen der Tangente
wird auf Nullstellen untersucht.
Aufstellen der Tangente
![\(\begin{array}[t]{rll}
y&=& f](https://mathjax.schullv.de/6bb20d1899d302b33da04856112dfba0552c658b3943d09f259e4aca009eb059?color=5a5a5a) Nullstelle der Tangente
Nullstelle der Tangente
![\(\begin{array}[t]{rll}
y&=& 0 \\[5pt]
-90 \cdot x+ 270 &=& 0 &\quad \scriptsize \mid\; -270 \\[5pt]
-90 \cdot x &=& -270 &\quad \scriptsize \mid\; :90 \\[5pt]
x &=& 3
\end{array}\)](https://mathjax.schullv.de/193a4c318a9493d82911f2cc3112ac8247bb35eb05abcf0ac4bb2247af2642ce?color=5a5a5a) Zurückgelegte Strecke
Die zurückgelegte Strecke
Zurückgelegte Strecke
Die zurückgelegte Strecke  entspricht dem Flächeninhalt der Fläche, die der Graph von
entspricht dem Flächeninhalt der Fläche, die der Graph von  mit der
mit der  -Achse im Intervall
-Achse im Intervall ![\([1;3]\)](https://mathjax.schullv.de/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c?color=5a5a5a) einschließt. Bei der Strecke muss beachtet werden, dass die
einschließt. Bei der Strecke muss beachtet werden, dass die  -Achse in
-Achse in  angegeben ist und die
angegeben ist und die  -Achse in
-Achse in  angegeben ist.
angegeben ist.
![\(\begin{array}[t]{rll}
s&=& \dfrac{1}{60} \cdot \dfrac{1}{2} \cdot 2 \cdot f(1)\\[5pt]
s&=& \dfrac{1}{60} \cdot 180 \\[5pt]
s&=& 3 \; [\text{km}]
\end{array}\)](https://mathjax.schullv.de/874ad4955b07e4e6dfd5b94a4d5360f2bdb9ab3d7a85f03680447a2974a6e999?color=5a5a5a) Die Aussage ist richtig.
Die Aussage ist richtig.
g)
Berechung von a
Der Parameter  gibt die Streckung entlang der
gibt die Streckung entlang der  -Achse an. Dieser ergibt sich aus der halbierten Differenz der
-Achse an. Dieser ergibt sich aus der halbierten Differenz der  -Werte der beiden aufeinanderfolgenden Extrempunkte.
-Werte der beiden aufeinanderfolgenden Extrempunkte.
![\(\begin{array}[t]{rll}
a &=& \dfrac{1}{2} \cdot (3 - (-1)) \\[5pt]
a &=& 2
\end{array}\)](https://mathjax.schullv.de/26980a64f0bf42f039f0966b85c4308167dc8c0ed9f6f3d20cbb59d45178f9c3?color=5a5a5a) Berechung von b
Der Parameter
Berechung von b
Der Parameter  gibt die Streckung entlang der x-Achse an.
gibt die Streckung entlang der x-Achse an.
![\(\begin{array}[t]{rll}
b &=& \dfrac{\pi}{2-(-2)} \\[5pt]
b &=& \dfrac{\pi}{4} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7430fd4bdae2ea2e16769d7e32379b6a1be3db22952b3dd8093e7a9e9eacc338?color=5a5a5a) Berechung von c
Der Parameter
Berechung von c
Der Parameter  gibt die Verschiebung entlang der
gibt die Verschiebung entlang der  -Achse an. Dieser ergibt sich aus dem Mittelwert der
-Achse an. Dieser ergibt sich aus dem Mittelwert der  -Werte der beiden aufeinanderfolgenden Extrempunkte.
-Werte der beiden aufeinanderfolgenden Extrempunkte.
![\(\begin{array}[t]{rll}
c &=& \dfrac{1}{2} \cdot (3 + (-1)) \\[5pt]
c &=& 1
\end{array}\)](https://mathjax.schullv.de/faead8130fe7d18d512dc4debe6af29009436ced972c82789b39ff5e06a11e17?color=5a5a5a)
h)
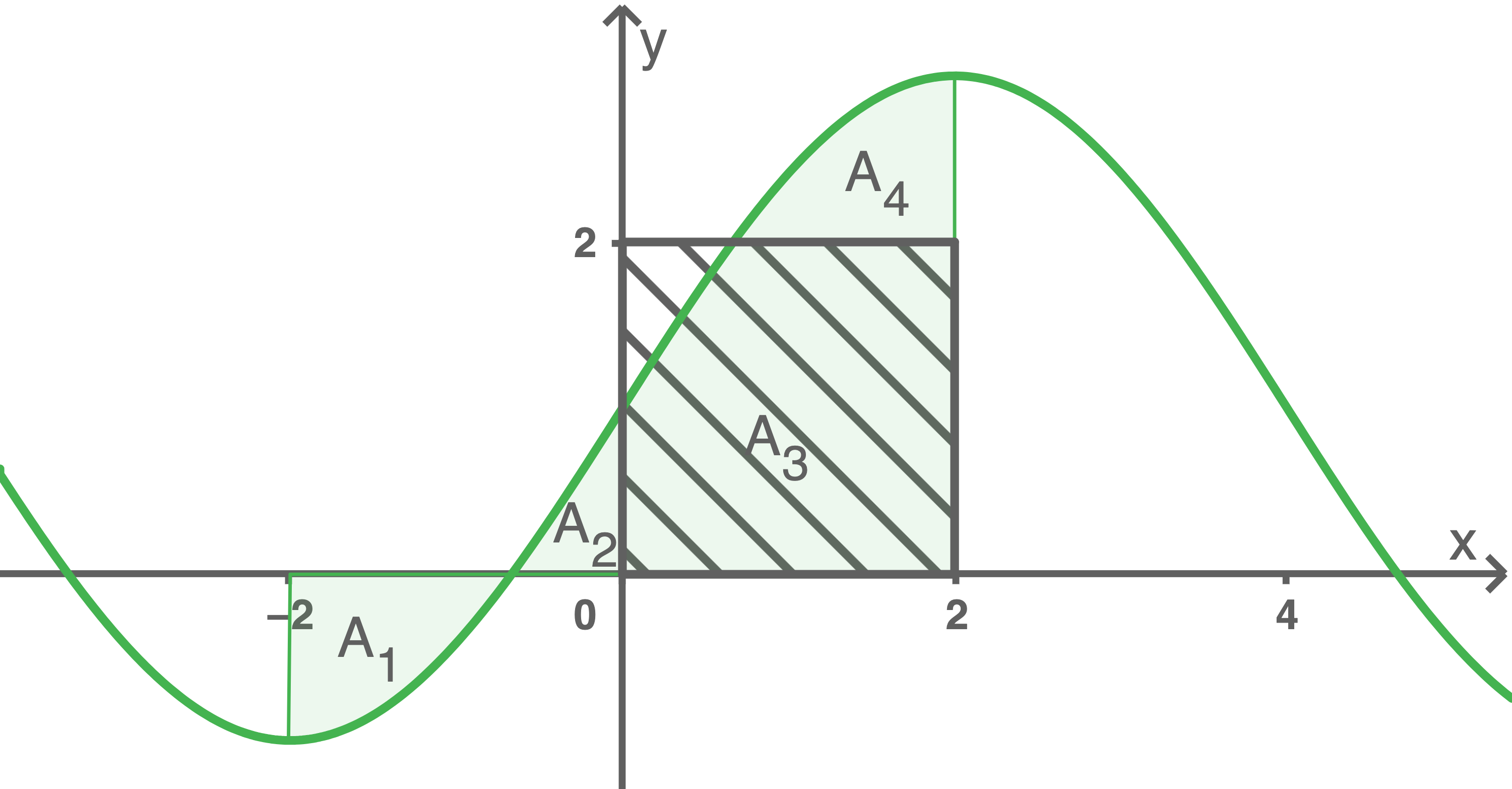
i)
Koordinaten der Wendepunkte
Der Aufgabenstellung kann entnommen werden, dass die Wendepunkte die Koordinaten  mit
mit  besitzen.
Steigung der Geraden
Die betrachteten Geraden haben folgende Steigung:
besitzen.
Steigung der Geraden
Die betrachteten Geraden haben folgende Steigung:
![\(\begin{array}[t]{rll}
m &=& \dfrac{\Delta y}{\Delta x}\\[5pt]
m &=& \dfrac{2022 - 1}{2022-4k} \\[5pt]
m &=& \dfrac{2021}{2022-4k} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e61da629c916414d98b01f8ed78b588a16d71bd6d436ec7db5dfeee4ea739489?color=5a5a5a) Folglich ist die Steigung für jedes
Folglich ist die Steigung für jedes  rational. Die Steigung in den Wendestellen ist nach Aufgabenstellung
rational. Die Steigung in den Wendestellen ist nach Aufgabenstellung  und somit irrational. Folgich ist keine der Geraden eine Tangente einer Wendestelle.
und somit irrational. Folgich ist keine der Geraden eine Tangente einer Wendestelle.