1 Analysis – Pflichtaufgabe
Gegeben ist die in  definierte Funktion
definierte Funktion  Die Abbildung 1 zeigt den Graphen
Die Abbildung 1 zeigt den Graphen  von
von 
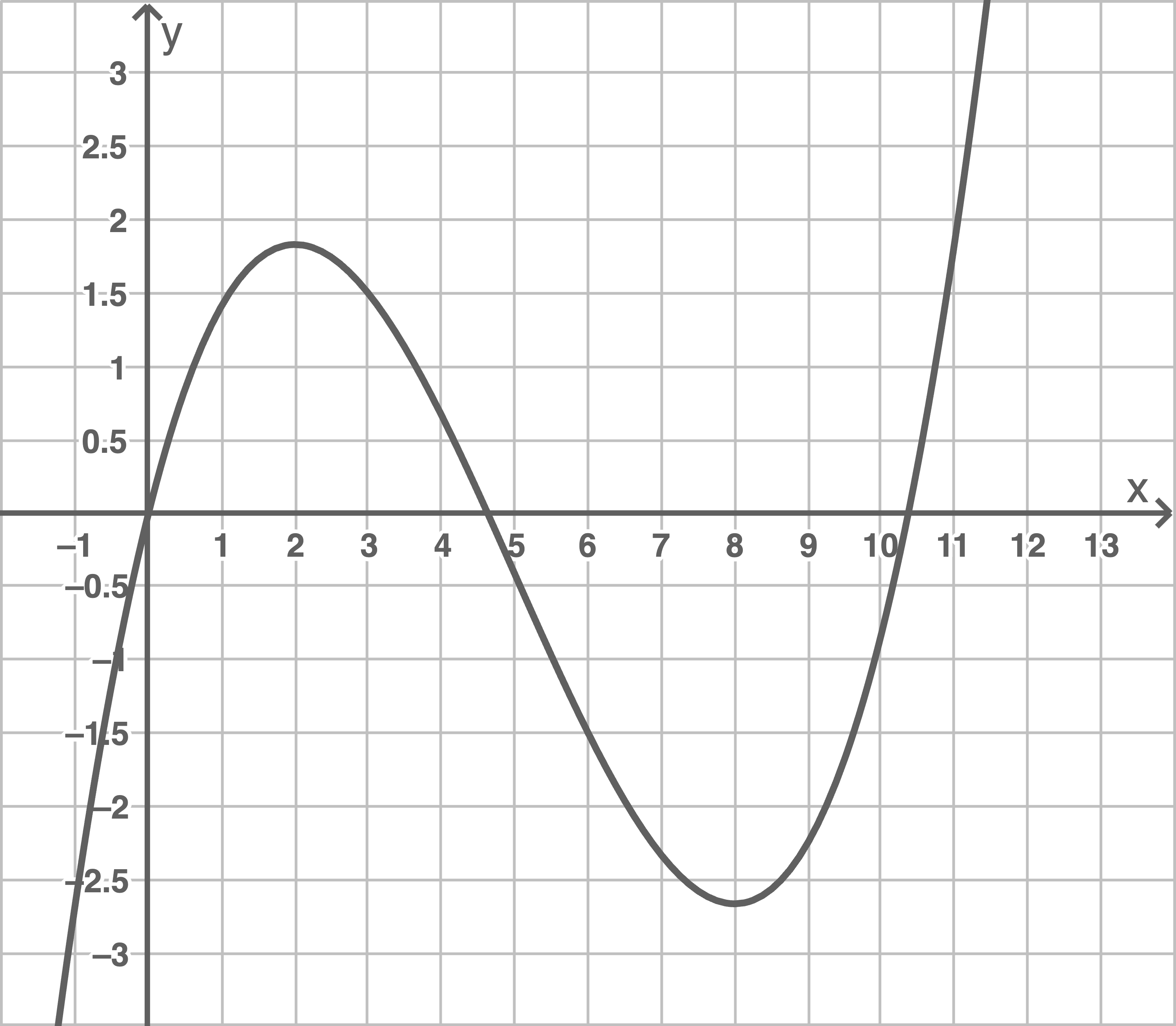
Abbildung 1
1.1
(5 BE)
1.2
Die Tangente  schließt mit den Koordinatenachsen ein Dreieck ein. Dieses Dreieck rotiert um die
schließt mit den Koordinatenachsen ein Dreieck ein. Dieses Dreieck rotiert um die  -Achse.
Ermittle das Volumen des entstehenden Rotationskörpers.
-Achse.
Ermittle das Volumen des entstehenden Rotationskörpers.
(4 BE)
1.3
Betrachtet wird die Funktion  mit der Gleichung
mit der Gleichung  Bestimme ohne Rechnung die Anzahl der Lösungen der Gleichung
Bestimme ohne Rechnung die Anzahl der Lösungen der Gleichung 
(5 BE)
1.4
Die Funktion  gehört zur Funktionenschar
gehört zur Funktionenschar  mit der Gleichung
mit der Gleichung  und
und  Die Graphen von
Die Graphen von  heißen
heißen 
In einem Freizeitpark wird zu jedem Zeitpunkt an den Ein- und Ausgängen erfasst, wie viele Besucher in den Park gehen oder den Park verlassen.
Die Funktion
1.4.1
Alle Graphen  schneiden die
schneiden die  -Achse im Koordinatenursprung.
Zeige, dass dort die Schnittwinkel aller Graphen mit der
-Achse im Koordinatenursprung.
Zeige, dass dort die Schnittwinkel aller Graphen mit der  -Achse gleich groß sind.
-Achse gleich groß sind.
(2 BE)
1.4.2
Es gibt Werte von  für die
für die  die beiden Extremstellen
die beiden Extremstellen  und
und  hat.
Ermittle die Werte von
hat.
Ermittle die Werte von  für die der Abstand zwischen
für die der Abstand zwischen  und
und  genau 8 beträgt.
genau 8 beträgt.
(5 BE)
1.5
Übersteigt die momentane Änderungsrate der Besucherzahl den Wert von 1500 Personen pro Stunde, wird zusätzliches Personal für die Abfertigung an den Kassen bereitgestellt.
Gib mit Hilfe der Abbildung 1 diesen Zeitraum an.
(2 BE)
1.6
Gib mit Hilfe der Abbildung 1 den Zeitpunkt an, zu dem die Anzahl der Besucher am größten ist. Begründe deine Angabe.
(2 BE)
1.7
Berechne den Wert des Terms  und deute das Ergebnis im Sachzusammenhang.
und deute das Ergebnis im Sachzusammenhang.
(4 BE)
1.8
Für den Freizeitpark soll ein Teilstück einer Achterbahn neu konstruiert werden. Beginn und Ende dieses Streckenverlaufs sind horizontal.
Im Modell kann die Profillinie dieses Teilstücks zwischen den Punkten  und
und  durch den Graphen der Funktion
durch den Graphen der Funktion  mit
mit  beschrieben werden (siehe Abbildung 2).
Eine Längeneinheit im Koordinatensystem entspricht
beschrieben werden (siehe Abbildung 2).
Eine Längeneinheit im Koordinatensystem entspricht  in der Realität.
in der Realität.
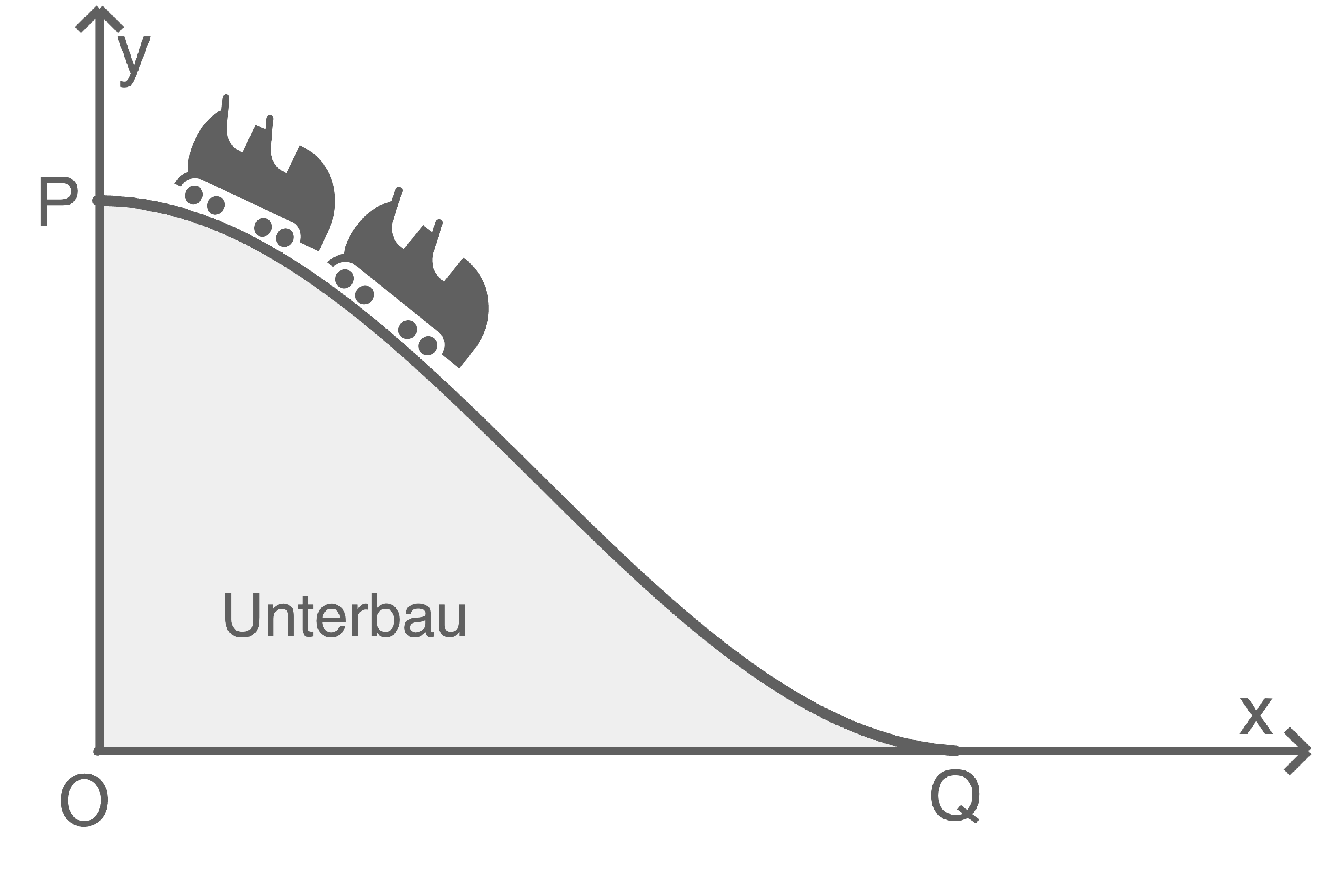
Abbildung 2
1.8.1
Gib die Koordinaten von  an.
an.
(1 BE)
1.8.2
Der Unterbau der Achterbahn soll mit Lichternetzen behängt werden. Dazu wird der Inhalt der gefärbten Querschnittsfläche (siehe Abbildung 2) berechnet.
Begründe, dass dieser Flächeninhalt mit Hilfe des Terms  berechnet werden kann.
berechnet werden kann.
(4 BE)
1.8.3
Aus Sicherheitsgründen darf der Betrag des Neigungswinkels der Bahnkurve gegenüber der Horizontalen an keiner Stelle größer als  sein.
Berechne den Wert von
sein.
Berechne den Wert von  so, dass unter Einhaltung dieser Bedingung die Länge der Strecke
so, dass unter Einhaltung dieser Bedingung die Länge der Strecke  minimal wird.
minimal wird.
(6 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Koordinaten berechnen
Ableitungen bestimmen:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/5fda7a03b5a328fe4943ab49dface2bd5781871556f8d332c80ae7cb1db65275?color=5a5a5a) Notwendige Bedingung für Wendestellen anwenden:
Notwendige Bedingung für Wendestellen anwenden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/00d8f2145fc412c7b0514dd42719efa0c2b9127be8824d35d14188d28d149a6e?color=5a5a5a) Da vorausgesetzt ist, dass es genau einen Wendepunkt
Da vorausgesetzt ist, dass es genau einen Wendepunkt  gibt, kann auf das Überprüfen der hinreichenden Bedingung verzichtet werden.
gibt, kann auf das Überprüfen der hinreichenden Bedingung verzichtet werden.
 -Koordinate bestimmen:
-Koordinate bestimmen:
![\(\begin{array}[t]{rll}
f(5)&=& \dfrac{1}{24} \cdot 5^3-\dfrac{5}{8} \cdot 5^2+2 \cdot 5 &\\[5pt]
&=& -\dfrac{5}{12}
\end{array}\)](https://mathjax.schullv.de/0f8a2af98806b38efa1e8d43067dd2cf4415bfa07640ac6b1066bb3d1322ed6c?color=5a5a5a) Der Wendepunkt hat die Koordinaten
Der Wendepunkt hat die Koordinaten  Tangentengleichung bestimmen
Für die Steigung am Wendepunkt gilt:
Tangentengleichung bestimmen
Für die Steigung am Wendepunkt gilt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/1ede389cd22a2dd65f030605987bab8cbb077960de4d8fa2784180ab3f1f9e4c?color=5a5a5a) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  sowie der Steigung
sowie der Steigung  in die allgemeine Tangentengleichung liefert:
in die allgemeine Tangentengleichung liefert:
![\(\begin{array}[t]{rll}
t: \quad \quad y&=&m\cdot x+c & \\[5pt]
-\dfrac{5}{12}&=& -\dfrac{9}{8} \cdot 5+c &\quad \scriptsize \mid\; +\dfrac{45}{8} \\[5pt]
\dfrac{125}{24}&=& c
\end{array}\)](https://mathjax.schullv.de/bfb7b9a5372d63a8c4acd8dd89c4664bf248a2f74323b5a1c8fdb2c9ab640da6?color=5a5a5a) Die Gleichung der Tangente
Die Gleichung der Tangente  ist somit gegeben durch:
ist somit gegeben durch:

1.2
1. Schritt: Nullstelle berechnen
Der Schnittpunkt der Tangente  mit der
mit der  -Achse ergibt sich mit dem
-Achse ergibt sich mit dem  -Achsenabschnitt direkt zu
-Achsenabschnitt direkt zu  Für die Schnittstelle mit der
Für die Schnittstelle mit der  -Achse gilt:
-Achse gilt:
![\(\begin{array}[t]{rll}
0&=& -\dfrac{9}{8} \cdot x+\dfrac{125}{24} &\quad \scriptsize \,\bigg \vert \, \; +\dfrac{9}{8} \cdot x \\[5pt]
\dfrac{9}{8} \cdot x&=& \dfrac{125}{24} &\quad \scriptsize \,\bigg \vert \, \; \cdot \dfrac{8}{9} \\[5pt]
x&=& \dfrac{125}{27}
\end{array}\)](https://mathjax.schullv.de/dc75235fdcd26e9ecf3da9f4f46bb06a976f464c4e7d20671bba57d43c1f3c2e?color=5a5a5a) 2. Schritt: Volumen ermitteln
Rotiert ein Dreieck um eine Achse, so entsteht ein Kegel.
Mit dem Radius
2. Schritt: Volumen ermitteln
Rotiert ein Dreieck um eine Achse, so entsteht ein Kegel.
Mit dem Radius  und der Höhe
und der Höhe  des Kegels ergibt sich das Volumen des Rotationskörpers somit zu:
des Kegels ergibt sich das Volumen des Rotationskörpers somit zu:
![\(\begin{array}[t]{rll}
V_{\text{Kegel}}&=& \dfrac{1}{3}\cdot \pi \cdot r^2 \cdot h & \\[5pt]
&=& \dfrac{1}{3}\cdot \pi \cdot \left(\dfrac{125}{24}\right)^2 \cdot \dfrac{125}{27} & \\[5pt]
&\approx& 131,5 \; \text{VE}
\end{array}\)](https://mathjax.schullv.de/62cdf4dd28ffc3ee76dd815dfdcb60e9b3d3aa408d3061e8a854619cc932bc38?color=5a5a5a)
1.3
Die Funktion  beschreibt den Inhalt der Fläche, die der Graph von
beschreibt den Inhalt der Fläche, die der Graph von  mit der
mit der  -Achse einschließt.
Aus der Abbildung in der Aufgabenstellung kann abgelesen werden, dass die Stammfunktion
-Achse einschließt.
Aus der Abbildung in der Aufgabenstellung kann abgelesen werden, dass die Stammfunktion  von
von  die
die  -Achse im Koordinatenursprung schneidet und dort einen Tiefpunkt besitzt.
Da der Inhalt des oberhalb der
-Achse im Koordinatenursprung schneidet und dort einen Tiefpunkt besitzt.
Da der Inhalt des oberhalb der  -Achse liegenden Flächenstücks kleiner als der Inhalt des unterhalb der
-Achse liegenden Flächenstücks kleiner als der Inhalt des unterhalb der  -Achse liegenden Flächenstücks ist, muss der Graph von
-Achse liegenden Flächenstücks ist, muss der Graph von  einen weiteren Tiefpunkt, der unterhalb der
einen weiteren Tiefpunkt, der unterhalb der  -Achse liegt, besitzen.
Folglich hat
-Achse liegt, besitzen.
Folglich hat  neben
neben  zwei weitere Nullstellen.
Die Gleichung
zwei weitere Nullstellen.
Die Gleichung  hat also 3 Lösungen.
hat also 3 Lösungen.
1.4.1
Die Schnittwinkel aller Graphen mit der  -Achse im Koordinatenursprung sind genau dann gleich groß, wenn die Graphen in diesem Punkt die gleiche Steigung haben.
Ableitung bestimmen:
-Achse im Koordinatenursprung sind genau dann gleich groß, wenn die Graphen in diesem Punkt die gleiche Steigung haben.
Ableitung bestimmen:
 Im Ursprung gilt also:
Im Ursprung gilt also:
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/82a760f1057e1fe2546e3409005ada97a462a7b230772498a6a3b1eb03955eff?color=5a5a5a) Die Steigung der Graphen im Koordinatenursprung ist somit unabhängig von
Die Steigung der Graphen im Koordinatenursprung ist somit unabhängig von  Damit sind auch die Schnittwinkel alle gleich groß.
Damit sind auch die Schnittwinkel alle gleich groß.
1.4.2
1. Schritt: Extremstellen bestimmen
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/56b5ceecd79837d92b6fe798db418d55b11f55fd1be32d5e3717838068102135?color=5a5a5a) Mit der
Mit der  -Formel folgt:
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1;2}&=& -\dfrac{(-16a)}{2} \pm \sqrt{\left(\dfrac{(-16a)}{2}\right)^2-16} \\[5pt]
&=& 8a\pm\sqrt{64a^2-16} & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/461b66f8f70ad7eb3f43e43845278d424b37119f84c9537225c78861f521a7e8?color=5a5a5a) Da vorausgesetzt ist, dass es Werte von
Da vorausgesetzt ist, dass es Werte von  gibt, für die
gibt, für die  genau zwei Extremstellen besitzt, kann auf das Überprüfen der hinreichenden Bedingung verzichtet werden.
2. Schritt: Wert von
genau zwei Extremstellen besitzt, kann auf das Überprüfen der hinreichenden Bedingung verzichtet werden.
2. Schritt: Wert von  berechnen
Die Extremstellen
berechnen
Die Extremstellen  und
und  haben genau den Abstand
haben genau den Abstand  zueinander.
Es soll nun gelten:
zueinander.
Es soll nun gelten:
![\(\begin{array}[t]{rll}
2\cdot \sqrt{64a^2-16}&=& 8 &\quad \scriptsize \mid\;:2 \\[5pt]
\sqrt{64a^2-16}&=& 4 &\quad \scriptsize \mid\;(\,)^2 \\[5pt]
64a^2-16&=& 16 &\quad \scriptsize \mid\; +16 \\[5pt]
64a^2&=& 32 &\quad \scriptsize \mid\; :64 \\[5pt]
a^2&=& 0,5 &\quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
a&=& \pm\dfrac{1}{2}\sqrt{2}
\end{array}\)](https://mathjax.schullv.de/6de9077bda0c408dc5877d54d5dc7256a2e29304e4059aeb2c0779b6299f7f3a?color=5a5a5a) Für die Werte
Für die Werte  beträgt der Abstand zwischen
beträgt der Abstand zwischen  und
und  somit genau 8.
somit genau 8.
1.5
Mehr als 1500 Besucher entspricht Funktionswerten mit  Damit ergibt sich graphisch der Zeitraum von ca. 11:10 Uhr bis 13:00 Uhr
Damit ergibt sich graphisch der Zeitraum von ca. 11:10 Uhr bis 13:00 Uhr
1.6
Die Nullstelle von  die das oberhalb der
die das oberhalb der  -Achse liegende Flächenstück rechts begrenzt, ist etwa an der Stelle
-Achse liegende Flächenstück rechts begrenzt, ist etwa an der Stelle  Ab diesem Zeitpunkt nimmt die Besucheranzahl wieder ab. Die Anzahl der Besucher ist somit gegen 14:40 Uhr am größten.
Alternative Begründung:
Die Nullstellen von
Ab diesem Zeitpunkt nimmt die Besucheranzahl wieder ab. Die Anzahl der Besucher ist somit gegen 14:40 Uhr am größten.
Alternative Begründung:
Die Nullstellen von  sind Extremstellen der Stammfunktion
sind Extremstellen der Stammfunktion  welche die Anzahl der Besucher in Abhängigkeit von der Zeit modelliert. Da an der Nullstelle bei
welche die Anzahl der Besucher in Abhängigkeit von der Zeit modelliert. Da an der Nullstelle bei  von
von  ein Vorzeichenwechsel von
ein Vorzeichenwechsel von  nach
nach  vorliegt, liegt an dieser Stelle ein lokales Maximum vor. Damit ist die Besucherzahl gegen 14:40 Uhr am größten.
vorliegt, liegt an dieser Stelle ein lokales Maximum vor. Damit ist die Besucherzahl gegen 14:40 Uhr am größten.
1.7
Wert berechnen
Ergebnis deuten
Um 18 Uhr befinden sich keine Besucher mehr im Park.
1.8.1
Da der Punkt  auf der
auf der  -Achse liegt, folgt:
-Achse liegt, folgt:
![\(\begin{array}[t]{rll}
h(0)&=& 25 \cdot \cos (b \cdot 0)+25 &\\[5pt]
&=& 25\cdot 1+25 &\\[5pt]
&=& 50
\end{array}\)](https://mathjax.schullv.de/589055d86d987dfe2caf5a9279231be2b56435cf247b352152bb5d76b0ef5c84?color=5a5a5a) Die Koordinaten von
Die Koordinaten von  sind somit gegeben durch
sind somit gegeben durch 
1.8.2
Der Graph von  ist punktsymmetrisch bezüglich des in der Abbildung liegenden Wendepunktes. Damit entspricht der Inhalt der Fläche zwischen dem Graphen von
ist punktsymmetrisch bezüglich des in der Abbildung liegenden Wendepunktes. Damit entspricht der Inhalt der Fläche zwischen dem Graphen von  und der
und der  -Achse dem Inhalt der Dreiecksfläche mit den Katheten
-Achse dem Inhalt der Dreiecksfläche mit den Katheten  und
und 
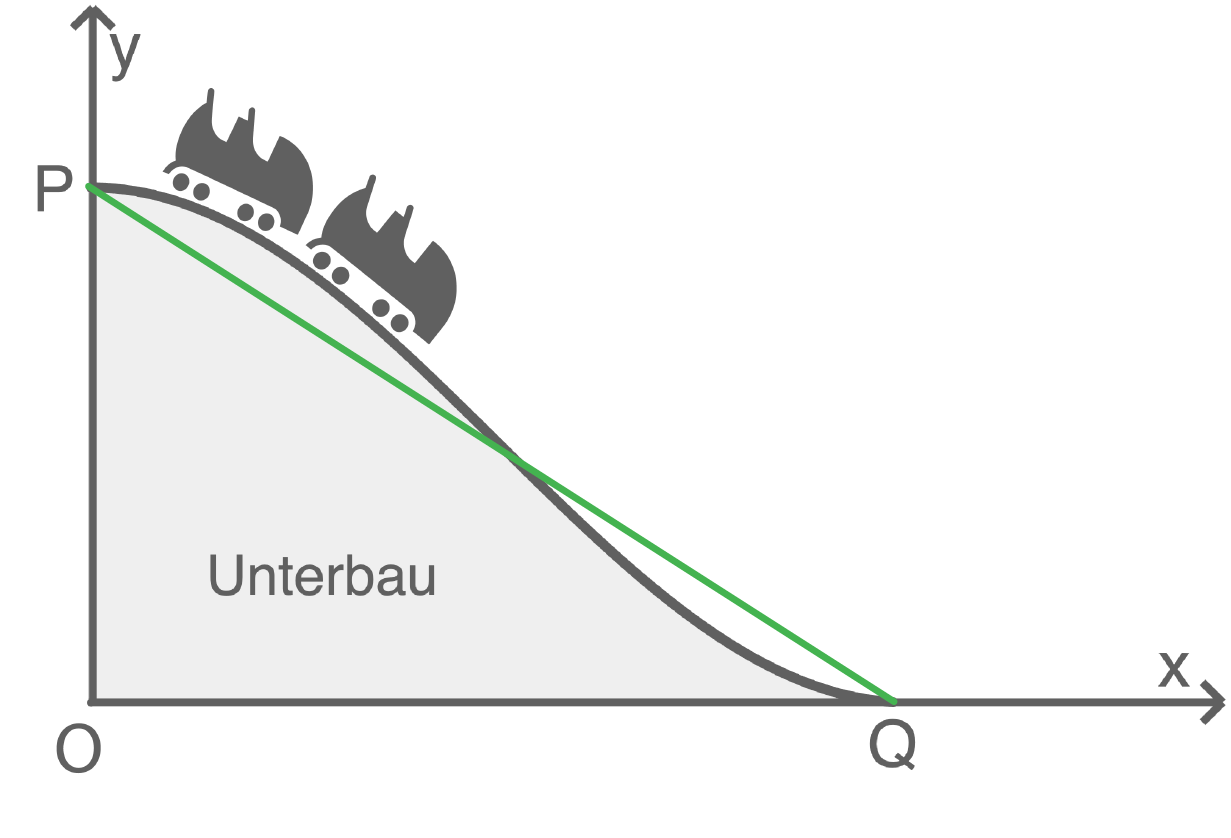
Hilfsskizze
1.8.3
Die Länge  der Strecke
der Strecke  ist minimal, wenn der Graph von
ist minimal, wenn der Graph von  im Wendepunkt bei
im Wendepunkt bei  den Anstiegswinkel
den Anstiegswinkel  hat.
Die abgebildete Teilstrecke
hat.
Die abgebildete Teilstrecke  in der Abbildung stellt eine halbe Periodenlänge dar. Für eine Periode
in der Abbildung stellt eine halbe Periodenlänge dar. Für eine Periode  von
von  gilt also
gilt also  Für den Faktor
Für den Faktor  der die Periodenlänge beeinflusst, gilt also:
der die Periodenlänge beeinflusst, gilt also:
 Einsetzen in
Einsetzen in  liefert nun:
liefert nun:
 Ableitung bestimmen:
Ableitung bestimmen:
 An der Wendestelle
An der Wendestelle  gilt somit:
gilt somit:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/2067c31040a80713649fbef9b6befa932dd7328643ec4f389251dbeb9ba34bd2?color=5a5a5a) Ein Neigungswinkel von
Ein Neigungswinkel von  bedeutet für die Steigung an der betrachteten Stelle:
bedeutet für die Steigung an der betrachteten Stelle:
 Es soll also gelten:
Es soll also gelten:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/62c2c6b119c2ef3ee1eaafb99bf412d526d26e62fb67d96d8201494db2530a34?color=5a5a5a) Der Wert von
Der Wert von  folgt nun mit:
folgt nun mit:
