Aufgabe B0

Analysis

Gegeben ist die Funktion $f$ mit der Gleichung

$f(x)=\dfrac{1}{x^2}$ mit $x \in\mathbb{R}$ , $x\neq0.$

Der Graph heißt $G$ . Die Tangente an $G$ im Punkt $P(1\mid f(1))$ heißt $t$ , die Normale im selben Punkt heißt $s.$

1.1

Ermittle die Gleichung von $t$ .

(3 BE)

1.2

Begründe ohne weitere Rechnung, dass das Dreieck, welches durch $t$ , $s$ und die $x$ -Achse gebildet wird, nicht gleichseitig ist.

(2 BE)

Die Schuppen einer bestimmten Reptilienart sind $6\,\text{mm}$ breit und $9\,\text{mm}$ lang. Eine solche Schuppe ist maßstabsgetreu abgebildet.

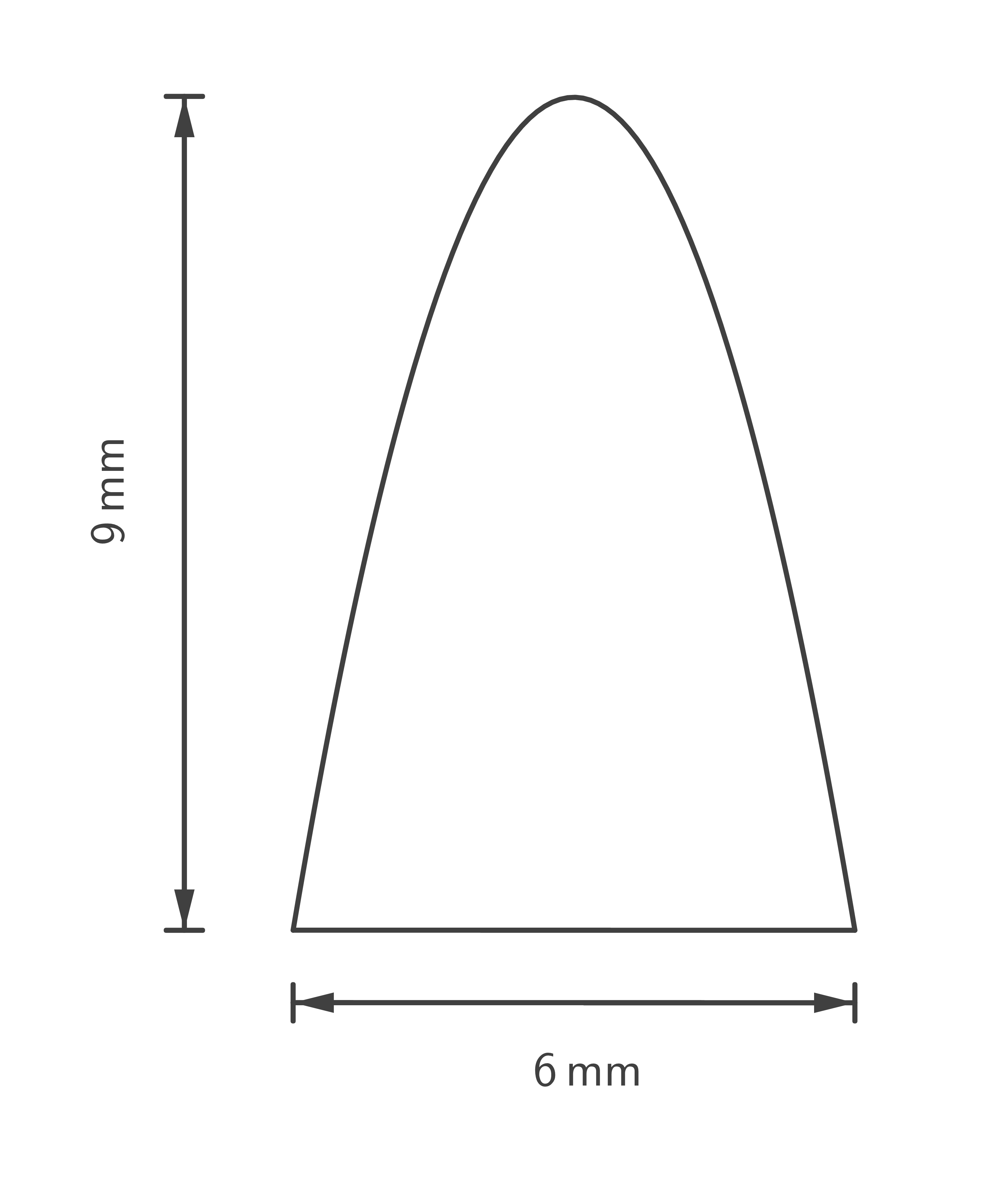
Schematische Darstellung einer Form mit den Maßen 9 mm Höhe und 6 mm Breite.

2.1

Ermittle eine mögliche Funktionsgleichung für die Beschreibung des gekrümmten Schuppenrandes.

(2 BE)

2.2

Schätze begründet ab, wie viele Schuppen einen $18\;000\,\text{mm}^2$ großen Hautbereich dieser Reptilienart vollständig bedecken würden.

(3 BE)

Analytische Geometrie

In einem Koordinatensystem werden die geraden Pyramiden $AB_tC_tD_tS_t$ mit $A(0\mid 0\mid 0),$ $B_t(t\mid 0\mid 0),$ $C_t(t\mid t\mid 0)$ und $D_t(0\mid t\mid 0)$ und $t\in\mathbb{R^+}$ betrachtet; die Punkte $S_t$ haben jeweils die $z$ -Koordinate $\dfrac{t}{8}.$
Die Abbildung zeigt die Pyramide für $t=6$ .

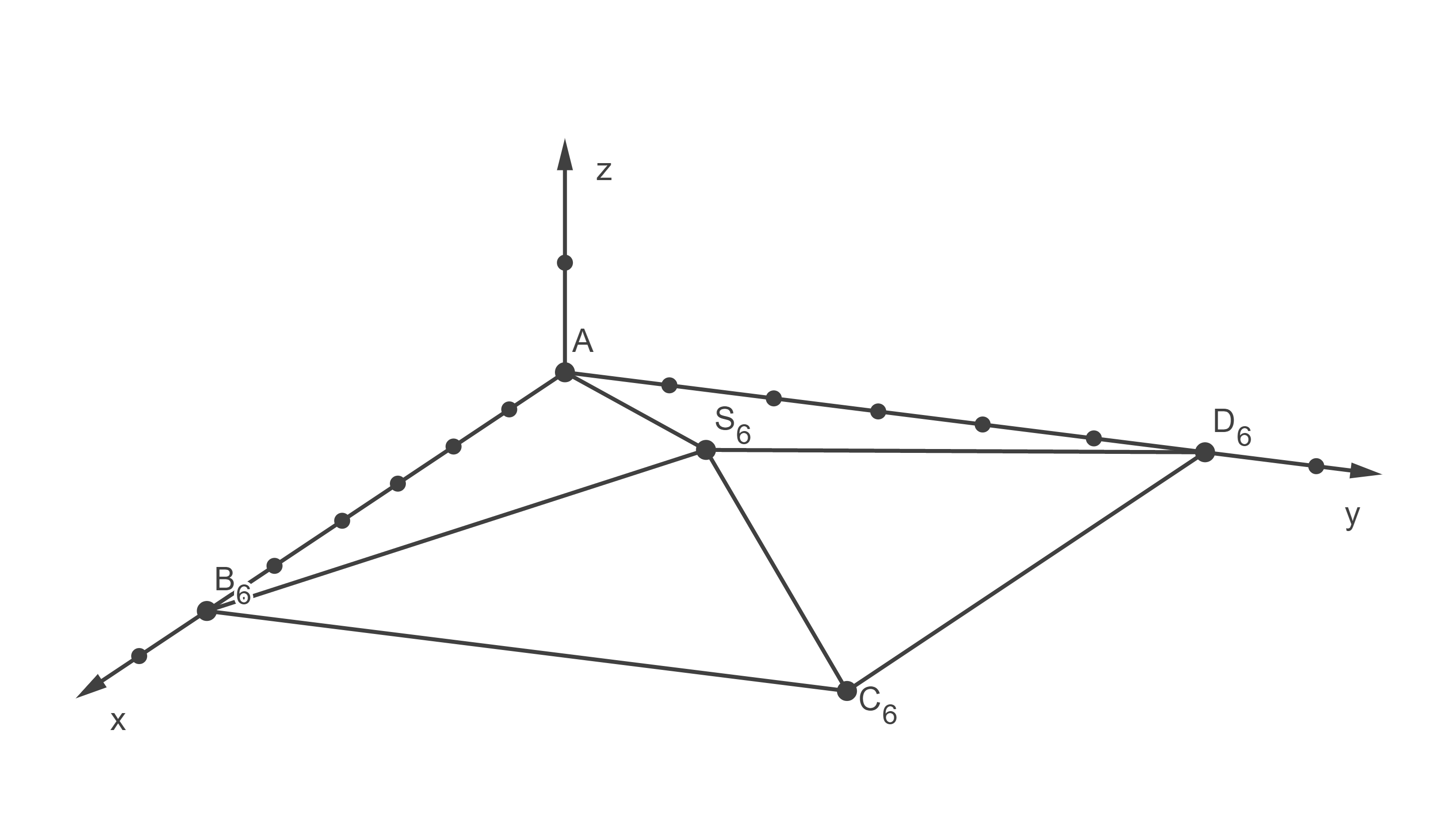Diagramm eines 3D-Koordinatensystems mit Punkten und Linien, die verschiedene Positionen darstellen.

Die Ebene $E:\,3y+4z=24$ enthält den Punkt $S_t$ für $t=12$ .

3.1

Begründe, dass $E$ parallel zur $x$ -Achse verläuft.

(1 BE)

3.2

Untersuche, für welche Werte von $t$ die Pyramide und die Ebene $E$ gemeinsame Punkte haben.

(4 BE)

Stochastik

4.1

Eine Zufallsgröße $X$ kann die Werte von $k=1$ bis $k=5$ annehmen mit $k \in\mathbb{N}$ .
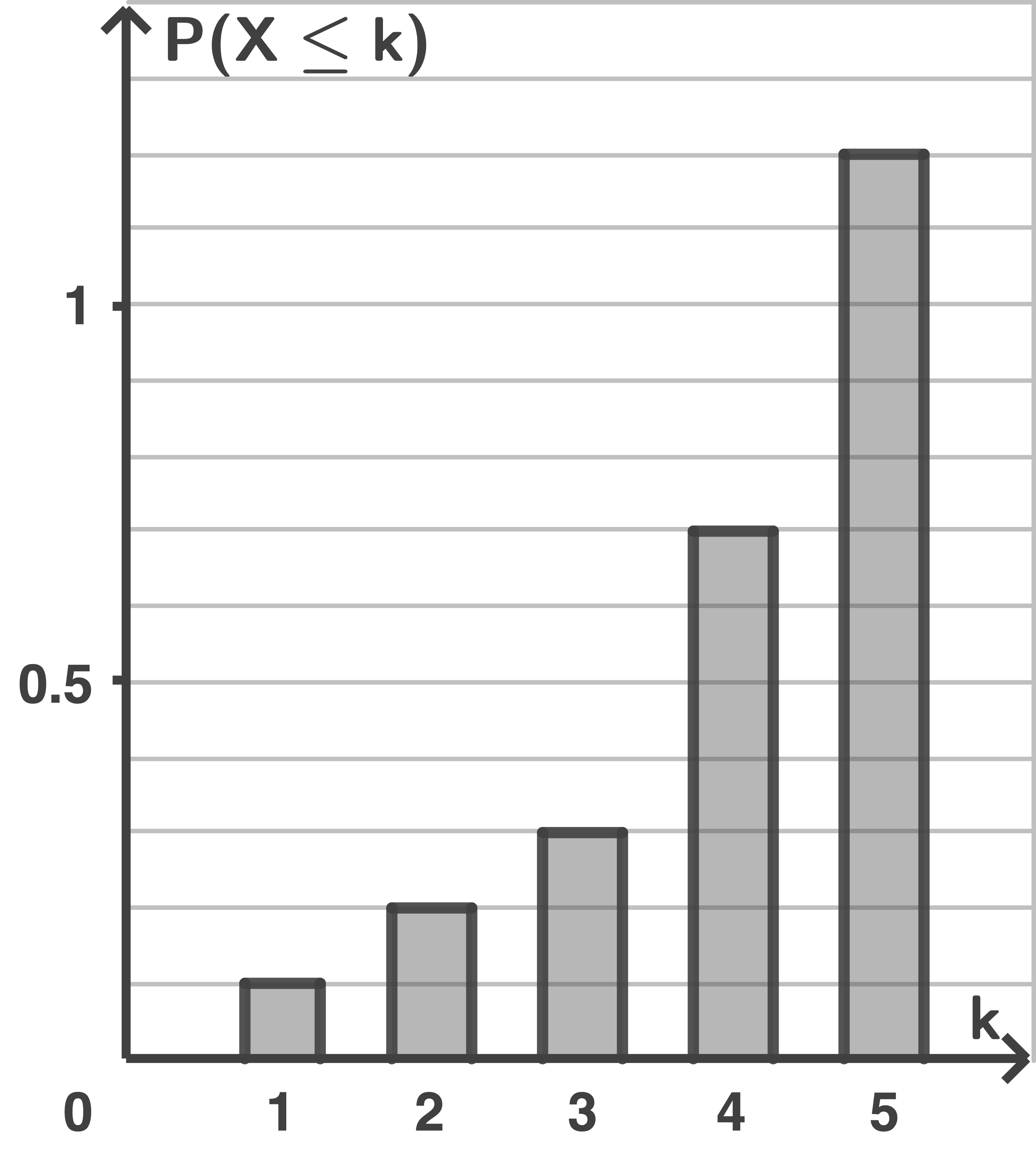
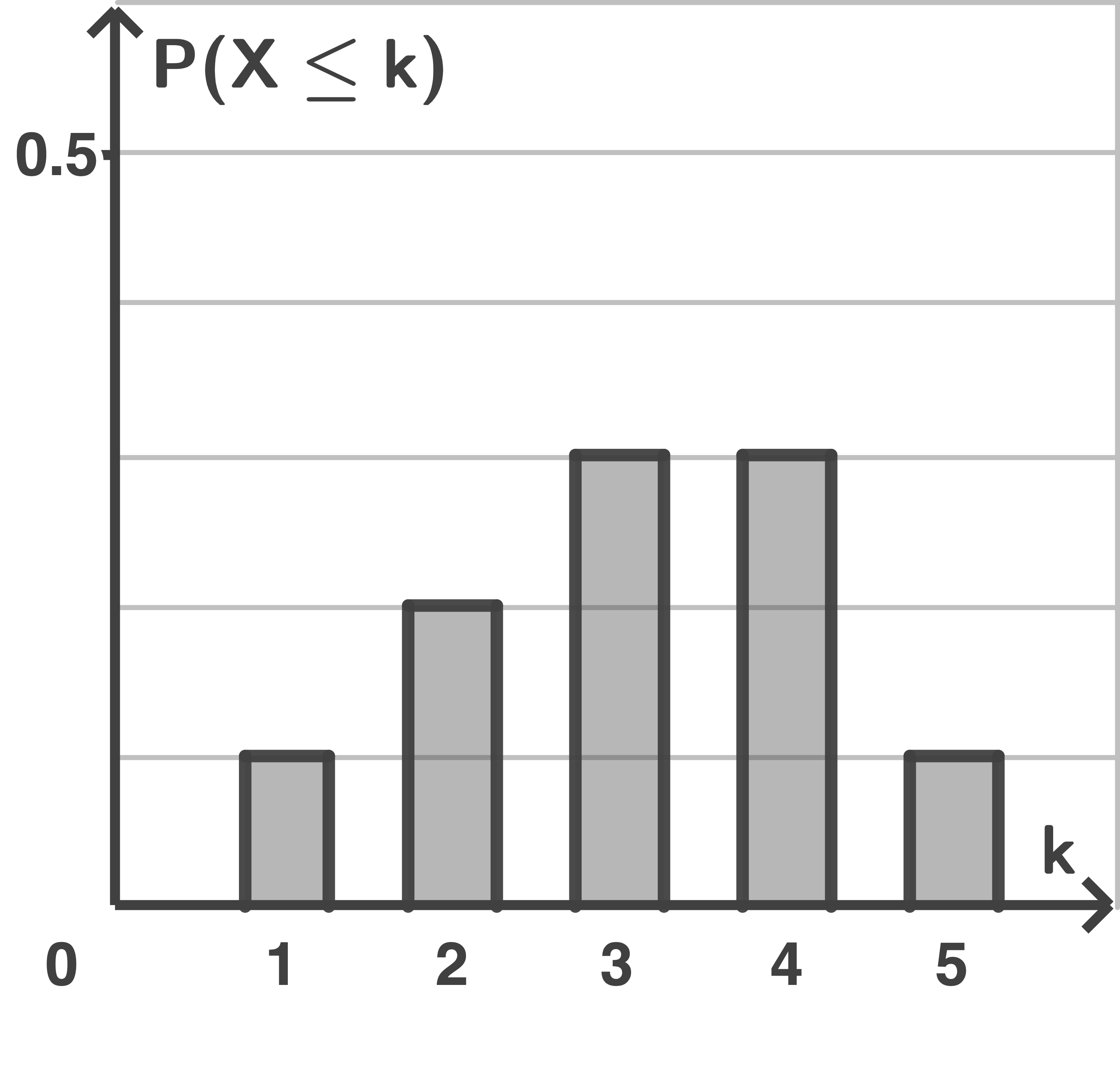
Begründe jeweils, dass in den Abbildungen nicht die Werte für die summierte (kumulierte) Wahrscheinlichkeitsverteilung von $X$ dargestellt wurden.

Balkendiagramm, das die kumulative Wahrscheinlichkeit P(X ≤ k) für verschiedene Werte von k zeigt.

Abb.1

Grafik zur Darstellung der kumulativen Wahrscheinlichkeit P(X ≤ k) in einem Diagramm.

Abb. 2

(2 BE)

4.2

Gegeben ist eine binomialverteilte Zufallsgröße $Y$ mit der Anzahl der Durchführungen $n=3$ und einer Trefferwahrscheinlichkeit $p\gt0$ .
Es gilt: $P(Y=2)=3 \cdot P(Y=3)$
Berechne den Wert von $p$ .

(3 BE)

1.1

$f(x)= \dfrac{1}{x^2}+2=x^{-2}+2$

$\(f$

Berechne die Steigung $m_t:$

$\(\begin{array}[t]{rll} f$

Berechne die $y-$ Koordinate von $P:$

$\begin{array}[t]{rll} f(1)&=&\dfrac{1}{1^2}+2 &\quad \\[5pt] &=&3 \end{array}$

Setze die Werte in die allgemeine Tangentengleichung ein:

$\begin{array}[t]{rll} y&=&m\cdot x+n &\quad \\[5pt] 3&=&-2\cdot1+n &\quad \scriptsize \mid\;+2 \\[5pt] 5&=&n &\quad\\[5pt] \end{array}$

$t: y=-2x+5$

1.2

Die Tangente und Normale sind immer senkrecht zueinader, wodurch sie einen Innenwinkel, der $90^\circ$ beträgt, bilden.
Eine Eigenschaft im gleichseitigen Dreieck ist, dass alle Innenwinkel $60^\circ$ betragen.
Dies ist ein Widerspruch. Deshalb kann das Dreieck, welches durch $t$ , $s$ und die $x-$ Achse gebildet wird, nicht gleichseitig sein.

Skizze zur Veranschaulichung:

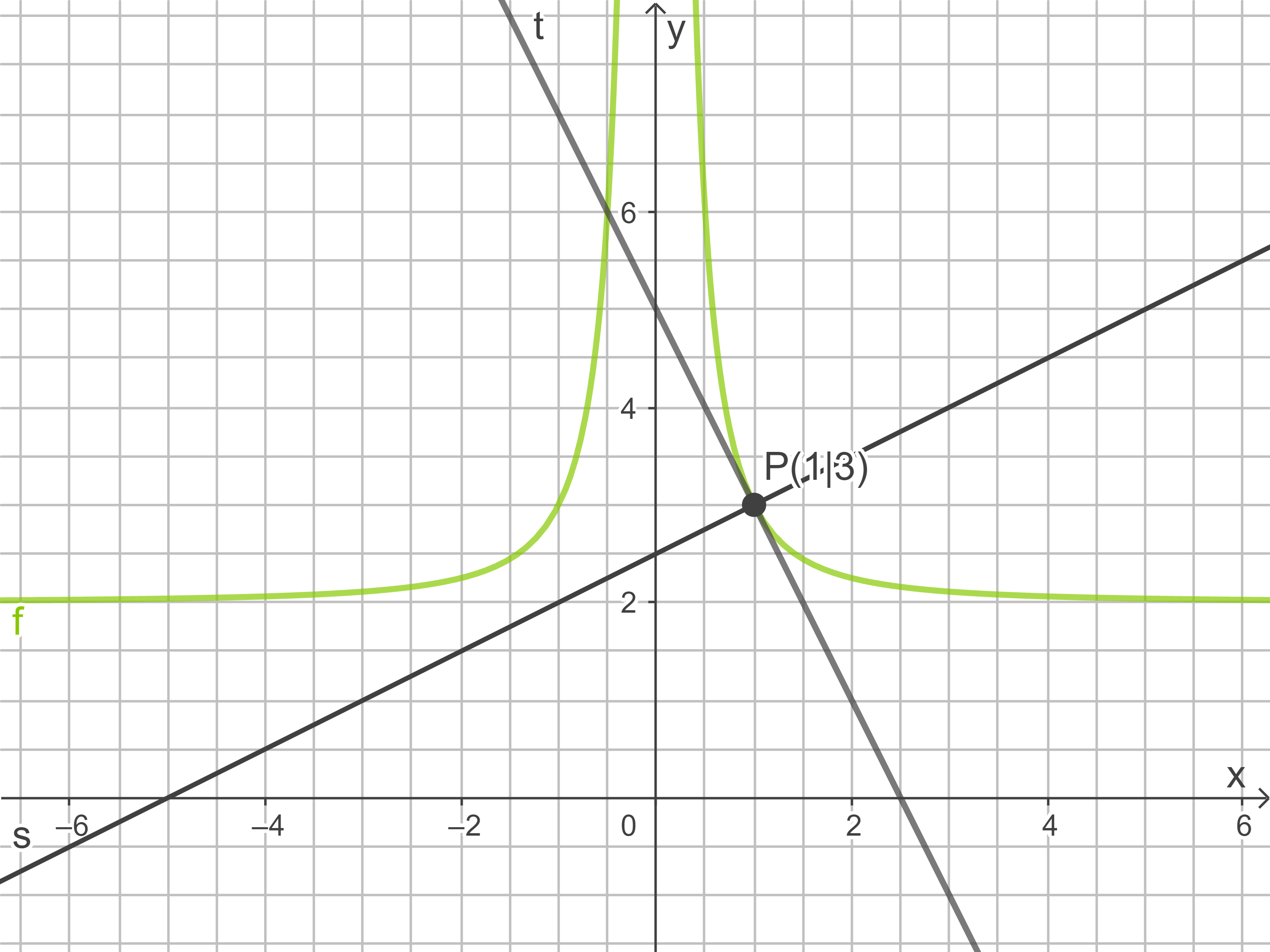
Grafik eines Koordinatensystems mit verschiedenen Linien und einem Punkt P(1/3).

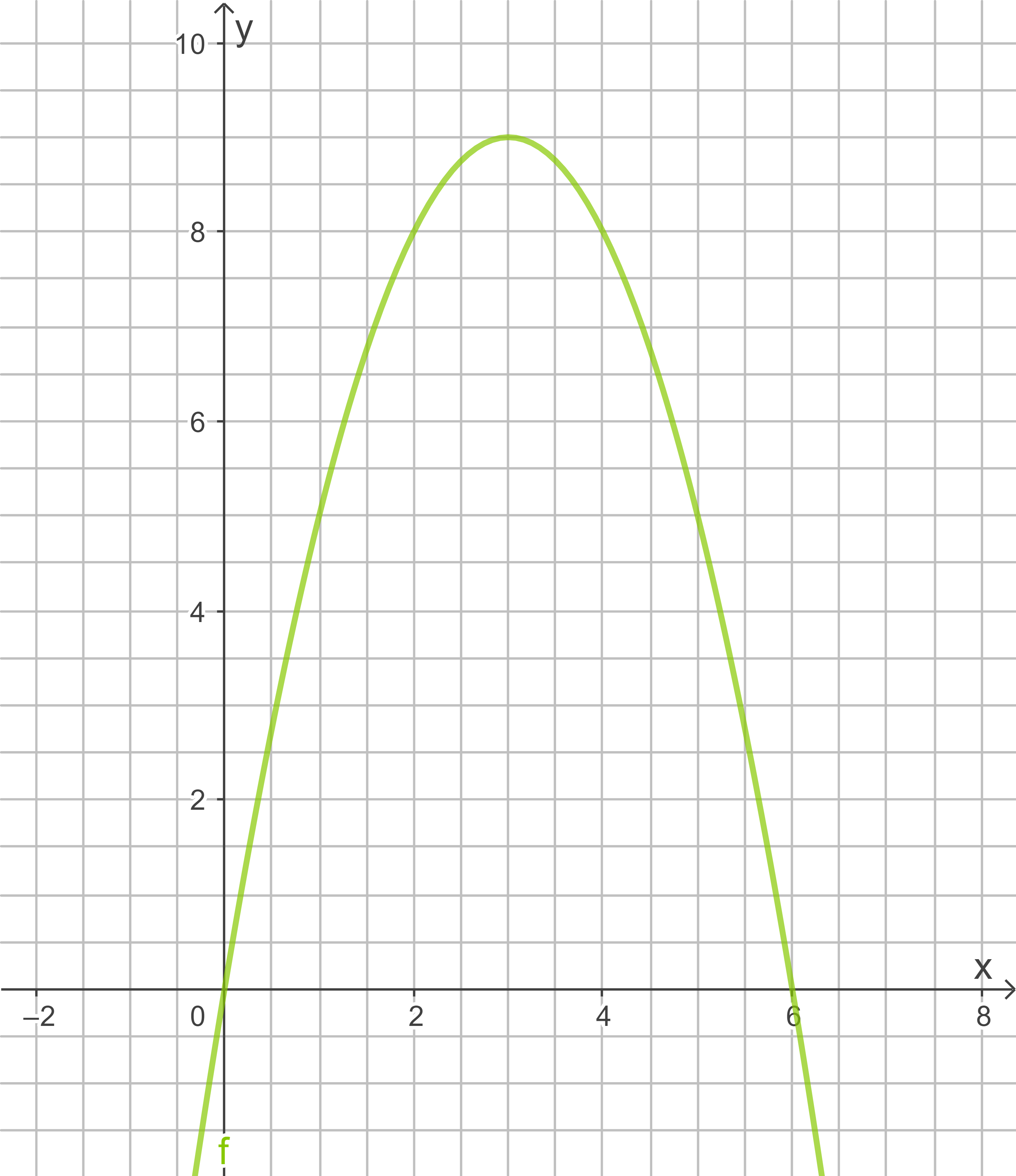
2.1

Die Schuppe ist parabelförmig, daher ist die Funktion quadratisch:

$f(x)=ax^2+bx+c$

Am Graphen kann man drei Punkte ablesen:

Zwei Nullstellen: $P_1(0 \mid 0)$ und $P_2(6 \mid 0)$
Scheitelpunkt: $S(3 \mid 9)$

$\begin{array}[t]{rll} f(0)&=&0 & \\[5pt] f(6)&=&0 \\[5pt] f(3)&=&9 \end{array}$

$\begin{array}[t]{rll} 0&=&a \cdot 0^2+b \cdot 0+c \Rightarrow c=0\\[5pt] 0&=&a \cdot 6^2+b \cdot 6 \\[5pt] 9&=&a \cdot 3^2+b \cdot 3 \end{array}$

2. Gleichung nach $b$ auflösen:
$\begin{array}[t]{rll} 0&=&36a+6b &\quad \scriptsize \mid\;-6b \\[5pt] -6b&=&36a &\quad \scriptsize \mid\;:(-6) \\[5pt] b&=&-6a \end{array}$

$b$ in die 3. Gleichung einsetzen:
$\begin{array}[t]{rll} 9&=&9a+3 \cdot (-6a) \\[5pt] 9&=&9a-18a \\[5pt] 9&=&-9a &\quad \scriptsize \mid\;:(-9)\\[5pt] -1&=&a \end{array}$

$a$ einsetzen:
$\begin{array}[t]{rll} b&=&-6 \cdot(-1) \\[5pt] b&=&6 \\[5pt] \end{array}$

Funktionsgleichung: $f(x)=-x^2 +6x$

2.2

Berechnung des Flächeninhalts einer Schuppe
$\Rightarrow$ Berechnung des Integrals:

Diagramm einer grünen Kurve in einem Koordinatensystem mit Achsenbeschriftungen.

Stammfunktion: $F(x)= -\dfrac{1}{3}x^3+3x^2$

$\begin{array}[t]{rll} \displaystyle\int_{0}^{6}(-x^2+6x)\;\mathrm dx&=&\bigg[-\dfrac{1}{3}x^3+3x^2 \bigg]_0 ^6 \\[5pt] &=&\dfrac{1}{3}\cdot 6^3+ 3 \cdot 6^2 -0 \\[5pt] &=&36 \end{array}$

$\dfrac{18.000\;\text{mm}^2}{36\;\text{mm}^2}= 500$

Antwort:
Ungefähr $500$ Schuppen würden einen $18.000\,\text{mm}^2$ großen Hautbereich bedecken.

3.1

Die Ebene $E:3y+4z=24$ besitzt den Normalenvektor $\overrightarrow{n_E}=\pmatrix{0\\3\\4}$ .

Die $x-$ Achse lässt sich beschreiben als $\overrightarrow{x}=\pmatrix{1\\0\\0}$ .

Berechne das Skalarprodukt:

$\overrightarrow{n_E} \circ \overrightarrow{x}=\pmatrix{0\\3\\4}\circ \pmatrix{1\\0\\0}$ $=0 \cdot 1+3 \cdot 0+4 \cdot 0=0\Rightarrow$ parallel

3.2

$E:3y+4z=24$

$xy-$ Ebene: $z=0$

Berechne die Schnittgerade, indem du $E_{xy}$ in $E$ einsetzt:

$\begin{array}[t]{rll} 3y+4\cdot0&=&24 &\quad \scriptsize \mid\;:3 \\[5pt] y&=&8 \end{array}$

Die Ebene $E$ und die $xy-$ Ebene schneiden sich in der Geraden $g$ mit der Gleichung $y=8.$

Für $t=8$ liegt der Punkt $D_t$ auf $g.$
Für $t\gt8$ befinden sich $A$ und $D_T$ auf verschiedenen Seiten von $E$ .
Für $t\lt8$ liegen alle Eckpunkte der Pyramide auf der gleichen Seite.

Die Pyramide und $E$ haben gemeinsame Punkte, wenn $t\geq8$ gilt.

4.1

Abbildung 1:

Kann nicht sein, da $P(X\leq5)\gt1.$

Abbildung 2:

Da $P(X\leq5)\geq P(X\leq4)$ sein muss.

4.2

Da die Zufallsgröße $Y$ binomialverteilt ist, kann man die Formel von Bernoulli anwenden:

Formel von Bernoulli:
$P(X=k)=\pmatrix{n\\k} \cdot p^k \cdot (1-p)^{n-k}$

$P(Y=2)=\pmatrix{3\\2} \cdot p^2 \cdot (1-p)$ $=3 \cdot p^2 \cdot (1-p)$
$P(Y=3)=\pmatrix{3\\3} \cdot p^3 \cdot (1-p)^0$ $=p^3$

Es gilt: $P(Y=2)=3 \cdot P(Y=3)$

$\begin{array}[t]{rll} 3 \cdot p^2 \cdot (1-p)&=&3 \cdot p^3 &\quad \scriptsize \mid\;:3\\[5pt] p^2 \cdot (1-p)&=&p^3 &\quad \scriptsize \mid\;-p^3\\[5pt] p^2 \cdot (1-p)-p^3&=&0 \\[5pt] p^2-2p^3&=&0 \\[5pt] p^2 \cdot (1-2p)&=&0 \\[5pt] \end{array}$

Satz des Nullprodukts:

$\begin{array}[t]{rll} p^2&=&0 &\quad \scriptsize \mid\;\sqrt{\quad} \\[5pt] p&=&0 \Rightarrow p\gt0 \end{array}$

$\begin{array}[t]{rll} 1-2p&=&0 &\quad \scriptsize \mid\;-1 \\[5pt] -2p&=&-1 &\quad \scriptsize \mid\;:(-2) \\[5pt] p&=&\dfrac{1}{2} \end{array}$

Da für die Trefferwahrscheinlichkeit $p\gt0$ gilt, ist $p=\frac{1}{2}$ die einzige Lösung.