2. Analytische Geometrie

Betrachtet wird die Pyramide $ABCDS_k$ mit $A(0\mid 0\mid0)$ , $B(2\mid0\mid0)$ , $C(2\mid2\mid0)$ , $D(0\mid2\mid0)$ und $S_k(1\mid 1\mid k)$ mit $k \in ]1;+\infty[$ .
Die gemeinsame Grundfläche $ABCD$ dieser Pyramiden ist quadratisch. Der abgebildete Punkt $T$ ist der Schnittpunkt der Diagonalen der Grundfläche $ABCD$ .
Die Abbildung zeigt beispielhaft eine dieser Pyramiden.

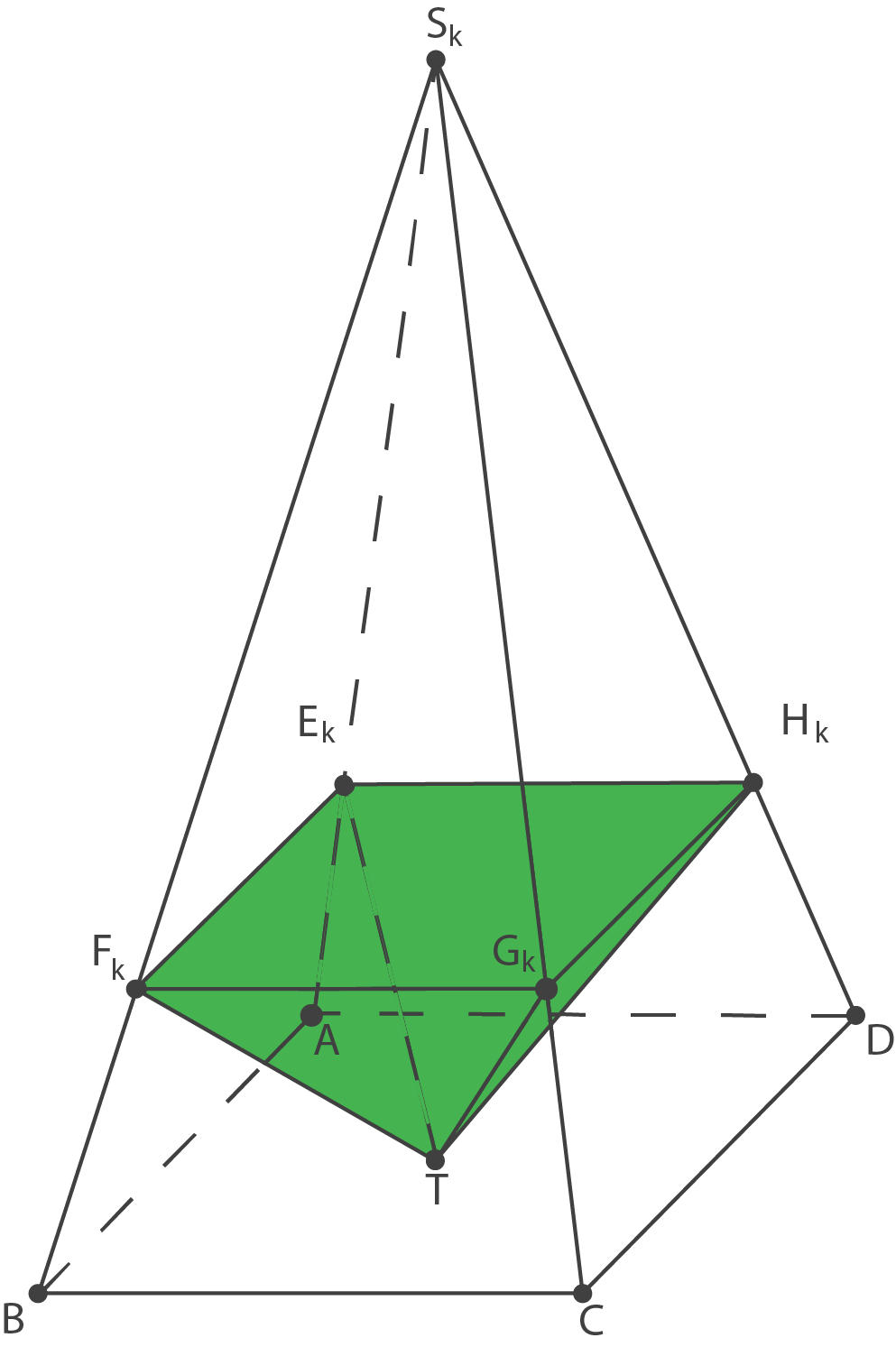
3D-Diagramm eines geometrischen Körpers mit markierten Punkten und einer grünen Fläche.

2.1

Begründe, dass jede der Pyramiden $ABCDS_k$ gerade ist.
Berechne den Inhalt der Mantelfläche der Pyramide $ABCDS_k$

(5 BE)

2.2

Begründe, dass die Gleichung $\overrightarrow{x}=\pmatrix{2\\0\\0}+\lambda \cdot \pmatrix{-1\\1\\0}+ \mu \cdot \pmatrix{0\\1\\1}$ mit $\lambda, \mu \in \mathbb{R}$ keine Symmetrieebene der Pyramide $ABCDS_k$ beschreibt.
Gib für eine Symmetrieebene der Pyramide $ABCDS_k$ eine Gleichung in Koordinatenform an.

(3 BE)

2.3

Die Seitenfläche $ABS_k$ liegt in der Ebene $L$ .
Bestimme eine Gleichung von $L$ in Koordinatenform.
[zur Kontrolle: $k \cdot y-z=0$ ]

(3 BE)

2.4

Bestimme denjenigen Wert von $k$ , für den die Seitenfläche $ABS_k$ gegenüber der Grundfläche $ABCD$ um einen Winkel der Größe $60^{\circ}$ geneigt ist.

(3 BE)

2.5

Der Mittelpunkt der Strecke $\overline{TS_k}$ wird mit $Q_k$ bezeichnet. Für einen Wert von $k$ ist $Q_k$ von der Grundfläche $ABCD$ dreimal so weit entfernt wie von jeder der vier Seitenflächen der Pyramide $ABCDS_k$ . Berechne diesen Wert von $k$ .

(4 BE)

2.6

Die Ebene mit der Gleichung $z=1$ schneidet die vier vom Punkt $S_k$ ausgehenden Kanten der Pyramide $ABCDS_k$ in den Punkten $E_k$ , $F_k$ , $G_k$ und $H_k$ (vgl. Abbildung).

2.6.1

Bestimme die $x$ - und $y$ -Koordinate von $F_k$ .

(3 BE)

2.6.2

Bestimme diejenigen Werte von $k$ , für die das Verhältnis des Volumens der Pyramide $E_kF_kG_kH_kT$ zum Volumen der Pyramide $ABCDS_k$ $1:8$ beträgt.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

1. Schritt: Begründen, warum jede Pyramide $ABCDS_k$ gerade ist.

die Grundfläche liegt in der xy-Ebene
der Schnittpunkt der Diagonalen hat die gleichen x- und y-Koordinaten wie $S_k$

2. Schritt: Inhalt der Mantelfläche berechnen.
Mittelpunkt $M\left(2\mid1\mid0\right)$ von $\overline{BC}$
$\begin{array}[t]{rlll} & & 4 \cdot \frac{1}{2} \cdot 2 \cdot \mid \overline{MS_k} \mid & \quad \scriptsize \\[5pt] &=& 4 \cdot \sqrt{1+k^2} & \quad \scriptsize \\[5pt] \end{array}$

2.2

1. Schritt: Begründen, dass die gegebene Gleichung keine Symmetrieebene der Pyramide $ABCDS_k$ beschreibt.

1.1 Schritt: Die gegebenen Gleichung analysieren.
Du kannst die Gleichung $\overrightarrow{x}=\pmatrix{2\\0\\0}+\lambda \cdot \pmatrix{-1\\1\\0}+ \mu \pmatrix{0\\1\\1}$ komponentenweise betrachten, um Aussagen über ihre Eigenschaften zu treffen.
Der erste Vektor entspricht dem Ortsvektor von $\overrightarrow{OB}$ . Ausgehend von $B$ zeigt der zweite Vektor auf den Punkt $T$ . Der Faktor $\lambda$ skalliert die Länge des Vektors.
Somit kann die Gerade durch $B$ und $D$ durch $g_{BD}: \overrightarrow{x}= \pmatrix{2\\0\\0}+\lambda \cdot \pmatrix{-1\\1\\0}$ mit $\lambda \in \mathbb{R}$ beschrieben werden.

1.2 Schritt: Begründen was die Beschreibung einer Symmetrieebene verhindert.
Damit die, in der Aufgabenstellung gegebene, Gleichung eine Symmetrieebenene der Pyramide $ABCDS_k$ beschreibt, müsste der Vektor $\pmatrix{0\\1\\1}$ parallel zu einer Symmetrieebene sein, welche die Gerade $g_{BD}$ enthält. Das ist nicht der Fall. Die Symmetrieebene, welche die Gerade $g_{BD}$ enthält teilt die Pyramide diagonal.

2. Schritt: Koordinatenform einer Symmetrieebene der Pyramide $ABCDS_k$ angeben.
Eine einfach anzugebene Koordinatenform einer Symmetrieebene der Pyramide $ABCDS_k$ ist $x=1$ . Diese Symmetrieebene teilt die Pyramide bei $x=1$ in zwei Hälften.

2.3

1. Schritt: den Normalenvektor der Ebene $L$ bestimmen.
Der Normalenvektor steht senrecht zu den Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AS_k}$ , welche die Ebene $L$ aufspannen.

Sei $\overrightarrow{n}=\pmatrix{n_1\\n_2\\n_3}$ .

$n_1 = 0$

Vollständige Lösung anzeigen

$-n_2= n_3\cdot k$

Vollständige Lösung anzeigen

Um einen Normalenvektor zu erhalten, musst du nun eine Kombination von $n_1$ und $n_3$ finden, welche die obrige Gleichung erfüllt. Dies ist der Fall bei $n_2=k$ und $n_3=-1$ .
Der Normalenvektor kann also durch $\overrightarrow{n}=\pmatrix{0\\k\\-1}$ angegeben werden.

3. Schritt: Normalenform der Ebene $L$ aufstellen.

$0= \pmatrix{x\\y\\z}\circ\pmatrix{0\\k\\-1}$

Vollständige Lösung anzeigen

4. Schritt: Koordinatenform aus der Normalenform folgern.
$\begin{array}[t]{rlll} 0&=& x\cdot 0+y\cdot k+z\cdot(-1) & \quad \scriptsize \\[5pt] 0&=& y\cdot k-z & \quad \scriptsize \\[5pt] \end{array}$

Damit folgt: $L: k \cdot y-z=0$ .

2.4

$k= \pm\sqrt{3}$

Vollständige Lösung anzeigen

Da $k \in ] 1;+\infty[$ gilt, ist $k=\sqrt{3}$ , wenn die Seite $ABS_k$ gegenüber der Grundfläche $ABCD$ um $60^{\circ}$ geneigt ist.

2.5

Der Mittelpunkt der Strecke $\overline{TS_k}$ ist $Q_k\left(1\mid1\mid\frac{k}{2}\right)$ . Es gilt:

$k=\pm 2\sqrt{2}$

Vollständige Lösung anzeigen

Daraus folgt, dass $k=2\sqrt{2}$ ist, da k positiv sein muss, weil $S_k$ oberhalb der x-Achse liegt.

2.6.1

1. Schritt: Parametergleichung aufstellen.
$\pmatrix{x\\y\\z}=\pmatrix{2\\0\\0}+\sigma \cdot \pmatrix{-1\\1\\k}$

2. Schritt: Gleichungen ablesen.

$x=2-\sigma$
$y=\sigma$
$z=\sigma \cdot k$

3. Schritt: Gleichungen ineinander einsetzen.
Mit $z=1$ folgt aus der $3.$ Gleichung:
$\begin{array}[t]{rlll} z&=&\sigma \cdot k & \quad \scriptsize \mid z=1\\[5pt] 1&=&\sigma \cdot k & \quad \scriptsize \mid :k\\[5pt] \sigma&=&\frac{1}{k} & \quad \scriptsize \\[5pt] \end{array}$

Damit sind die x- und y-Koordinaten von $F_k$ : $x=2-\sigma=2-\frac{1}{k}$ und $y=\frac{1}{k}$

2.6.2

Da die Dreiecke $ABS_k$ und $E_kF_kS_k$ ähnlich zueinander sind, gilt: $\begin{array}[t]{rlll} \frac{\overline{E_kF_k}}{\overline{AB}} &=& \frac{k-1}{k} & \quad \scriptsize \\[5pt] \end{array}$

1. Schritt: Die Punkte $E_k$ und $F_k$ bestimmen.
Aus der vorherigen Aufgabe $2.6.1$ folgt der Punkt $F_k\left(2-\frac{1}{k}\mid \frac{1}{k} \mid 1\right)$ .
Der Punkt $E_k$ hat die gleichen y- und z-Koordinaten wie $F_k$ . Die x-Koordinate von $E_k$ ist $0-\frac{1}{k}$ . Damit ist $E_k\left(\frac{1}{k}\mid \frac{1}{k} \mid 1\right)$ .

2. Schritt: k bestimmen.
Für das Verhältnis der Pyramiden zueinander gilt: