Wahlteil A3
A3 Stochastik
Die Verwaltung einer Stadt in Mecklenburg-Vorpommern gab als Veranstalter eines Volksfestes 2008 eine repräsentative Umfrage in Auftrag, die über Wirtschaftswert des Volksfestes, Beucherstruktur, Image und Unterhaltungswert Auskunft geben sollte.Die überwiegende Mehrheit der Festbesucher kam mit
3.1
Bei der Umfrage wurden zwei Besucher nach ihrem Herkunftsort mit den Antwortmöglichkeiten  ,
,  ,
,  befragt.
Stelle für dieses Zufallsexperiment ein vollständiges Baumdiagramm auf und gib eine Ergebnismenge
befragt.
Stelle für dieses Zufallsexperiment ein vollständiges Baumdiagramm auf und gib eine Ergebnismenge  an.
an.
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
: Beide Besucher stammen aus Mecklenburg-Vorpommern.
: Mindestens ein Besucher kommt aus dem Ausland.
3.2
Die Zufallsgröße  beschreibt die Anzahl der ausländischen Besucher bei einer Befragung von
beschreibt die Anzahl der ausländischen Besucher bei einer Befragung von  Personen.
Begründe, dass
Personen.
Begründe, dass  als binomialverteilt angesehen werden kann.
als binomialverteilt angesehen werden kann.
Berechne für jeden Wert von die Wahrscheinlichkeit und stelle diese Wahrscheinlichkeitsverteilung grafisch dar.
die Wahrscheinlichkeit und stelle diese Wahrscheinlichkeitsverteilung grafisch dar.
Berechne für jeden Wert von
3.3
Vier Besucher wurden bezüglich ihrer Anfahrt befragt. Ein Großteil der Besucher benutzte öffentliche Verkehrsmittel ( ), die anderen private Fahrzeuge (
), die anderen private Fahrzeuge ( ).
Gib die folgenden Ereignisse als Teilmengen der Ergebnismenge an.
).
Gib die folgenden Ereignisse als Teilmengen der Ergebnismenge an.
 in Worten.
in Worten.
: Genau drei Personen fahren mit einem privaten Fahrzeug.
: Die dritte Person fährt mit öffentlichen Verkehrsmitteln.
3.4
Das Volksfest war ein Fest für alle Generationen, Jung und Alt feierten gemeinsam. So hatte die Altersgruppe „30 Jahre und älter“ einen Anteeil von  . Weibliche Besucher waren mit
. Weibliche Besucher waren mit  vertreten. Rund
vertreten. Rund  aller Festbesucher waren Kinder (untr 14 Jahre).
aller Festbesucher waren Kinder (untr 14 Jahre).
3.4.1
Man geht bei der Befragung davon aus, dass die Eigenschaften „Geschlecht“ und „Alter“ voneinander unabhängig sind.
Berechne die Wahrscheinlichkeit dafür, dass bei einer Befragung die Person
Am Eingang einer bei allen Festbesuchern besonders beliebten Attraktion wird geprüft, wie viele der Besucher Kinder sind.
- männlich und „unter 30“ ist.
- weiblich und nicht „unter 30“ ist.
3.4.2
Es werden  Besucher dieser Attraktion befragt. Die Befragung kann als Bernoulli-Kette aufgefasst werden.
Mit wie vielen Kindern muss bei der Prüfung gerechnet werden?
Besucher dieser Attraktion befragt. Die Befragung kann als Bernoulli-Kette aufgefasst werden.
Mit wie vielen Kindern muss bei der Prüfung gerechnet werden?
Berechne die Wahrscheinlichkeit dafür, dass unter den Befragten
Befragten
Berechne die Wahrscheinlichkeit dafür, dass unter den
- genau
Kinder sind.
- mindestens
, aber weniger als
Kinder gefunden werden.
3.4.3
Berechne, wie viele Personen befragt werden müssen, um mit einer Wahrscheinlichkeit von mehr als  mindestens zwei Kinder unter den Besuchern zu finden.
mindestens zwei Kinder unter den Besuchern zu finden.
3.1
: Mecklenburg-Vorpommern
: Eins der übrigen deutschen Bundesländer
: Ausland
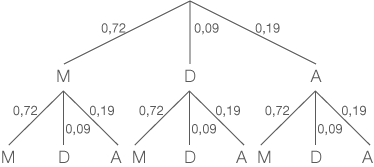 Abb. 1: Baumdiagramm
Abb. 1: Baumdiagramm
3.2
- In jedem Durchgang gibt es nur zwei mögliche Ausgänge: „Erfolg“ oder „Misserfolg“
- In jedem Durchgang bleibt die Wahrscheinlichkeit für einen Erfolg gleich.
Im Einführungstext der Aufgabe ist angegeben, dass die Umfrage repräsentativ ist. Dies beinhaltet, dass eine hinreichend große Menschenmenge befragt wird, sodass die Wahrscheinlichkeiten für die verschiedenen Herkunftsländer bei jeder Person annähernd gleich bleibt, unabhängig davon, wie viele schon befragt wurden. Bei jeder der
Außerdem wird hier nur noch zwischen zwei Möglichkeiten unterschieden: „Kommt aus dem Ausland“ oder „Kommt nicht aus dem Ausland“. Beide Bedingungen sind also erfüllt, sodass
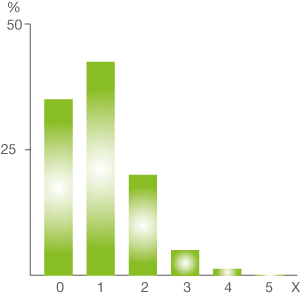 Abb. 2: Wahrscheinlichkeitsverteilung
Abb. 2: Wahrscheinlichkeitsverteilung
3.3
3.4.1
Die Wahrscheinlichkeit dafür, dass zwei voneinander unabhängige Ereignisse
3.4.2
Du weißt aus der Aufgabenstellung, dass die Befragung als Bernoulli-Kette aufgefasst werden kann. Das bedeutet, dass
Zuerst ist die Wahrscheinlichkeit für genau  Kinder gesucht, also
Kinder gesucht, also  . Verwende dazu den binomPdf-Befehl deines CAS. Diesen findest du unter:
. Verwende dazu den binomPdf-Befehl deines CAS. Diesen findest du unter:
 ,
,  und
und  eingeben und erhältst dann folgendes Ergebnis:
eingeben und erhältst dann folgendes Ergebnis:
menu  5
5  5
5  D: BinomialPdf
D: BinomialPdf
Du musst dort die Parameter 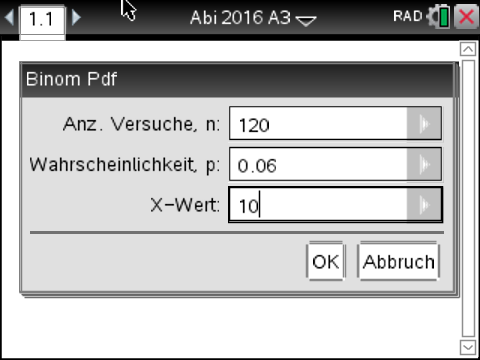 Abb. 3: Eingabe der Parameter
Abb. 3: Eingabe der Parameter
3.4.3
Diese Ungleichung kannst du mit dem solve-Befehl deines CAS lösen und erhältst folgendes Ergebnis:
 oder
oder  Das zweite Ergebnis ergibt aber im Sachzusammenhang keinen Sinn, da es keine negative Anzahl an Personen geben kann.
Das zweite Ergebnis ergibt aber im Sachzusammenhang keinen Sinn, da es keine negative Anzahl an Personen geben kann.
 Abb. 4: Lösen der Gleichung
Abb. 4: Lösen der Gleichung
© 2017 - SchulLV.
3.1
: Mecklenburg-Vorpommern
: Eins der übrigen deutschen Bundesländer
: Ausland
 Abb. 1: Baumdiagramm
Abb. 1: Baumdiagramm
3.2
- In jedem Durchgang gibt es nur zwei mögliche Ausgänge: „Erfolg“ oder „Misserfolg“
- In jedem Durchgang bleibt die Wahrscheinlichkeit für einen Erfolg gleich.
Im Einführungstext der Aufgabe ist angegeben, dass die Umfrage repräsentativ ist. Dies beinhaltet, dass eine hinreichend große Menschenmenge befragt wird, sodass die Wahrscheinlichkeiten für die verschiedenen Herkunftsländer bei jeder Person annähernd gleich bleibt, unabhängig davon, wie viele schon befragt wurden. Bei jeder der
Außerdem wird hier nur noch zwischen zwei Möglichkeiten unterschieden: „Kommt aus dem Ausland“ oder „Kommt nicht aus dem Ausland“. Beide Bedingungen sind also erfüllt, sodass
 Abb. 2: Wahrscheinlichkeitsverteilung
Abb. 2: Wahrscheinlichkeitsverteilung
3.3
3.4.1
Die Wahrscheinlichkeit dafür, dass zwei voneinander unabhängige Ereignisse
3.4.2
Du weißt aus der Aufgabenstellung, dass die Befragung als Bernoulli-Kette aufgefasst werden kann. Das bedeutet, dass
Du sollst die Wahrscheinlichkeiten für verschiedene Ereignisse berechnen, die sich auf die Anzahl der Kinder unter den  Befragten beziehen. Du kannst dafür also die binomialverteilte Zufallsvariable
Befragten beziehen. Du kannst dafür also die binomialverteilte Zufallsvariable  wie oben verwenden.
Für die Berechnung kannst du dein CAS verwenden.
Zuerst ist die Wahrscheinlichkeit für genau
wie oben verwenden.
Für die Berechnung kannst du dein CAS verwenden.
Zuerst ist die Wahrscheinlichkeit für genau  Kinder gesucht, also
Kinder gesucht, also  . Verwende dazu den binomPdf-Befehl deines CAS. Diesen findest du im Statistik-Menü unter:
. Verwende dazu den binomPdf-Befehl deines CAS. Diesen findest du im Statistik-Menü unter:
 ,
,  und
und  eingeben und erhältst dann folgendes Ergebnis:
eingeben und erhältst dann folgendes Ergebnis:
Calc  Verteilungen
Verteilungen  Binom. Einzelwkt.
Binom. Einzelwkt.
Du musst dort die Parameter 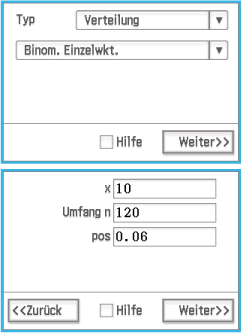 Abb. 3: Eingabe der Parameter
Abb. 3: Eingabe der Parameter
3.4.3
Diese Ungleichung kannst du mit dem solve-Befehl deines CAS lösen und erhältst folgendes Ergebnis:
 oder
oder  Das zweite Ergebnis ergibt aber im Sachzusammenhang keinen Sinn, da es keine negative Anzahl an Personen geben kann.
Das zweite Ergebnis ergibt aber im Sachzusammenhang keinen Sinn, da es keine negative Anzahl an Personen geben kann.
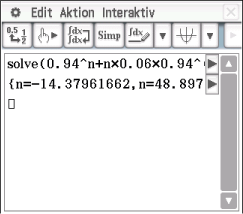 Abb. 4: Lösen der Gleichung
Abb. 4: Lösen der Gleichung
© 2017 - SchulLV.