Analytische Geometrie
Analytische Geometrie
2.
Die Eckpunkte eines Holzkörpers werden durch  ,
,  ,
,  ,
,  und
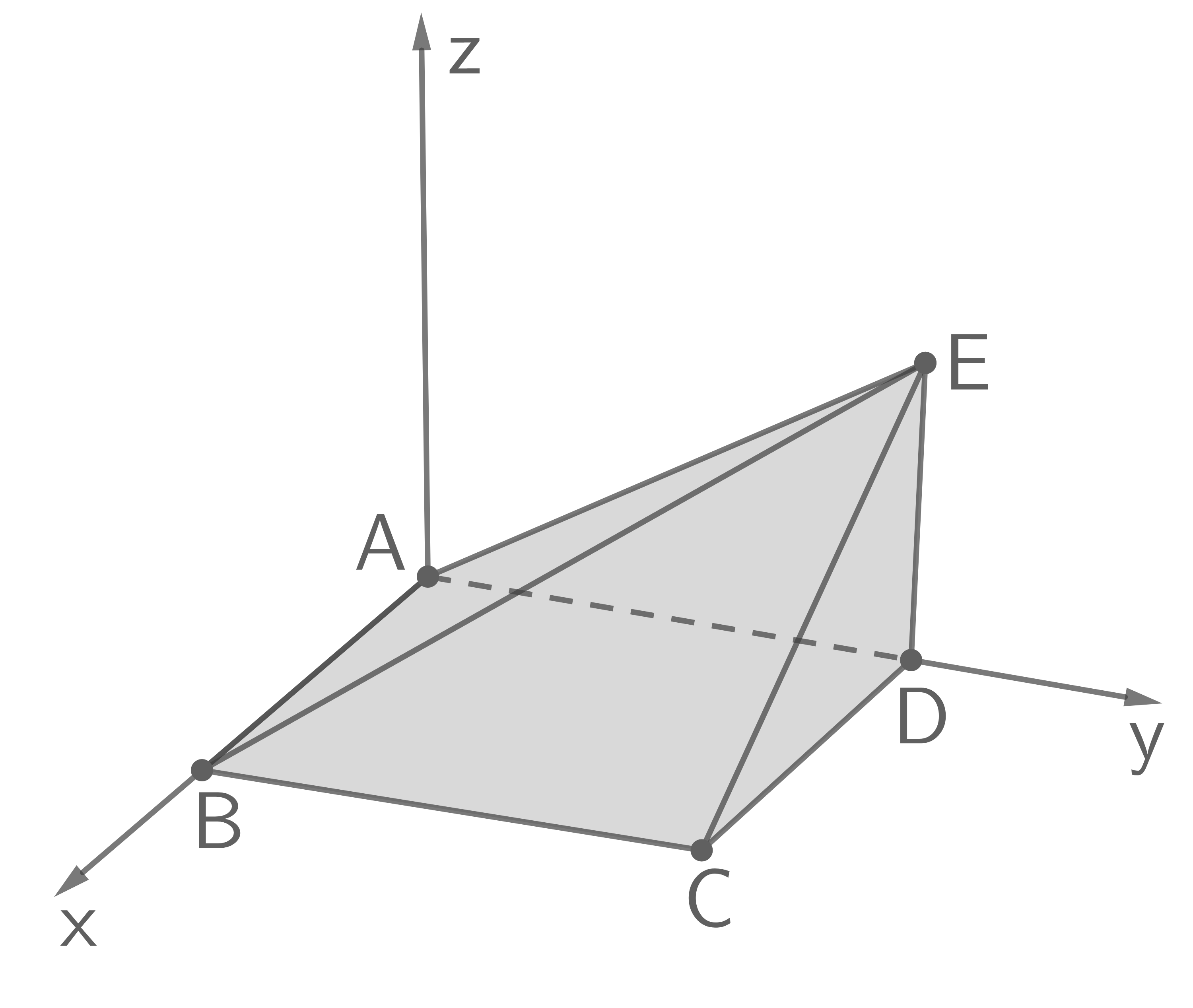
und  dargestellt (vgl. Abbildung).
dargestellt (vgl. Abbildung).
Die Punkte B, D und E liegen im Modell in der Symmetrieebene des Körpers.
Eine Längeneinheit im Koordinatensystem entspricht einem Zentimeter in der Realität.
Die Punkte B, D und E liegen im Modell in der Symmetrieebene des Körpers.
Eine Längeneinheit im Koordinatensystem entspricht einem Zentimeter in der Realität.
2.1
Zeige, dass das Dreieck BCE rechtwinklig ist, und berechne den Inhalt der Oberfläche des Holzkörpers.
(5 BE)
2.2
Bestimme eine Gleichung der Ebene L, in der das Dreieck BCE liegt, in Koordinatenform.
(3 BE)
2.3
Die quadratische Grundfläche des Holzkörpers schließt mit der Seitenfläche, die durch das Dreieck BCE dargestellt wird, einen Winkel ein.
Berechne die Größe dieses Winkels.
Berechne die Größe dieses Winkels.
(2 BE)
2.4
Der Holzkörper soll mit einer möglichst kurzen Linie versehen werden, die im Modell vom Eckpunkt A über die Kante  zum Punkt C verläuft. Die Länge dieser Linie in Zentimetern kann folgendermaßen ermittelt werden:
zum Punkt C verläuft. Die Länge dieser Linie in Zentimetern kann folgendermaßen ermittelt werden:



Erläutere dieses Vorgehen.
Erläutere dieses Vorgehen.
(4 BE)
2.5
Der Schnittpunkt der Ebene L mit der  -Achse wird mit F bezeichnet.
-Achse wird mit F bezeichnet.
2.5.1
Zeichne F sowie die Geraden, in denen L die  - und die
- und die  -Ebene schneidet, in die Abbildung ein.
-Ebene schneidet, in die Abbildung ein.
(2 BE)
2.5.2
Ermittle, um wie viel Prozent das Volumen des Körpers ABCDEF größer ist als das Volumen des Körpers ABCDE, ohne für diese Volumina konkrete Werte zu berechnen.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1
1. Schritt: Rechten Winkel nachweisen
Ein rechter Winkel zwischen zwei Vektoren liegt vor, wenn das Skalarprodukt ergibt.
ergibt.


 2. Schritt: Flächeninhalt berechnen
2. Schritt: Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=& 10^2+10\cdot\mid\overline{CE}\mid+10\cdot6 & \quad \scriptsize \\[5pt]
&\approx& 277 & \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/151e9f52fefdd6d28ab6d23578cae6ae40d4a6189390da98cd9d036b6a385a48?color=5a5a5a)
Der Flächeninhalt beträgt cm
cm .
.
Ein rechter Winkel zwischen zwei Vektoren liegt vor, wenn das Skalarprodukt
Der Flächeninhalt beträgt
2.2
1. Schritt: Parametergleichung der Ebene  aufstellen.
aufstellen.
2. Schritt: Gleichungen aus der Paramatergleichung ablesen.
3. Schritt: Koordinatenform berechnen.
Damit hat die Ebene die Koordinatenform:
die Koordinatenform: 
2. Schritt: Gleichungen aus der Paramatergleichung ablesen.
3. Schritt: Koordinatenform berechnen.
Damit hat die Ebene
2.3
2.4
Sei  der Punkt, der auf
der Punkt, der auf  liegt.
liegt.
Der Körper ist symmetrisch entlang der Strecke . Die Länge der gesuchten Linie ist somit
. Die Länge der gesuchten Linie ist somit  .
.
Die gesuchte Linie soll möglichst kurz sein. Deshalb muss das Skalarprodukt gleich
gleich  sein, damit die Strecke
sein, damit die Strecke  senkrecht zu
senkrecht zu  liegt.
liegt.
Der Körper ist symmetrisch entlang der Strecke
Die gesuchte Linie soll möglichst kurz sein. Deshalb muss das Skalarprodukt
2.5.1

2.5.2
1. Schritt: Volumen des Körpers  .
.
Beim Körper handelt es sich um eine Pyramide. Das Volumen einer Pyramide entspricht
handelt es sich um eine Pyramide. Das Volumen einer Pyramide entspricht  mal Grundfläche mal Höhe. Also gilt:
mal Grundfläche mal Höhe. Also gilt:
 2. Schritt: Volumen des Körpers
2. Schritt: Volumen des Körpers  .
.
Beim Körper handelt es sich um einen (diagonal) halbierten Quader. Also gilt:
handelt es sich um einen (diagonal) halbierten Quader. Also gilt: ![\(\begin{array}[t]{rll}
V_{ABCDEF}&=&\frac{1}{2}\cdot\mid\overline{AB}\mid^2\cdot \mid\overline{DE}\mid{}& \quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/39098f091b4b5d5bcb21a6572a141d158f47c6deb2f5cff82035db5afcc4bb74?color=5a5a5a) 3. Schritt: Größenunterschied bestimmen.
3. Schritt: Größenunterschied bestimmen.
Somit ist das Volumen um
um  größer als das Volumen von
größer als das Volumen von  .
.
Beim Körper
Beim Körper
Somit ist das Volumen