Pflichtaufgaben
1 Analysis
Gegeben ist die in
1.1
Begründe, dass der Graph von 
symmetrisch bezüglich des Koordinatenursprungs ist.
(1 BE)
1.2
Der Graph von und die 
-Achse schließen eine Fläche ein, die aus zwei Teilflächen besteht. Berechne den Inhalt der gesamten Fläche.
(4 BE)
2 Analytische Geometrie
Gegeben sind die Vektoren
2.1
Überprüfe, ob 
und 
senkrecht zueinander sind.
(2 BE)
2.2
Gegeben ist der Vektor 
mit 
Vergleiche die Längen der Vektoren und 
Vergleiche die Längen der Vektoren
(3 BE)
3 Stochastik
In einer Urne befinden sich 5 gelbe Kugeln und 3 blaue Kugeln. Es werden nacheinander zwei Kugeln ohne Zurücklegen aus der Urne gezogen und ihre Farbe wird notiert.
3.1
Die Abbildung zeigt ein unvollständig beschriftetes Baumdiagramm für das beschriebene Zufallsexperiment.
Vervollständige das abgebildete Baumdiagramm.
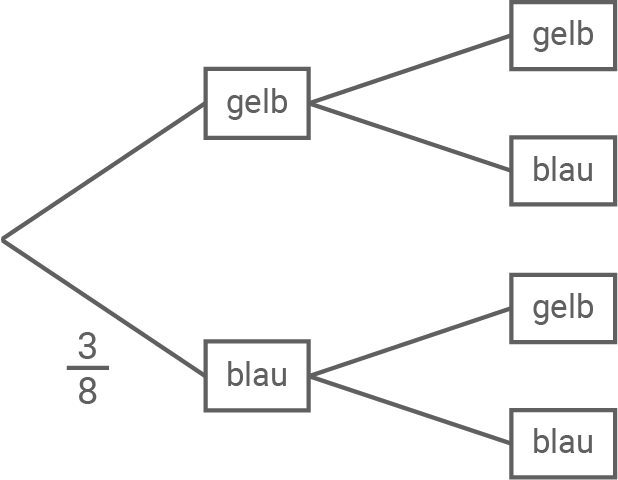
Vervollständige das abgebildete Baumdiagramm.
(2 BE)
3.2
Berechne die Wahrscheinlichkeit dafür, dass genau eine gelbe Kugel gezogen wird.
(2 BE)
3.3
Formuliere das Gegenereignis zum Ereignis: „Es werden zwei gelbe Kugeln gezogen.“
(1 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?1 Analysis
1.1
Der Graph von ist symmetrisch bezüglich des Koordinatenursprungs, da 
ein Polynom ist, welches nur ungerade Potenzen von enthält.
1.2
1. Schritt: Nullstellen bestimmen
![\(\begin{array}[t]{rll}
f(x)&=&0 \\[5pt]
x^3-4x&=&0 \\[5pt]
x\cdot(x^2-4)&=&0
\end{array}\)](https://mathjax.schullv.de/2a71bc9752b2f7a5911df9ad2dca78f17e2fb9e025e20e8f7b5ef62f01988914?color=5a5a5a)
Mit dem Satz vom Nullprodukt folgt 
und weiter:
![\(\begin{array}[t]{rll}
x^2-4&=&0 &\quad \scriptsize \mid\;+4\\[5pt]
x^2&=&4 &\quad \scriptsize \mid\;\sqrt{\;}\\[5pt]
x_{2;3}&=&\pm2
\end{array}\)](https://mathjax.schullv.de/c785006fde31f76488cba8c0689712e0755bf62fc5b37d7b473a5b9722dd3ba8?color=5a5a5a)
2. Schritt: Flächeninhalt berechnen
Die beiden Flächenstücke, aus denen die Fläche besteht, sind gleich groß, da nach Aufgabenteil a) punktsymmetrisch zum Urpsrung ist und eine der drei Nullstellen ist. Somit folgt für den gesuchten Flächeninhalt 
![\(\begin{array}[t]{rll}
A&=&2\cdot\displaystyle\int_{-2}^{0}f(x)\;\mathrm dx \\[5pt]
&=&2\cdot\left[\dfrac{1}{4} x^4-2 x^2\right]_{-2}^0 \\[5pt]
&=&2\cdot(0-(4-8)) \\[5pt]
&=&8\;[\text{FE}]
\end{array}\)](https://mathjax.schullv.de/a5f3ddc9bcd576a46357b9eaf286d55901ac6a817e6b8e0905ee6978cd1415d8?color=5a5a5a)
2 Analytische Geometrie
2.1
2.2
Für den Vektor folgt:
![\(\begin{array}[t]{rll}
\overrightarrow{c}&=&\overrightarrow{a}+\overrightarrow{b} \\[5pt]
&=&\pmatrix{-3\\2\\6}+\pmatrix{4\\-3\\-5} \\[5pt]
&=&\pmatrix{1\\-1\\1}
\end{array}\)](https://mathjax.schullv.de/aed99d3fe755b22521a172e10e4e57bf7946549194eaa394ecf84b0f79809ea1?color=5a5a5a)
Für die Längen der Vektoren und ergibt sich damit:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{a}\right\vert&=&\left\vert\pmatrix{-3\\2\\6}\right\vert \\[5pt]
&=&\sqrt{(-3)^2+2^2+6^2} \\[5pt]
&=&\sqrt{49} \\[5pt]
&=&7
\end{array}\)](https://mathjax.schullv.de/e4353f77050e0d5f1d436263406484ce95e36b76cf78f180fae92f15be93f128?color=5a5a5a)
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{c}\right\vert&=&\left\vert\pmatrix{1\\-1\\1}\right\vert \\[5pt]
&=&\sqrt{1^2+(-1)^2+1^2} \\[5pt]
&=&\sqrt{3}
\end{array}\)](https://mathjax.schullv.de/165cd2a226da7bf3848c52c35062755790e2a64aaaa64242c7aefd2f2b7f553d?color=5a5a5a)
Somit gilt 
3 Stochastik
3.1
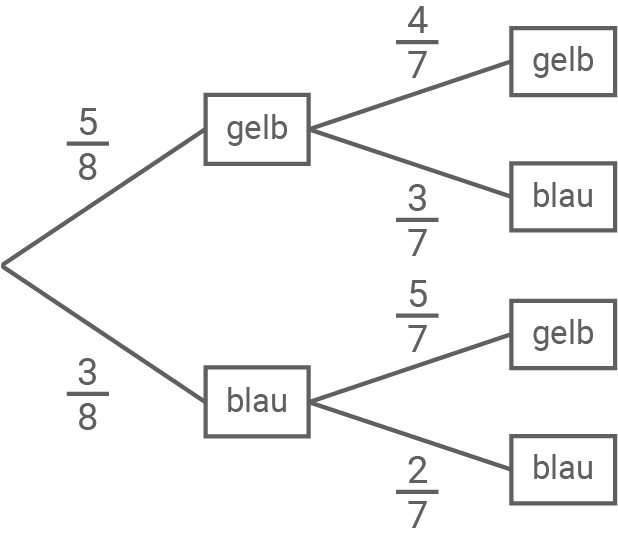
3.2
3.3
„Es wird mindestens eine blaue Kugel gezogen“