Wahlteil A1

A1 Analysis

Gegeben ist die Funktion $m$ mit $m(x)=\sin\left(\frac{\pi}{50}\cdot x\right)+2$ und $x\in\mathbb{R}.$ Ihr Graph heißt $G.$

1.1

Bestimme den Funktionswert von $m$ an der Stelle $x=175.$

Berechne die Koordinaten der lokalen Extrempunkte von $G$ im Intervall $0\leq x\leq 100.$
Weise die Art der Extrema nach.

Begründe ohne weitere Rechnungen, dass $m$ keine Nullstellen besitzt.
Ermittle alle Stellen, an denen $G$ den maximalen Anstieg besitzt.
Zeichne $G$ im Interval $0\leq x \leq 200$ in ein Koordinatensystem.

(15 BE)

1.2

Der Graph $G,$ die Koordinatenachsen und die Gerade $x=50$ begrenzen eine Fläche $A$ vollständig.
Berechne den Inhalt von $A.$

Es gibt eine Ursprungsgerade, die $A$ halbiert.
Ermittle die Stelle, an der diese Ursprungsgerade den Graphen $G$ schneidet.

(6 BE)

1.3

Das Räuber-Beute-Modell ist eine vereinfachte Veranschaulichung von Populationsschwankungen einer Räuberpopulation in Abhängigkeit von einer Beutepopulation.
Die Entwicklung einer Population von Marienkäfern wird durch die Funktion $m$ beschrieben. Eine Blattlauspopulation stellt die Beute dieser Marienkäferpopulation dar.
Die Entwicklung der Blattlauspopulation wird durch die Funktion $b$ beschrieben:

$b(x)=5 \cdot \sin \left(\frac{\pi}{50}\cdot (x+25)\right)+6$

Dabei entspricht $x$ der Zeit in Tagen mit $0\leq x \leq 200.$ Die Funktionswerte von $m$ und $b$ geben die jeweilige Populationsgröße in $10\,000$ Tieren an.

1.3.1

Markiere in der Abbildung diejenigen Zeitintervalle, in denen die Blattlauspopulation abnimmt.

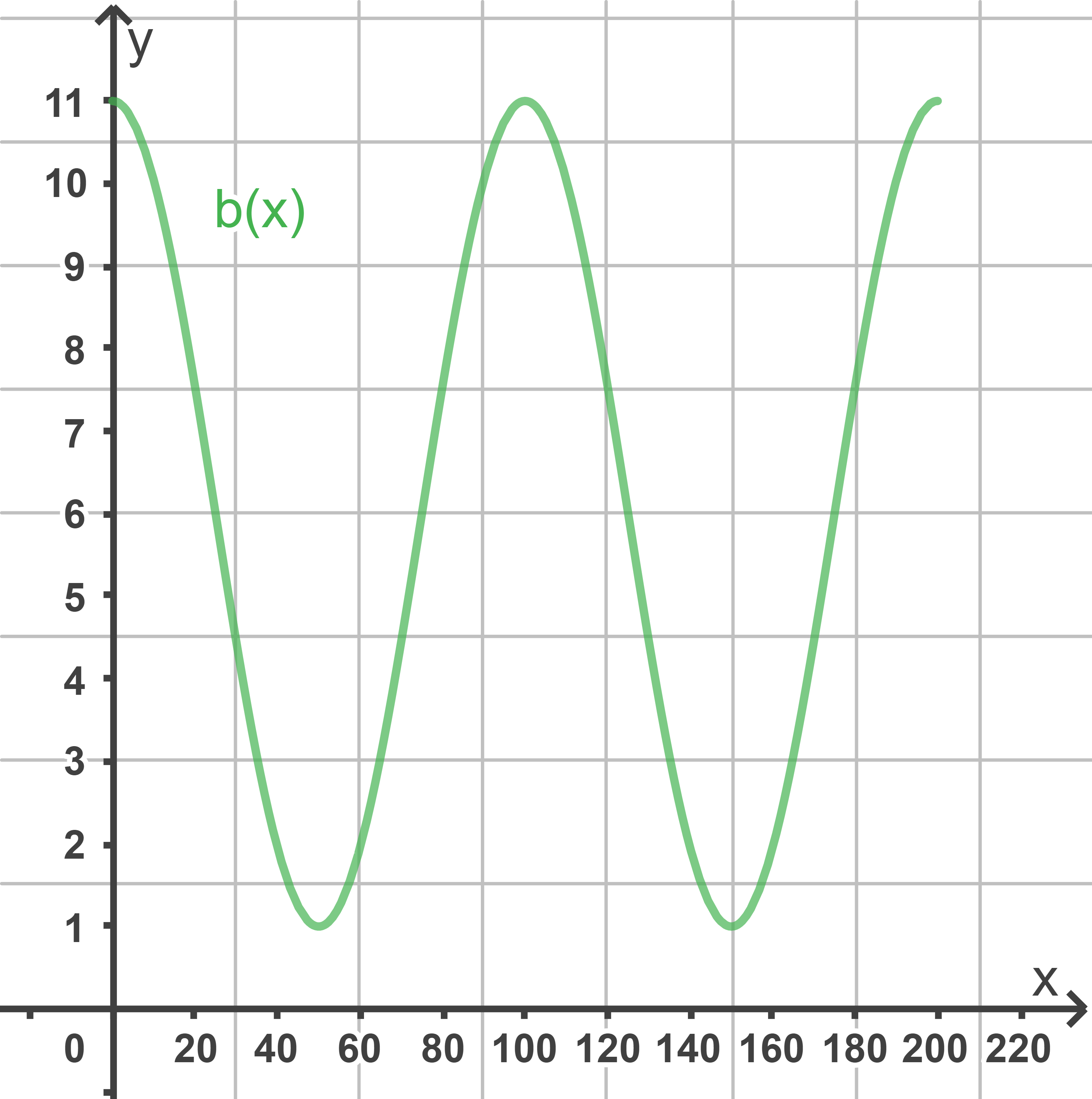
Graph einer Funktion b(x) im Koordinatensystem mit x- und y-Achse.

(2 BE)

1.3.2

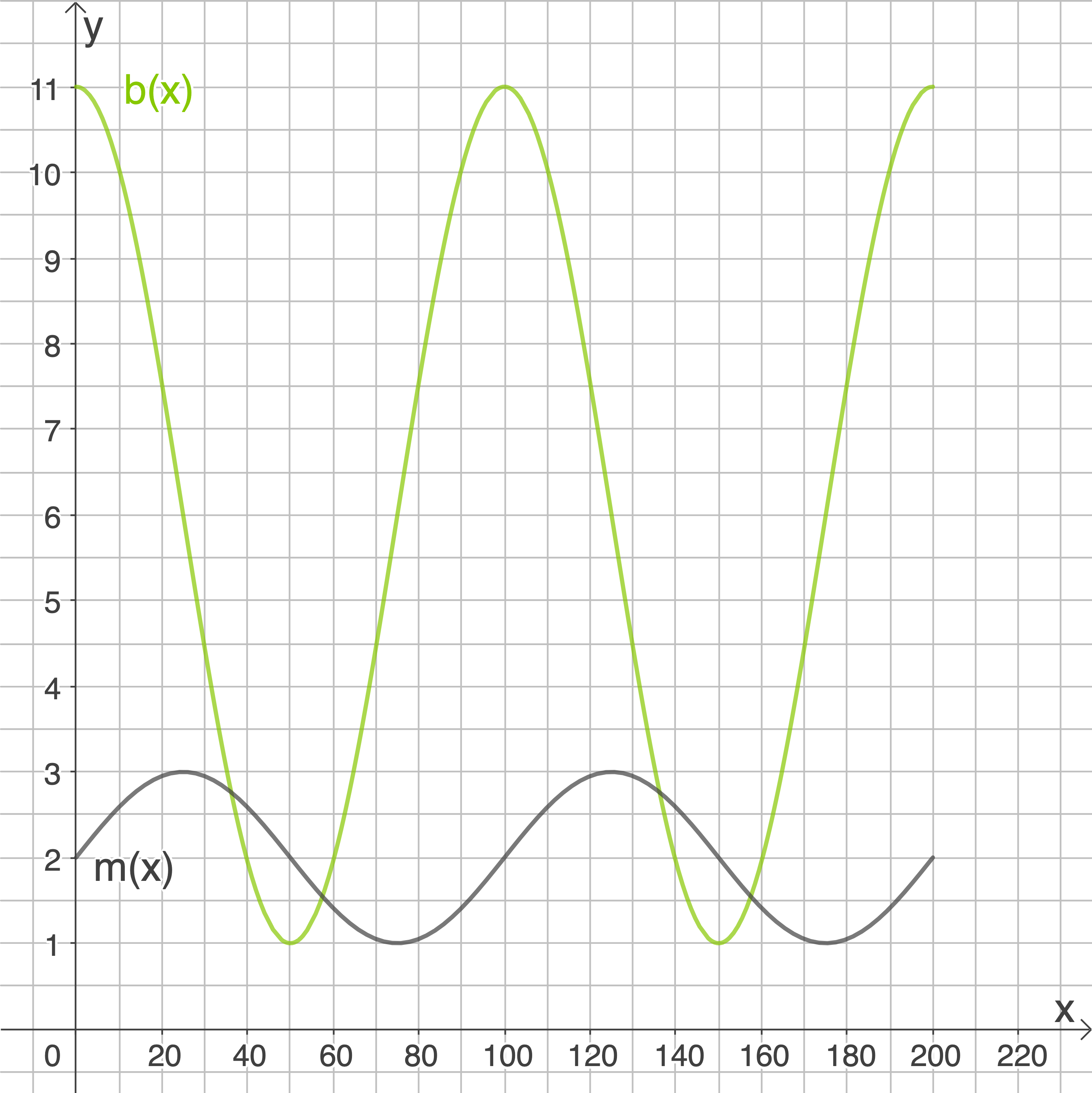
Berechne und vergleiche die Populationsgrößen zum Zeitpunkt $x=30.$

(3 BE)

1.3.3

Berechne das Zeitintervall im Zeitraum $0\leq x \leq 100,$ in dem sowohl die Marienkäferpopulation als auch die Blattlauspopulation abnimmt.

(5 BE)

1.3.4

Vergleiche die mittleren Änderungsraten der Populationen im Zeitraum $80 \leq x \leq 100.$
Interpretiere das Ergebnis im Sachzusammenhang.

(4 BE)

1.1

$m(175)=1$

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

Ableitungen:

$\(m$

Bestimme das notwendige Kriterium für Extrema mit der Solve-Funktion deines CAS Taschenrechners:

$\(m$ (im Intervall $0\leq x\leq 100$ )

Bestimme das hinreichende Kriterium für Extrema mit der Solve-Funktion deines CAS Taschenrechners:
$\(m$ lok. Maximum
$\(m$ lok. Minimum

Koordinaten:

$m(x_1)=3 \,;\;HP\left(25 \mid 3 \right)$

$m(x_2)=1 \,;\;TP\left(75 \mid 1 \right)$

$m$ ist eine verschobene Sinusfunktion, bei der lokale Extrema auch globale Extrema sind. Da das lokale Minimum $1$ größer als $0$ ist, gibt es keine Nullstelle.

(Verschobene) Sinusfunktionen besitzen den maximalen Anstieg eine Viertelperiode vor den lokalen Hochpunkten.
Die Periode von $m$ ist:

$p= \dfrac{2\pi}{\dfrac{\pi}{50}}=100,$ also sind die Stellen des maximalen Anstiegs:
$x=25-\dfrac{100}{4}+100k=100k, \, k \in\mathbb{Z}$

Grafik mit zwei Kurven, b(x) in grün und m(x) in grau, auf einem Koordinatensystem.

1.2

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$A= \,\bigg\vert \, \displaystyle\int_{0}^{50}m(x) \mathrm dx \,\bigg \vert \, =100+\dfrac{100}{\pi}$

$x_0$ sei die gesuchte Stelle. Die rechte Teilfläche von $A$ besteht dann aus einem rechtwinkligen Dreieck mit den Kathetenlängen $x_0$ und $m(x_0)$ sowie aus der Fläche unter $m$ im Intervall $\leq x \leq 50.$
Also gilt:
$\dfrac{1}{2}\cdot x_0 \cdot m(x_0)+ \displaystyle\int_{x_0}^{50}m(x) \mathrm dx = \dfrac{A}{2} \rightarrow x_0 \approx 43,7$

1.3.1

Diagramm mit zwei Kurven, einer grünen b(x) und einer schwarzen m(x), in einem Koordinatensystem.

1.3.2

$10000 \cdot m(30) \approx 29511$

$10000 \cdot b(30) \approx44549$

Es leben ca. $1,5$ mal mehr Blattläuse als Marienkäfer.

1.3.3

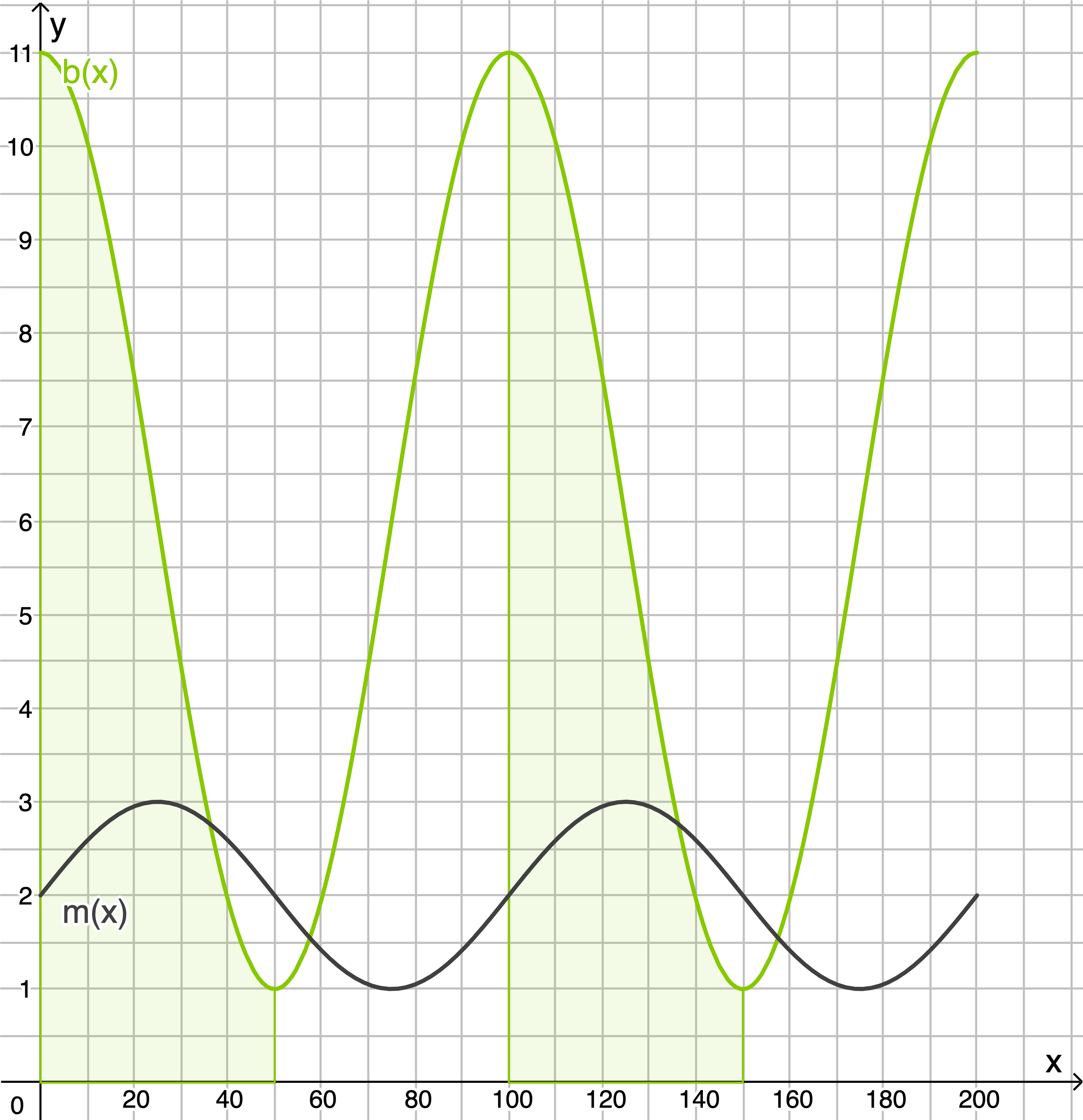
Der Zeitraum, in dem die Blattlauspopulation abnimmt, ist schon aus 1.3.1 als $0\leq x\leq 50$ bekannt.
Die Marienkäferpopulation nimmt vom HP zum TP ab, also im Intervall $25 \leq x \leq 75$ (siehe 1.1).
Folglich nehmen beide Populationen im Intervall $25\leq x\leq 50$ ab.

1.3.4

$10000 \cdot \dfrac{m(100)-m(80)}{100-80} \approx 476\lt 1727 \approx 10000 \cdot \dfrac{b(100-b(80)}{100-80}$

Also wächst die Marienkäferpopulation in diesem Zeitraum durchschnittlich langsamer als die Blattlauspopulation.