Wahlteil A2

A2 Analytische Geometrie

$ABCD$ ist die Grundfläche eines geraden Prismas $ABCDEFGH$ mit der Kante $AE.$

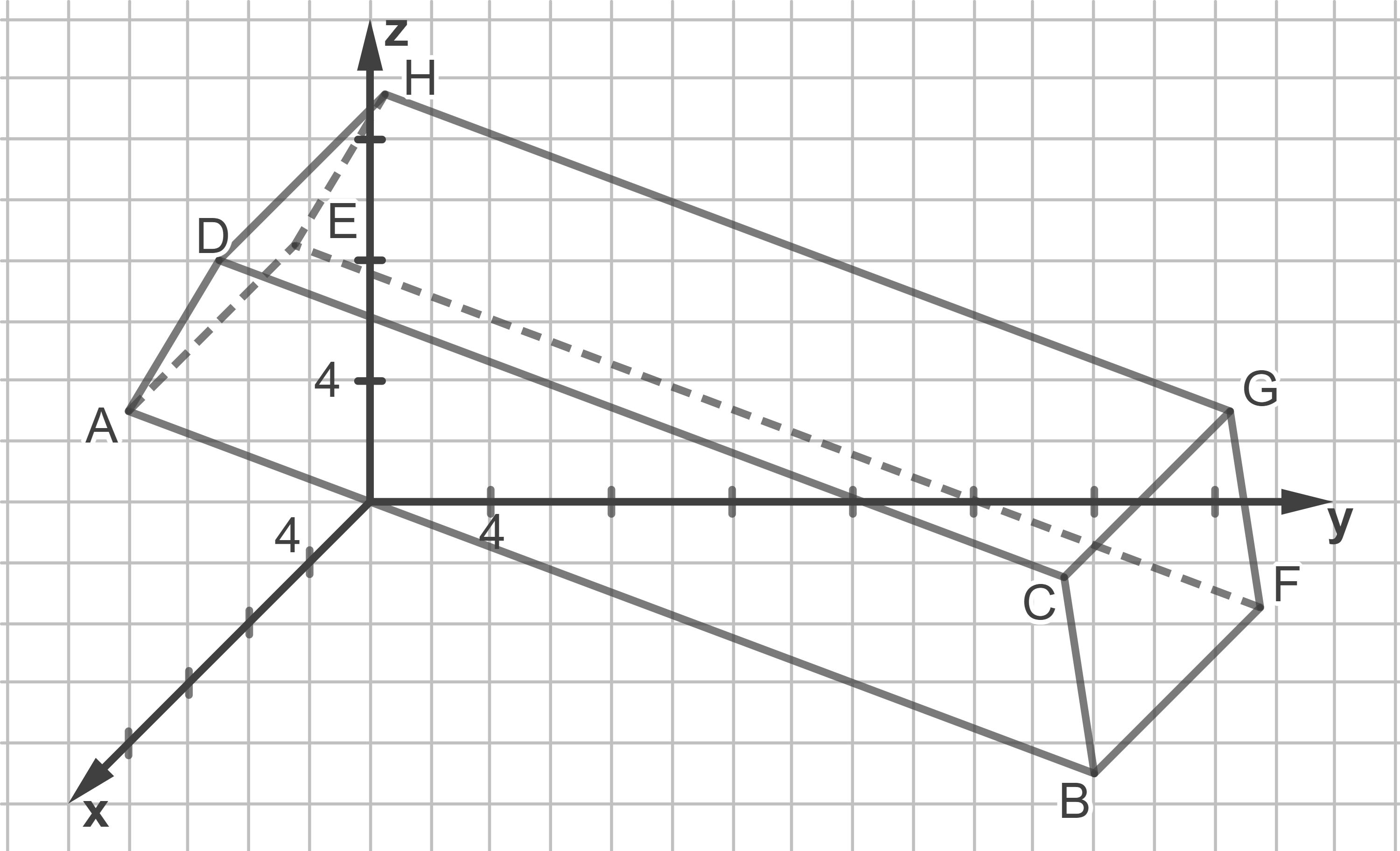
3D-Diagramm eines Quaders mit Achsenbeschriftung und Maßen.

Bekannt sind die Koordinaten der Eckpunkte $A (0 \mid -8 \mid 3),$ $B (0 \mid 24\mid -9),$ $C (0\mid 23 \mid -2,5 ),$ $D (0\mid -5\mid 8),$ $E (-11\mid -8\mid 3)$ und $G(-11\mid 23\mid -2,5).$

2.1

Ermittle die Koordinaten der Punkte $F$ und $H.$

Bestimme eine Koordinatengleichung für die Ebene, in der die Seitenfläche $ABFE$ liegt.

(6 BE)

2.2

Zeige rechnerisch, dass die Grundfläche des Prismas die Form eines Trapezes hat und dieses Trapez nicht gleichschenklig ist.

(5 BE)

2.3

Begründe ohne Rechnung, dass das Skalarprodukt der Kantenvektoren $\overrightarrow{DA}$ und $\overrightarrow{DH}$ null ist.

(2 BE)

2.4

Weise nach, dass die Gerade $AB$ durch den Koordinatenursprung verläuft.

(3 BE)

An einem Fjord in Südnorwegen wurde als Unterwasserrestaurant ein Gebäude errichtet, dessen Form stark vereinfacht durch das Prisma $ABCDEFGH$ modelliert werden kann.

Die $xy$ -Ebene des Koordinatensystems stellt dabei die Meeresoberfläche bei mittlerem Wasserstand dar.
Im Koordinatensystem entspricht eine Längeneinheit einem Meter.
Die Dicken aller Wände und Fenster werden vernachlässigt.

2.5

Ein großes rechteckiges Panoramafenster aus stabilem Acrylglas gewährt Einblick in die Unterwasserwelt. Seine Eckpunkte sind im Modell die Punkte $C$ und $G$ sowie die Mittelpunkte der Kanten $BC$ und $FG.$

Berechne die Materialkosten für das Panoramafenster, wenn $1\,\text{m}^2$ des speziellen Acrylglases $20\,000\,\,€$ kostet.

(5 BE)

2.6

An den Innenwänden des Gebäudes wurde der mittlere Wasserstand durch eine umlaufende Linie markiert.
Ermittle die Gesamtlänge der Markierung.
Ermittle das Volumen für den Gebäudeteil, der sich unterhalb der Markierung befindet.

(11 BE)

2.7

Der Neigungswinkel zwischen der Seitenfläche $ABFE$ und der $xy$ -Ebene entspricht etwa der Hangneigung der Fjordwand zur Meeresoberfläche.

Berechne die Hangneigung.

(3 BE)