Wahlaufgaben
4 Analysis
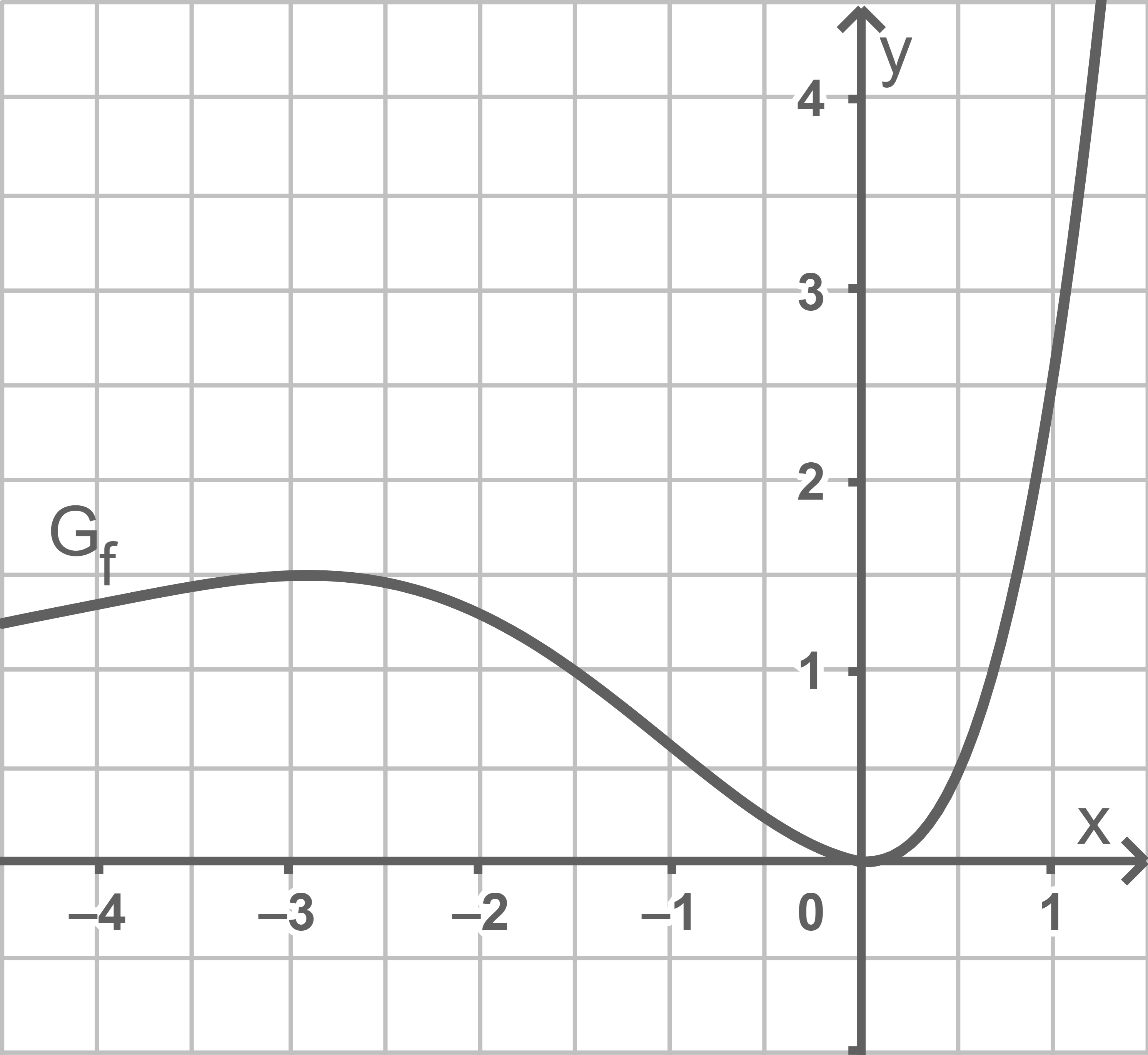
Die Abbildung zeigt den Graphen  einer in
einer in  definierten Funktion
definierten Funktion 
4.1
Bestimme grafisch den Wert des Integrals 
(2 BE)
4.2
Beschreibe, wie der Graph der in  definierten Funktion
definierten Funktion  mit
mit  aus
aus  erzeugt werden kann.
erzeugt werden kann.
Gib die Koordinaten des Hochpunkts des Graphen von an.
an.
Gib die Koordinaten des Hochpunkts des Graphen von
(3 BE)
5 Analytische Geometrie
Gegeben sind die Punkte
5.1
Entscheide, ob es einen Wert von  gibt, für den die Gerade
gibt, für den die Gerade  parallel zur
parallel zur  -Ebene verläuft.
-Ebene verläuft.
Begründe deine Entscheidung.
Begründe deine Entscheidung.
(2 BE)
5.2
Der Koordinatenursprung sowie die Punkte  und
und  bilden ein Dreieck.
bilden ein Dreieck.
Ermittle diejenigen Werte von für die das Dreieck in
für die das Dreieck in  einen rechten Winkel hat.
einen rechten Winkel hat.
Ermittle diejenigen Werte von
(3 BE)
6 Stochastik
Eine Ärztin verordnet ihrer Patientin zwei Medikamente, deren Anwendung unabhängig voneinander zu Nebenwirkungen führen kann. Bei der Anwendung des ersten Medikaments treten in
Die Anwendung des ersten Medikaments führt zu Nebenwirkungen.
Die Anwendung des zweiten Medikaments führt zu Nebenwirkungen.
6.1
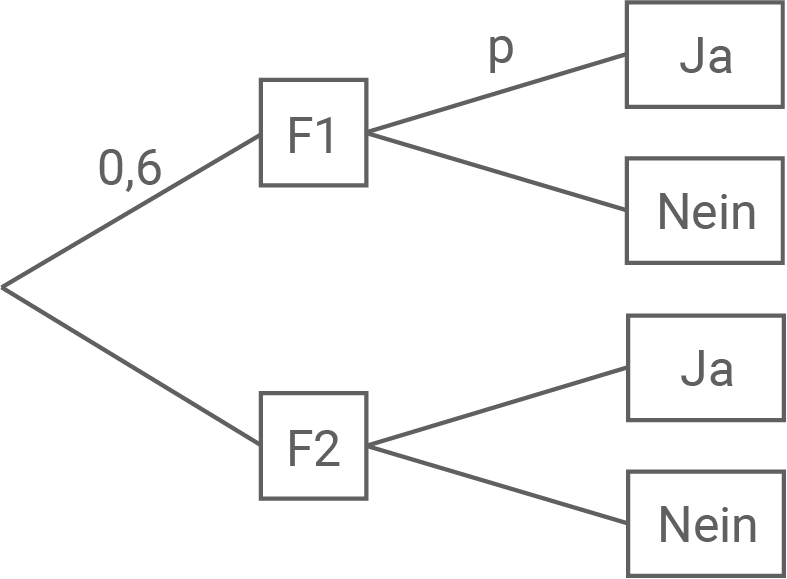
Dieser Sachverhalt kann in einer Vierfeldertafel dargestellt werden.
Begründe, dass gilt, und ergänze die fehlenden Werte in der abgebildeten Vierfeldertafel.
gilt, und ergänze die fehlenden Werte in der abgebildeten Vierfeldertafel.
Begründe, dass
(3 BE)
6.2
Bestimme die Wahrscheinlichkeit dafür, dass höchstens eines der beiden Medikamente zu Nebenwirkungen führt.
(2 BE)
7 Analysis
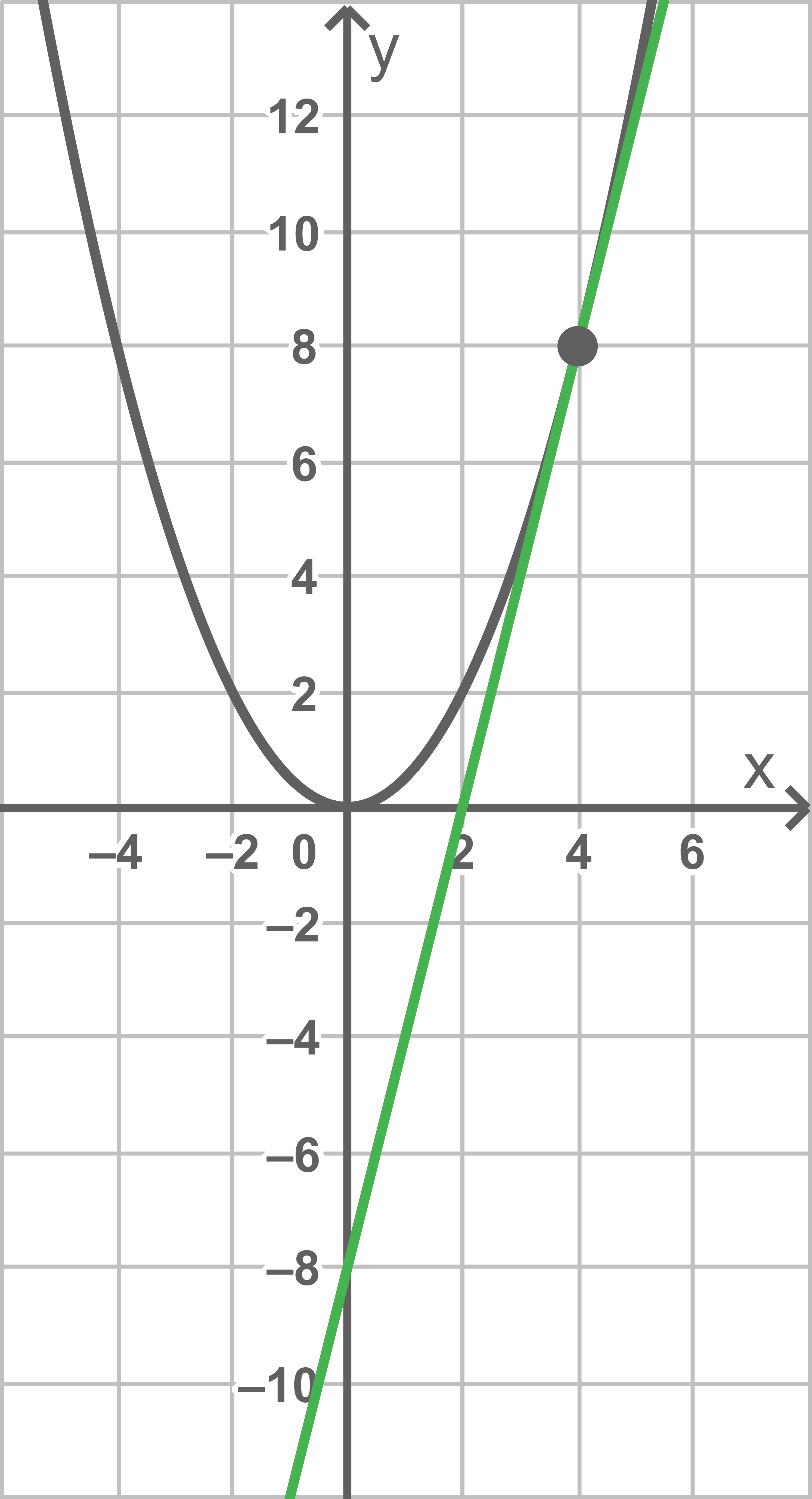
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von  sowie die Tangente
sowie die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt 

7.1
Gib anhand der Abbildung eine Gleichung der Tangente  an.
an.
(1 BE)
7.2
Weise nach, dass für jeden Wert  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse im Punkt
-Achse im Punkt  schneidet.
schneidet.
(4 BE)
8 Analytische Geometrie
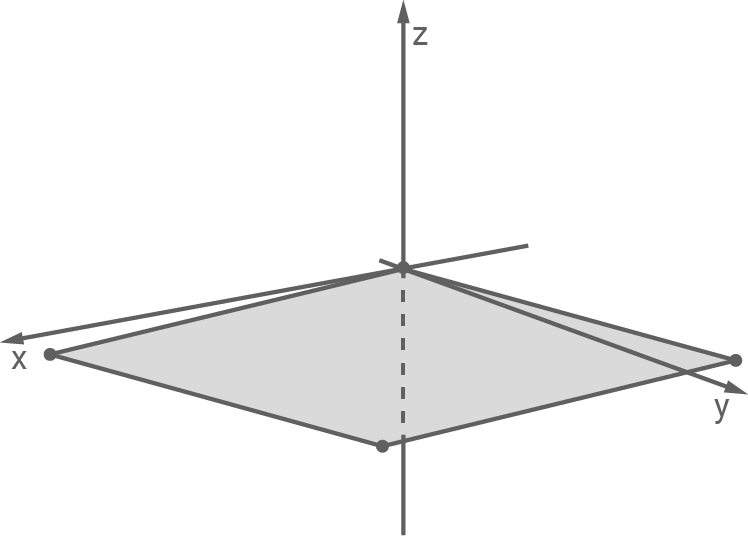
Betrachtet wird das Quadrat, das die folgenden Eigenschaften besitzt:- Das Quadrat liegt in der
-Ebene.
- Ein Eckpunkt liegt im Koordinatenursprung.
- Der Schnittpunkt der Diagonalen des Quadrats liegt auf der Gerade
mit
(5 BE)
9 Stochastik
Um Jugendliche bei einer Befragung zum sensiblen Thema „Nicht erledigte Hausaufgaben“ dazu zu bewegen, die ihnen gestellte Frage wahrheitsgemäß zu beantworten, wird folgendes Verfahren angewandt: Von den an der Befragung teilnehmenden Jugendlichen erhalten
F1:
„Ist es wahr, dass du in den letzten zwei Wochen mindestens einmal die Hausaufgaben nicht erledigt hast?“
F2:
„Ist es wahr, dass du in den letzten zwei Wochen alle Hausaufgaben erledigt hast?“
Nur der befragten Person selbst ist bekannt, welche der beiden Fragen sie erhalten hat. Sie beantwortet die Frage wahrheitsgemäß mit „Ja“ bzw. mit „Nein“.
Es kann davon ausgegangen werden, dass der Anteil der Befragten, die in den letzten zwei Wochen mindestens einmal die Hausaufgaben nicht erledigt haben, unter denjenigen, die die Frage F1 erhielten, ebenso groß ist wie unter allen Befragten. Dieser Anteil wird mit
9.1
Vervollständige das abgebildete Baumdiagramm, so dass es das beschriebene Verfahren darstellt.
(2 BE)
9.2
Es werden 1000 Jugendliche befragt. Von diesen antworten 420 mit „Ja“.
Berechne den Anteil der sich auf Grundlage dieses Ergebnisses ergibt.
der sich auf Grundlage dieses Ergebnisses ergibt.
Berechne den Anteil
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?4 Analysis
4.1
Der Wert des Integrals gibt den Inhalt der Fläche zwischen dem Graphen und der  -Achse zwischen den beiden Grenzen an. Im betrachteten Bereich sind das ungefähr 8 Kästchen, das heißt der Wert des Integrals ist etwa
-Achse zwischen den beiden Grenzen an. Im betrachteten Bereich sind das ungefähr 8 Kästchen, das heißt der Wert des Integrals ist etwa ![\(8\cdot0,5^2=2\;[\text{FE}].\)](https://mathjax.schullv.de/f52af0e22124d1ded4d66412fc64dfb022b2971fc07ebf226bf4f3e0663bc090?color=5a5a5a)
4.2
Erzeugung des Graphen beschreiben
Der Graph von  kann aus
kann aus  durch Spiegelung an der
durch Spiegelung an der  -Achse und anschließende Verschiebung um
-Achse und anschließende Verschiebung um  in
in  -Richtung erzeugt werden
Koordinaten des Hochpunkts angeben
Durch die Spiegelung an der
-Richtung erzeugt werden
Koordinaten des Hochpunkts angeben
Durch die Spiegelung an der  -Achse wird aus dem Tiefpunkt von
-Achse wird aus dem Tiefpunkt von  ein Hochpunkt. Die anschließende Verschiebung liefert somit die Koordinaten
ein Hochpunkt. Die anschließende Verschiebung liefert somit die Koordinaten  für den Hochpunkt des Graphen von
für den Hochpunkt des Graphen von 
5 Analytische Geometrie
5.1
Damit die Gerade  parallel zur
parallel zur  -Ebene verläuft, müssen alle Punkte auf dieser die gleiche
-Ebene verläuft, müssen alle Punkte auf dieser die gleiche  Koordinate besitzen. Da die
Koordinate besitzen. Da die  -Koordinaten von
-Koordinaten von  und
und  verschieden sind, existiert kein solches
verschieden sind, existiert kein solches 
5.2
6 Stochastik
6.1
6.2
7 Analysis
7.1
Die Tangente  gegeben durch die Gleichung
gegeben durch die Gleichung  hat eine positive Steigung, einen
hat eine positive Steigung, einen  -Achsenabschnitt von
-Achsenabschnitt von  und schneidet die
und schneidet die  -Achse bei
-Achse bei  Für die Steigung
Für die Steigung  folgt somit:
folgt somit:
 Somit ergibt sich die Gleichung
Somit ergibt sich die Gleichung 
7.2
Die allgemeine Gleichung der Tangente ist gegeben durch  Für die Ableitung von
Für die Ableitung von  gilt:
gilt:
 Somit folgt
Somit folgt  und
und  Einsetzen der Koordinaten des Punktes
Einsetzen der Koordinaten des Punktes  an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
![\(\begin{array}[t]{rll}
\dfrac{1}{2}u^2&=& u\cdot u + n &\quad \scriptsize \mid\;-u^2 \\[5pt]
-\dfrac{1}{2}u^2&=& n
\end{array}\)](https://mathjax.schullv.de/745371ef619f158f2bb45bd90fac7ecb2e03caa7223013b072f1e6c0dc28b526?color=5a5a5a) Somit gilt
Somit gilt  und die Tangente schneidet die
und die Tangente schneidet die  -Achse damit im Punkt
-Achse damit im Punkt 
8 Analytische Geometrie
Der Schnittpunkt der Geraden  mit der
mit der  -Ebene, in der das Quadrat liegt, wird durch den Wert von
-Ebene, in der das Quadrat liegt, wird durch den Wert von  bestimmt, der aus
bestimmt, der aus  folgt. Diese Gleichung ergibt
folgt. Diese Gleichung ergibt  Somit ergibt sich für den Ortsvektor des Schnittpunkts der Diagonalen:
Somit ergibt sich für den Ortsvektor des Schnittpunkts der Diagonalen:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=&\pmatrix{-1\\4\\-2}+2\cdot\pmatrix{2\\0\\1} \\[5pt]
&=&\pmatrix{3\\4\\0}
\end{array}\)](https://mathjax.schullv.de/8a43bf46838230053070dbae759a306149a517c19ffc49ae46d6fde41468bd75?color=5a5a5a) Die beiden Diagonalen teilen das Dreieck in vier rechtwinklige Dreiecke mit gleichem Flächeninhalt, deren an den rechten Winkel anliegende Seiten die Länge
Die beiden Diagonalen teilen das Dreieck in vier rechtwinklige Dreiecke mit gleichem Flächeninhalt, deren an den rechten Winkel anliegende Seiten die Länge ![\(\left\vert\overrightarrow{OS}\right\vert=\sqrt{3^2+4^2}=5\;[\text{LE}]\)](https://mathjax.schullv.de/e8d62675d741e76c17f3573946588478b3e985c5ef837fbca18d79bc9f6bac78?color=5a5a5a) besitzen. Somit folgt für den Flächeninhalt
besitzen. Somit folgt für den Flächeninhalt  des gesamten Quadrats:
des gesamten Quadrats:
![\(\begin{array}[t]{rll}
A&=&4\cdot\dfrac{1}{2}\cdot5^2 \\[5pt]
&=&2\cdot25 \\[5pt]
&=&50\;[\text{FE}]
\end{array}\)](https://mathjax.schullv.de/d50359f8286654aba67fd29b70ac588e9003c86c8a916c77137e8a8219470022?color=5a5a5a)
9 Stochastik
9.1
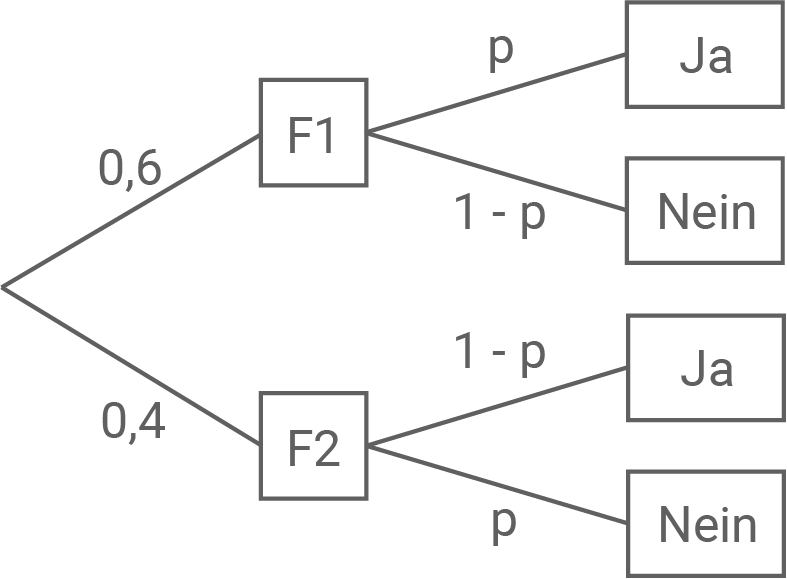
9.2