Analysis

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f_t$ mit $f_t(x)=\left(x^2-2x\right)\cdot \left(x-t\right)$ und $t\in\mathbb{R}.$

1.1

Begründe, dass $0$ und $2$ sowie $t$ die Nullstellen von $f_t$ sind.

(1 BE)

1.2

Zeichne den Graph von $f_3$ in ein Koordinatensystem.

(2 BE)

1.3

Jeder Graph von $f_t$ besitzt im Ursprung eine Tangente.
Ermittle den Wert von $t$ so, dass diese Tangente den Anstieg $22$ besitzt.

(2 BE)

1.4

Berechne den Inhalt der Flächen, die der Graph von $f_5$ mit der $x$ -Achse einschließt.

(3 BE)

1.5

Für jeden Wert von $t$ wird durch den Graphen von $f_t$ mindestens eine Fläche mit der $x$ -Achse eingeschlossen.
Gib alle Werte von $t$ mit $t\gt 0$ an, sodass der Inhalt der oberhalb der $x$ -Achse liegenden Fläche gleich dem Inhalt der unterhalb der $x$ -Achse liegenden Fläche ist.

(2 BE)

Gegeben ist die Funktion $f$ der Gleichung $f(x)=\left(20x^2+x\right)\cdot \mathrm e^{-2x}+0,3$ und $x\in\mathbb{R}.$
Der Graph von $f$ heißt $G.$

2.1

Gib die Koordinaten des Schnittpunktes von $G$ mit der $y$ -Achse an.
Ermittle rechnerisch Koordinaten und Art der Extrempunkte von $G.$
Der Graph $G$ hat zwei Wendepunkte. Bestimme deren Koordinaten.

(6 BE)

2.2

Zeichne $G$ im Intervall $0\leq x\leq 5.$

(2 BE)

2.3

Der horizontal verlaufende Erdboden eines Spielplatzes wird in einem Koordinatensystem durch die Abszissenachse dargestellt. Eine Rutsche auf diesem Spielplatz, bestehend aus einer Leiter und einer Rutschbahn, ist auf beiden Seiten ebenflächig bis zum Erdboden verkleidet (siehe Abbildung). Die obere Begrenzungslinie der Verkleidung dient als Handlauf und wird durch den Graphen der Funktion $f$ im Intervall $0\leq x\leq 5$ dargestellt. Eine Verankerung der Rutsche befindet sich im Punkt $A,$ der im Modell dem Koordinatenursprung entspricht.
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

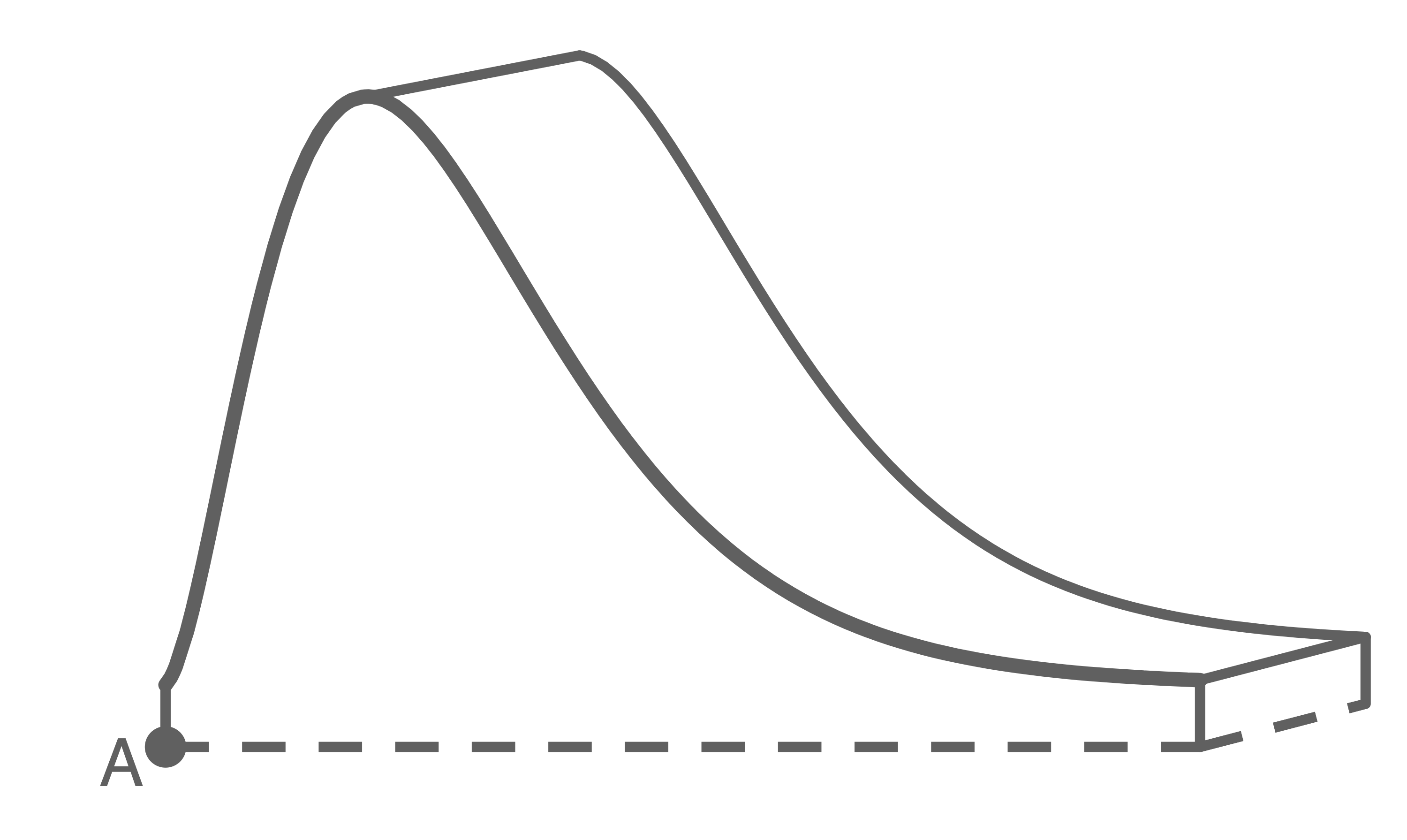
2.3.1

Bestimme für das Ende der Rutsche die Höhe des Handlaufs über dem Erdboden.

(1 BE)

2.3.2

Die beiden seitlichen Kanten der aus Edelstahl bestehenden Verkleidung stehen senkrecht zum Erdboden. Ein Quadratmeter Edelstahl kostet 202,20 €.
Berechne die Kosten für die Verkleidung auf beiden Seiten der Rutsche.

(4 BE)

$\,$

Das Logo des Herstellers der Rutsche hat die Form eines Dreiecks. Das möglichst große Logo soll auf einer dieser verkleideten Flächen aufgebracht werden. Für die Planung werden die Eckpunkte des Logos mit $A(0\mid 0),$ $B(a\mid 0)$ und $C(a\mid f(a))$ mit $a\in\mathbb{R}$ und $0\lt a\lt 5$ festgelegt.

2.3.3

Zeichne eine mögliche Lage des Logos in die grafische Darstellung der Aufgabe 2.2.

(1 BE)

2.3.4

Berechne den Wert für $a$ so, dass der Flächeninhalt des Logos $ABC$ möglichst groß wird und ermittle den maximal möglichen Flächeninhalt des Logos.

(5 BE)

2.3.5

Um die Rutsche zu stabilisieren, wird eine geradlinig verlaufende Strebe vom Punkt $A$ zu einem Punkt auf dem Handlauf geplant. Dieser Punkt wird mit $D$ bezeichnet. Die Strebe soll in $D$ senkrecht auf den Handlauf treffen.

Beschreibe, wie die Koordinaten von $D$ rechnerisch ermittelt werden können.

Ein Computeralgebrasystem liefert die möglichen $x$ -Koordinaten $x_{D1}\approx -0,02,$ $x_{D2}\approx 1,04$ und $x_{D3}\approx 2,16.$ Berechne die Koordinaten von $D$ so, dass die Strebe möglichst kurz wird.

(7 BE)

2.4

An einer anderen Stelle auf dem Spielplatz soll ein weiteres Spielgerät errichtet werden, das vollständig aus einer Gummimischung hergestellt wird. Die Firma HL-Bau bietet solche Spielgeräte an, die 3,00 m lang sind und über die gesamte Länge einen gleichbleibenden Querschnitt haben.

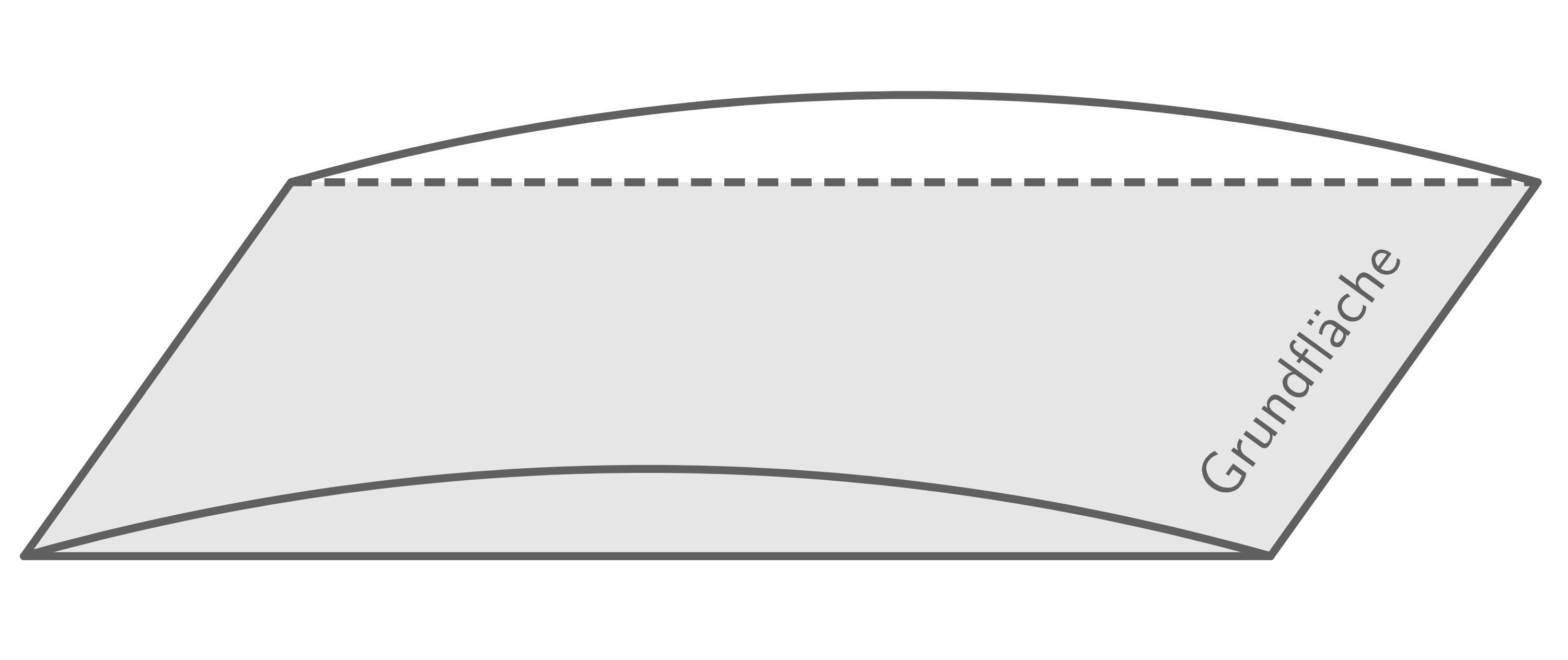
Mecklenburg-Vorpommern Abi 2022 Spielplatz

Abbildung: Beispiel eines solchen Spielgeräts

$\,$

In einem Koordinatensystem werden die Querschnitte dieser Spielgeräte vollständig begrenzt durch die $x$ -Achse und eine Parabel. Diese Parabeln sind Graphen der Funktionen $h_a$ mit $h_a(x)=a\cdot x^2+0,3$ und $a\lt 0,a\in\mathbb{R}.$ Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

2.4.1

Beschreibe, wie der Parameter $a$ Breite und Höhe der Spielgeräte beeinflusst.

(3 BE)

2.4.2

Für den Spielplatz wurde ein solches Spielgerät mit $a=-0,075$ hergestellt.

Weise nach, dass das Spielgerät eine Grundfläche von $12\,\text{m}^2$ hat.

Ermittle das zur Herstellung des Spielgerätes benötigte Volumen der Gummimischung.

(6 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$f_t(x)=(x^2-2x)\cdot (x-t)$ $=x\cdot (x-2)\cdot (x-t)$

Satz vom Nullprodukt anwenden: Ein Produkt ist genau dann Null, wenn einer der Faktoren Null ist. Deshalb folgen die Nullstellen $x_1=0,$ $x_2=2$ und $x_3=t.$

1.2

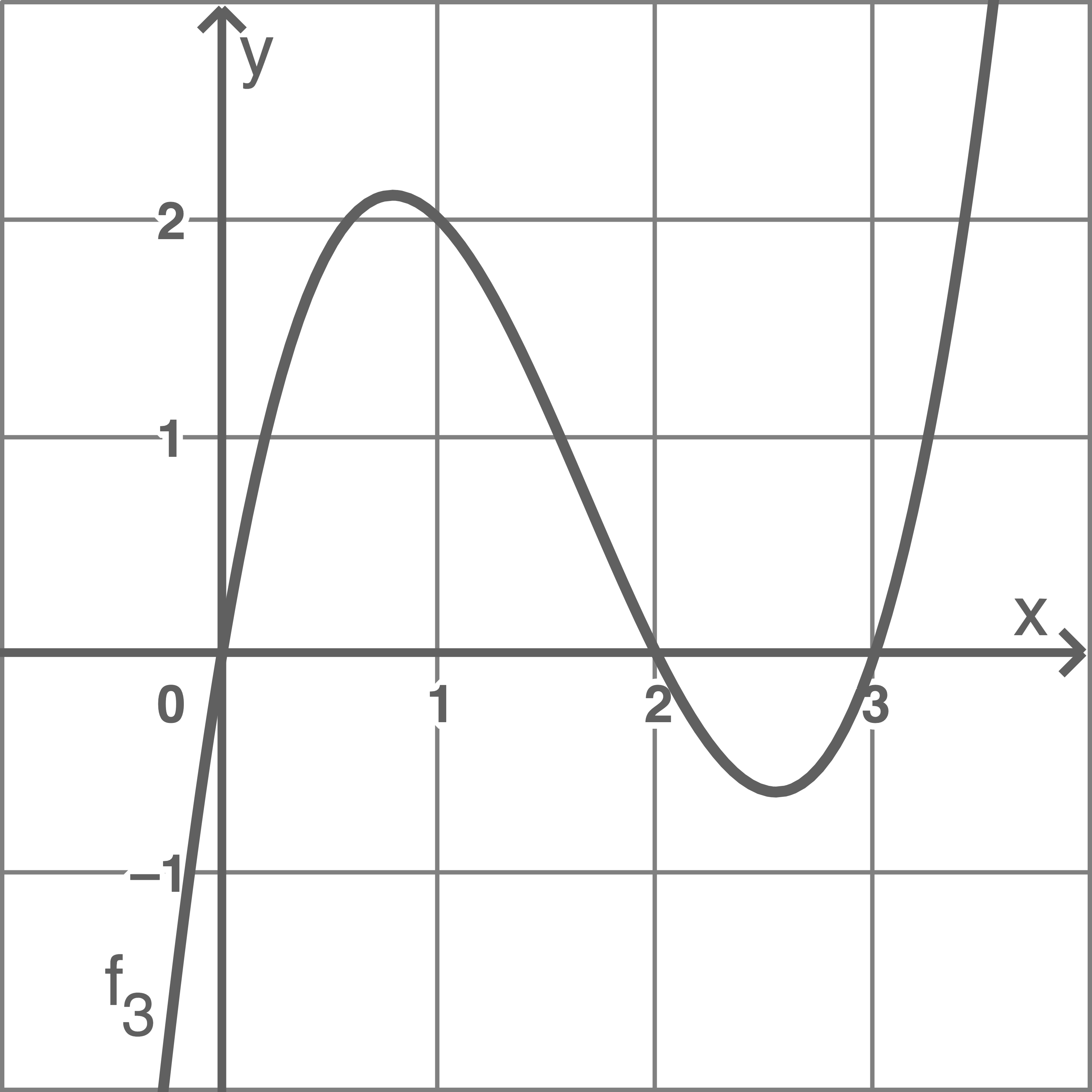
Mecklenburg-Vorpommern Abi 2022 Funktionenschar

1.3

Mit dem CAS wird die erste Ableitung bestimmt:

$\(f_t$ $=2x^2-2tx-2x+2t+x^2-2x$ $=3x^2-4x-2tx+2t$

Notwendige Bedingung für Extremstellen anwenden:

$\(f_t$

$3\cdot 0^2-4\cdot 0-2t\cdot 0+2t=22$

Es ergibt sich $2t=22,$ also $t=11.$

1.4

Aus 1.1 folgt, dass $f_5$ die Nullstellen $x_1=0,$ $x_2=2$ und $x_3=5$ hat. Zwischen der Nullstelle $x_2=2$ und $x_3=5$ verläuft der Graph von $f_5$ unterhalb der $x$ -Achse.

$A=\displaystyle\int_{0}^{2}f_5(x)\;\mathrm dx+\left|\displaystyle\int_{2}^{5}f(x)\;\mathrm dx\right|$ $=\dfrac{16}{3}+\dfrac{63}{4}=\dfrac{253}{12}\approx 21,1$

1.5

Die gesuchten Werte für $t$ sind $t=1$ und $t=4.$

Für $t=2$ schließt der Graph von $f_t$ nur eine Fläche mit den Koordinatenachsen ein, da $t$ mit der zweiten Nullstelle übereinstimmt.

Der Wert von $t$ bestimmt die Lage der beiden Teilflächen.

Fall 1: $t\gt 2$

$\displaystyle\int_{0}^{2}f_t(x)\;\mathrm dx=-\displaystyle\int_{2}^{t}f_t(x)\;\mathrm dx$

Nach $t$ aufgelöst ergibt sich mit dem CAS: $t_1=0$ und $t_2=4$

Da $t\gt 0,$ entfällt die Lösung $t_1=0.$

Fall 2: $0\lt t\lt 2$

$\displaystyle\int_{0}^{t}f_t(x)\;\mathrm dx=-\displaystyle\int_{t}^{2}f_t(x)\;\mathrm dx$

Nach $t$ aufgelöst ergibt sich mit dem CAS: $t_3=1$

2.1

Schnittpunkt mit der $y$ -Achse: $f(0)=0,3,$ also folgt $S_y(0\mid 0,3)$

Extrempunkte bestimmen

Mit der Produktregel folgt:

$\(\begin{array}[t]{rll} f$

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} f$

Es ist stets $\mathrm e^{-2 x} \neq 0.$

Mit dem Satz vom Nullprodukt folgt also

$\begin{array}[t]{rll} -40 x^2+38 x+1&=& 0 &\quad \scriptsize \mid\;:(-40) \\[5pt] x^2-0,95-0,025&=& 0 \end{array}$

Mit der $pq$ - Formel folgt $x_{1/2}= -\dfrac{-0,95}{2} \pm \sqrt{\left(\dfrac{-0,95}{2} \right)^2 -(-0,025)}$ $=\dfrac{19}{40} \pm \sqrt{\dfrac{401}{1600}}$

$x_1\approx -0,026$ und $x_2\approx 0,976$

Hinreichende Bedingung für Extremstellen anwenden

$\(f$

Es gilt:

$\(f$ also liegt ein lokales Minimum vor

$\(f$ also liegt ein lokales Maximum vor

$y$ -Koordinaten bestimmen

$f(-0,026)\approx 0,287$

$f(0,976)\approx 3,144$

$T(-0,026\mid 0,287),$ $H(0,976\mid 3,144)$

Wendepunkte bestimmen

Notwendige Bedingung für Wendestellen anwenden:

$\(\begin{array}[t]{rll} f$

Mit dem solve-Befhel des CAS folgen $x_1\approx 0,267$ und $x_2\approx 1,683.$

Auf die Anwendung der hinreichenden Bedingung für Wendestellen kann verzichtet werden, da in der Aufgabenstellung gegeben ist, dass $G$ zwei Wendepunkte besitzt. Die $y$ -Koordinaten folgen mit:

$f(0,267)\approx 1,29$

$f(1,682)\approx 2,316$

Die Koordinaten der Wendepunkte sind also $W_1(0,267\mid 1,29)$ und $W_2(1,682\mid 2,314).$

2.2

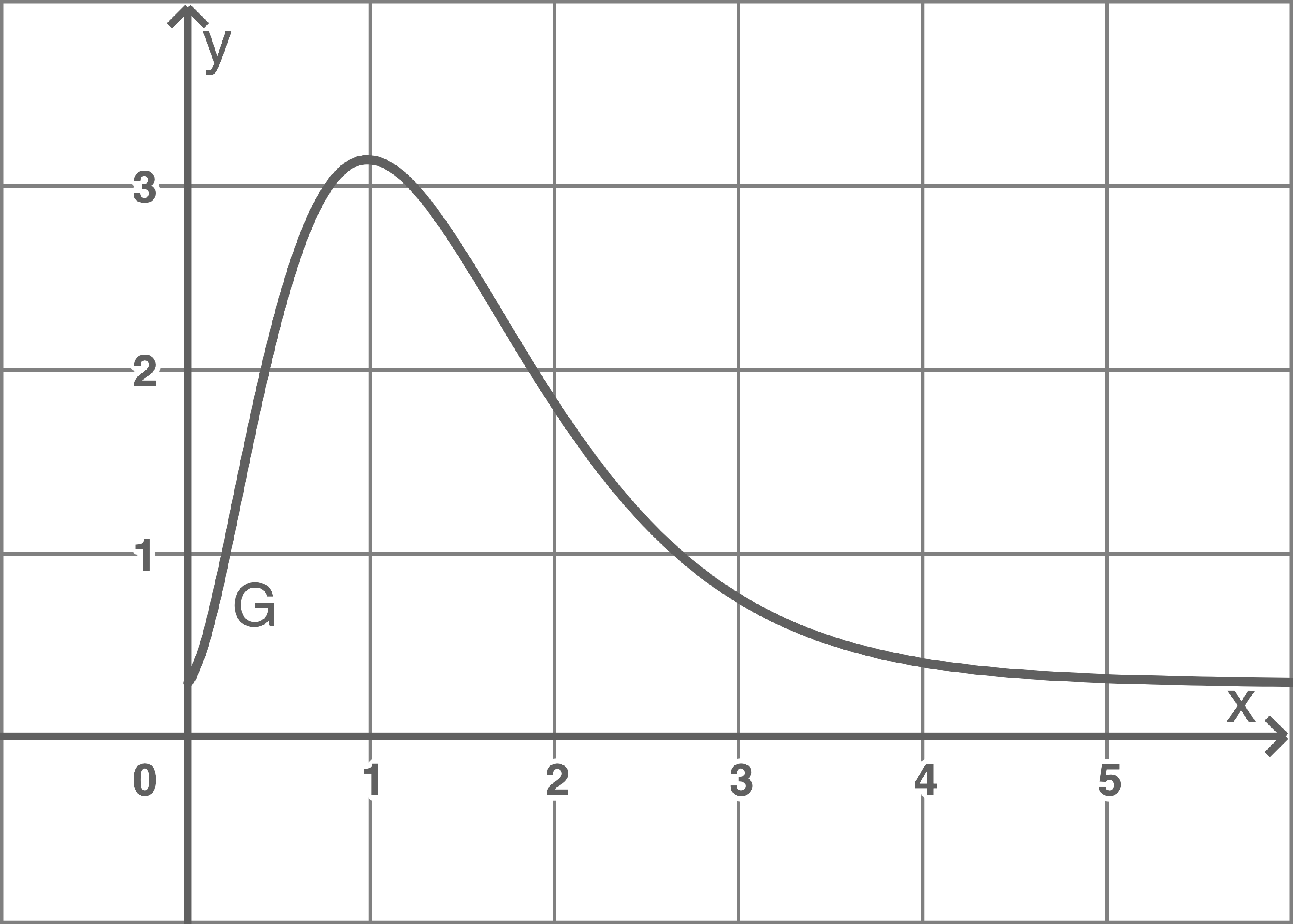
2.3.1

Es gilt: $f(5)\approx 0,32$

Die Höhe des Handlaufs über dem Erdboden am Ende der Rutsche beträgt $32\;\text{cm}.$

2.3.2

Fläche einseitig: $A=\displaystyle\int_{0}^{5}f(x)\;\mathrm dx$

Mit dem CAS ergeben sich die Kosten zu: $2\cdot A\cdot 202,20\,\dfrac{€}{\text{m}^2}\approx 2724,05\,€$

Die Kosten betragen ca. 2724 €.

2.3.3

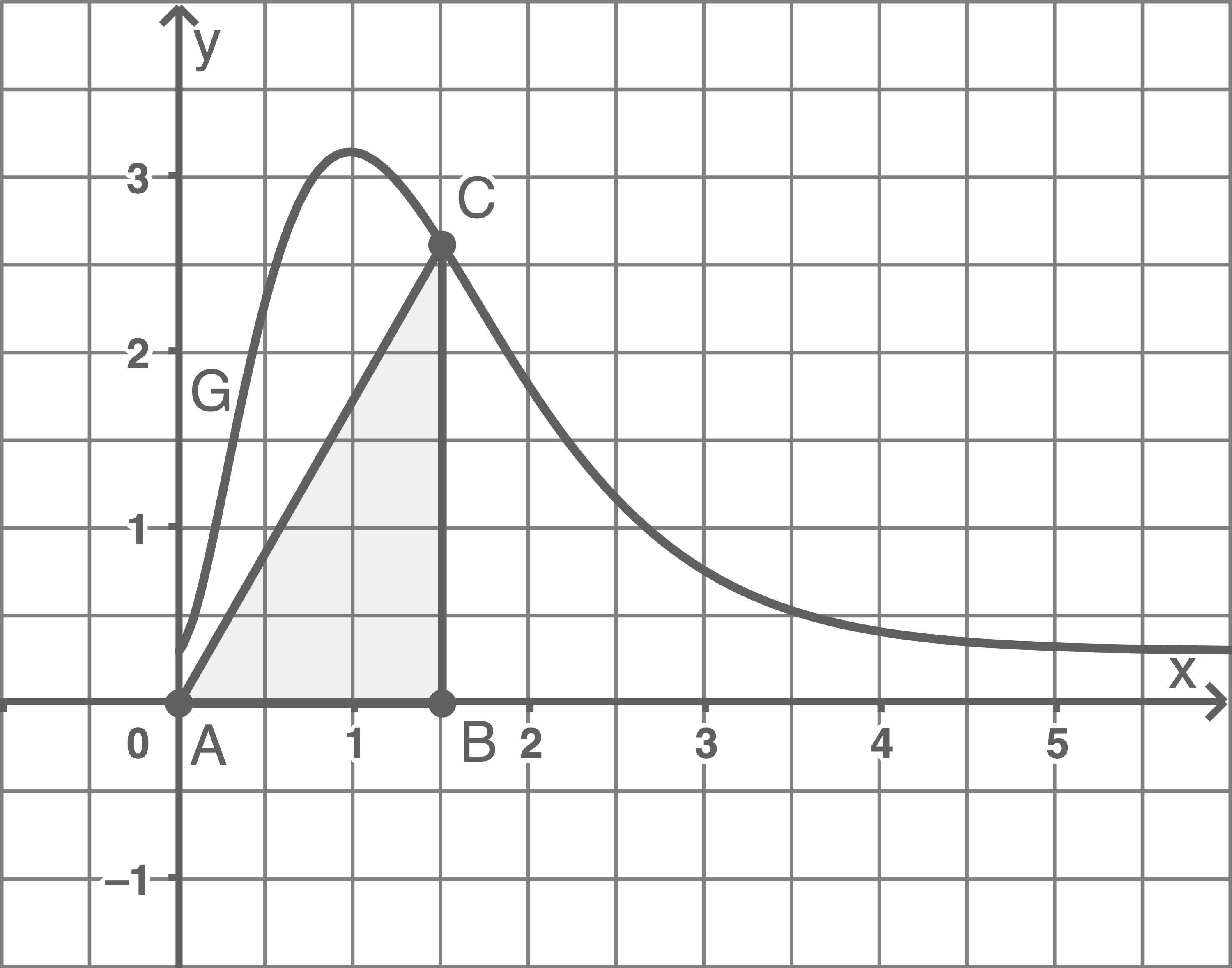
2.3.4

Mit $\overline{A B}=a$ und $\overline{B C}=f(a)$ erhält man für den Flächeninhalt des rechtwinkligen Dreiecks $ABC$ die Zielfunktion $A$ mit $A(a)=\dfrac{a \cdot f(a)}{2}.$

Dieser Flächeninhalt soll im vorgegebenen Intervall maximal werden, also muss $A$ mit dem CAS auf Extremstellen untersucht werden.

$A^{\prime}(a)=0,$ daraus folgt: $a_{1} \approx 1,55$ und $a_{2} \approx 4,51$

Aus $\(A$ folgt ein Maximum an $x= 1,55.$

Aus $\(A$ folgt ein Minimum an $x= 4,51.$

Es ist $A(1,55) \approx 1,96$

Die Zielfunktion hat ein Minimum bei $a \approx 4,51$ . Für $a\gt 4,51$ nimmt der Flächeninhalt daher wieder zu.

Die Randwertbetrachtung ergibt $A(5)\approx 0,81\lt 1,96.$

Strebt $a$ gegen 5, so strebt der Flächeninhalt gegen 0,81 und ist somit deutlich kleiner als an der Stelle $a_{1}.$

Für $a=1,55$ besitzt das Dreieck $ABC$ einen maximalen Flächeninhalt von ca. $2 \; \text{m}^2$ .

2.3.5

Die Strebe wird im Koordinatensystem als Ursprungsgerade durch $D\left(x_{D} \mid f\left(x_{D}\right)\right)$ mit dem Anstieg $m=\dfrac{f\left(x_{D}\right)}{x_{D}}$ dargestellt. Im Punkt $D$ schneidet diese Ursprungsgerade den Graphen von $f$ senkrecht. Der Anstieg des Graphen von $f$ an der Stelle $x_{D}$ (bzw. der Tangente an dieser Stelle) entspricht $\(f$

Da beide Graphen senkrecht zueinanderstehen, gilt: $f^{\prime}\left(x_{D}\right) \cdot \dfrac{f\left(x_{D}\right)}{x_{D}}=-1$

Als Lösungen dieser Gleichung erhält man mit dem solve-Befehl des CAS die möglichen Stellen $x_{D}$ . Durch Berechnung der zugehörenden Funktionswerte ergeben sich die möglichen Koordinaten für $D$ .

Lösungen für $x_D \lt 0$ entfallen. Für alle anderen Lösungen $x_D$ lassen sich die Strebenlängen mit dem Satz des Pythagoras berechnen:

$|\overline{AD}|=\sqrt{x_D^{2}+(\mathrm{f}(x))^{2}}$

Für $x_{D2}$ folgt $|\overline{\mathrm{AD}}|=\sqrt{\left(\mathrm{x}_{\mathrm{D} 2}\right)^{2}+\left(\mathrm{f}\left(\mathrm{x}_{\mathrm{D} 2}\right)\right)^{2}}$ $=\sqrt{1,04^{2}+(\mathrm{f}(1,04))^{2}} \approx 3,3$ , für $\mathrm{x}_{\mathrm{D} 3}$ gilt $|\overline{\mathrm{AD}}|=\sqrt{\left(\mathrm{x}_{\mathrm{D} 3}\right)^{2}+\left(\mathrm{f}\left(\mathrm{x}_{\mathrm{D} 3}\right)\right)^{2}}$ $=\sqrt{2,16^{2}+(f(2,16))^{2}} \approx 2,67$ .

Somit ergibt sich für $D_{3}(2,16 \mid 1,57)$ die kürzeste Strebe.

2.4.1

Der Parameter $a$ beeinflusst die Breite des Spielgerätes. Je kleiner der Wert von $a$ (d. h. für $a \rightarrow-\infty$ ), desto schmaler wird das Spielgerät. Je größer der Wert von $a$ (d. h. für $a \rightarrow 0$ ), desto größer wird die Breite des Spielgeräts.

Auf die Höhe von $0,3\;\text{m}$ hat der Parameter keinen Einfluss.

2.4.2

$h_{-0,075}(x)=-0,075 x^{2}+0,3$

Die Breite des Spielgeräts ergibt sich aus dem Abstand der beiden Nullstellen von $h_{-0,075}:$

$h_{-0,075}(x)=0,$ daraus folgt mit dem solve-Befehl des CAS: $x_1=-2$ und $x_2=2$

$|-2|+2=4$

Die Breite beträgt $4 \; \text{m}.$

Die Grundfläche ist ein Rechteck mit den Seitenlängen $3 \;\text{m}$ und $4 \;\text{m}$ und besitzt demnach einen Flächeninhalt von $12 \;\text{m}^2$ .

Das Volumen ergibt sich aus dem Flächeninhalt $A_{Q}$ der Querschnittsfläche und der Länge $L$ des Spielgeräts:

$V=L \cdot A_{Q}=3 \cdot \displaystyle\int_{-2}^{2} h_{-0,075}(x)\; \mathrm{d}x$ $=3 \cdot 0,8=2,4 \;\text{m}^3$

Das benötigte Volumen der Gummimischung beträgt $2,4 \;\text{m}^3$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?