Wahlteil A1

A1 Analysis

Gegeben sind die Funktionen $f$ und $g$ mit ihren Gleichungen

$f(x) = -x^4+2x^2+1$ $\quad$ und $\quad$ $g(x)= -\dfrac{9}{1.280}x^4+\dfrac{9}{40}x^2-\dfrac{9}{5}$ $\quad$ sowie $x\in \mathbb{R}$ .

1.1

Berechne für den Graphen von $f$ die Koordinaten der Schnittpunkte mit den Koordinatenachsen sowie der Extrempunkte und bestimme die Art der Extrema.
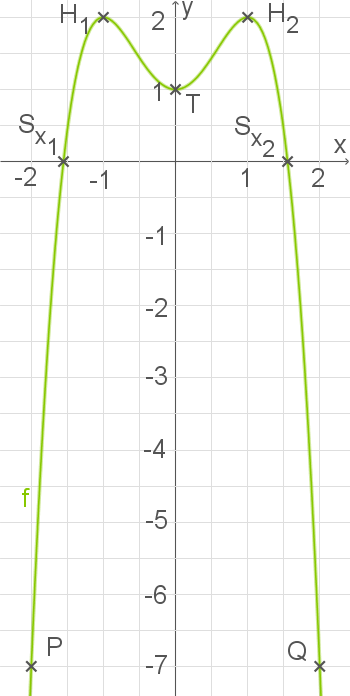
Zeichne diesen Graphen im Intervall $-2\leq x\leq 2$ in ein geeignetes Koordinatensystem.

1.2

Die Gerade mit der Gleichung $y=1,5$ schließt mit dem Graphen von $f$ mehrere Flächen vollständig ein. Bestimme den Gesamtinhalt dieser Flächen.

1.3

Weise nach, dass sich die Graphen von $f$ und $g$ nie unter einem rechten Winkel schneiden.

1.4

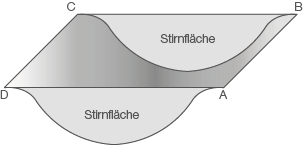
In der Praxis werden Flüssigkeiten in oben offenen Auffangbecken gespeichert, deren Boden gewölbt ist und deren ebene Stirnflächen senkrecht nach unten verlaufen.
Die mit $A$ , $B$ , $C$ und $D$ bezeichneten Eckpunkte des Beckens bilden ein Rechteck mit $\overline{AB} = 5\,\text{m}$ . Ein solches Becken hat überall denselben Querschnitt.

Diagramm mit zwei Stirnflächen und einer skizzierten Form.

Abb. 1

Im Modell wird dieser Querschnitt unten durch eine Parabel und oben durch eine Gerade begrenzt (siehe Abbildung 1). Im Koordinatensystem liegen die Gerade auf der $x$ -Achse und die Parabel symmetrisch zur $y$ -Achse. Die Parabel wird durch den Graphen der Funktion $g$ im Intervall $-4\leq x\leq 4$ erfasst. Eine Längeneinheit entspricht dabei einem Meter.

1.4.1

Aus Sicherheitsgründen dürfen die Wände ungesicherter Auffangbecken nirgends steiler als $30^{\circ}$ sein. Andernfalls müssen sie umzäunt werden. Überprüfe, ob die Errichtung eines Zauns für dieses Auffangbecken auch entlang der Seiten $AB$ und $CD$ erforderlich ist.

1.4.2

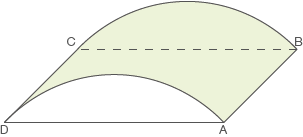
Gegen Witterungseinflüsse wird dieses Becken mit einer an den Stirnseiten offenen Kunststoffhaube geschützt (siehe Abbildung 2). Ihr Querschnitt wird durch den Graphen der Funktion $q(x)= -\frac{1}{8}x^2+2$ im Intervall $-4\leq x \leq 4$ modelliert ( $x \in \mathbb{R}$ ).
Bestimme die Größe der Fläche der Abdeckung.

Diagramm eines geometrischen Figures mit den Punkten A, B, C und D.

Abb. 2

1.4.3

Das Auffangbecken ist bis zu einem Drittel seiner Höhe gefüllt. Ermittle, wie viel Liter Flüssigkeit noch in das Becken fließen können, sodass es randvoll gefüllt ist.

Bildnachweise [nach oben]

[1]

[2]

A1 Analysis

1.1

$\blacktriangleright$ Koordinaten der Schnittpunkte mit den Achsen berechnen

Gesucht sind die Schnittpunkte des Graphen von $f$ mit den Koordinatenachsen. Die $y$ -Koordinate eines Schnittpunkts mit der $x$ -Achse ist immer $0$ . Setze also $f(x)=0$ , und löse die Gleichung nach der passenden $x$ -Koordinate auf.

Der Schnittpunkt mit der $y$ -Achse befindet sich immer an der Stelle $x=0$ . Setze also $x = 0$ in den Funktionsterm ein, um die passende $y$ -Koordinate zu berechnen.

Beide Rechnungen kannst du mit deinem CAS durchführen. Definiere dazu zuerst die Funktion $f$ . Die Gleichung $f(x)=0$ kannst du mit dem solve-Befehl lösen.

Du erhältst dann folgende Ergebnisse:

$x = \pm \sqrt{\sqrt{2}+1}$ und $f(0)= 1$

Der Graph von $f$ schneidet die $x$ -Achse also in den Punkten $S_{x_1}\left(-\sqrt{\sqrt{2}+1}\mid 0 \right)$ und $S_{x_2}\left(\sqrt{\sqrt{2}+1}\mid 0 \right)$ und die $y$ -Achse im Punkt $S_y(0\mid 1)$ .

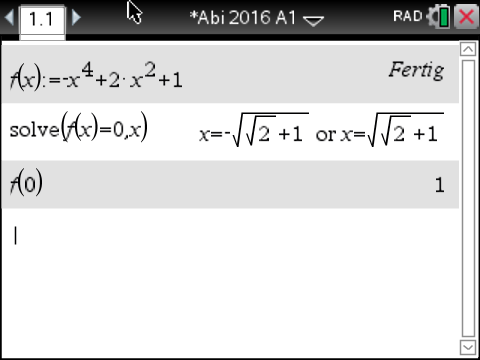Mathematische Eingabe mit einer Funktion und deren Lösung in einer Softwareanwendung.

Abb. 1: Schnittpunkte mit den Achsen

$\blacktriangleright$ Koordinaten und Art der Extrema bestimmen

Du hast die Funktion $f$ gegeben und sollst deren Graph auf Extrempunkte untersuchen. Für eine Extremstelle $x_E$ benötigst du die beiden folgenden Kriterien:

Notwendiges Kriterium: $\, f‘(x_E)=0$
Hinreichendes Kriterium:
- Ist $f‘‘(x_E)\gt 0$ , handelt es sich um eine Minimalstelle.
- Ist $f‘‘(x_E)\lt 0$ , handelt es sich um eine Maximalstelle.

Du kannst also wie folgt vorgehen:

Bestimme die ersten beiden Ableitungsfunktionen $f‘$ und $f‘‘$ .
Wende das notwendige Kriterium an, indem du $f‘(x)=0$ setzt und nach $x$ löst.
Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in $f‘‘(x)$ einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
Berechne die Funktionswerte von $f$ an den Extremstellen.

1. Schritt: Ableitungsfunktionen bestimmen

Die Ableitungen kannst du ebenfalls in deinem CAS definieren. Nutze dazu den Ableitungsbefehl, den du wie folgt findest:

menu $\to$ 4: Analysis $\to$ 1: Ableitung

Mathematische Gleichungen in einer Software zur Lösung von Differentialgleichungen.

Abb. 2: Ableitungen

2. Schritt: Notwendiges Kriterium anwenden

Durch Gleichsetzen von $f‘(x)$ mit Null, erhältst du mögliche Extremstellen. Die Gleichung kannst du ebenfalls mit dem solve-Befehl deines CAS lösen und erhältst dann folgendes Ergebnis:

$x_1 = -1$ , $x_2 = 0$ und $x_3 = 1$

Screenshot einer mathematischen Software mit Ableitungen und Gleichungen.

Abb. 3: Notwendiges Kriterium

3. Schritt: Hinreichendes Kriterium überprüfen

Du hast drei mögliche Extremstellen bestimmt. Setze diese in die zweite Ableitungsfunktion $f‘‘(x)$ ein, um sie zu überprüfen. Du erhältst folgende Ergebnisse:

$f‘‘(-1)= -8$ , Maximalstelle
$f‘‘(0)=4$ , Minimalstelle
$f‘‘(1)= -8$ Maximalstelle

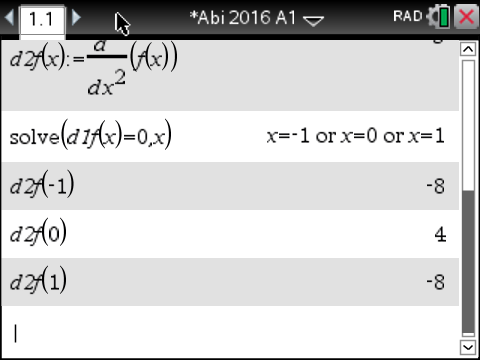Mathematische Berechnungen und Lösungen in einer Softwareoberfläche, inklusive Ableitungen und Funktionswerte.

Abb. 4: Hinreichendes Kriterium

4. Schritt: Funktionswerte berechnen

Berechne nun die vollständigen Koordinaten der drei Extrempunkte, indem du die Extremstellen jeweils in $f(x)$ einsetzt. Dies kannst du wie zuvor mit deinem CAS tun. Du erhältst dann folgende Koordinaten:

$H_1 (-1 \mid 2)$ $\quad$ $T(0\mid 1)$ $\quad$ $H_2(1\mid 2)$

Der Graph von $f$ besitzt zwei Hochpunkte $H_1 (-1 \mid 2)$ und $H_2(1\mid 2)$ sowie einen Tiefpunkt $T(0\mid 1)$ .

$\blacktriangleright$ Graph zeichnen

Du sollst den Graphen der Funktion $f$ im Intervall $-2 \leq x \leq 2$ zeichnen. Du kennst bereits die Koordinaten der Schnittpunkte mit den Koordinatenachsen sowie der Extrempunkte.
Berechne zusätzlich die Funktionswerte an den Randstellen $x_1 = -2$ und $x_2 =2$ . Zeichne anschließend ein geeignetes Koordinatensystem und trage die Punkte ein. Nutze diese Punkte zur Orientierung.

$f(-2) = -7$ , $\quad f(2)=-7$

Graph einer Funktion mit grüner Kurve und Achsenbeschriftungen.

Abb. 5

1.2

$\blacktriangleright$ Flächeninhalt berechnen

Du sollst den Gesamtinhalt der Flächen berechnen, die die Gerade $h$ mit $y=1,5$ mit dem Graphen von $f$ einschließt. Ergänze dazu in deiner Abbildung des Graphen von $f$ die Gerade.

Du siehst, dass insgesamt $3$ Flächen vollständig eingeschlossen werden.
$f$ ist eine gerade Funktion, also ist der Graph von $f$ symmetrisch zur $y$ -Achse. Die beiden grünen Flächen besitzen daher den gleichen Flächeninhalt $A_1 = A_3$ .

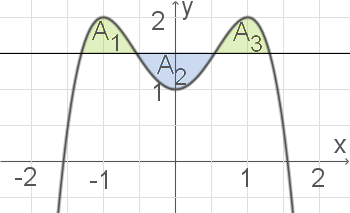Graph einer Funktion mit farblich markierten Bereichen A1, A2 und A3 auf einem Koordinatensystem.

Abb. 6: Eingeschlossene Flächen

Die einzelnen Flächeninhalte $A_1$ und $A_2$ kannst du jeweils mit Hilfe eines Integrals über die Differenzfunktion $f-h$ berechnen. Wähle als Grenzen die entsprechenden Schnittstellen der beiden Funktionen. Beachte, dass Flächeninhalte immer positiv sind.

1. Schritt: Schnittstellen berechnen

Die Schnittstellen von $f$ und der Gerade $h$ kannst du durch Gleichsetzen der Funktionsterme mit deinem CAS berechnen:

$\begin{array}[t]{rll} f(x)&=&h(x) \\[5pt] f(x)&=& 1,5 \end{array}$

Löse mit dem solve-Befehl. Du erhältst dann folgende Ergebnisse:

$x_1 \approx -1,31$
$x_2 \approx -0,54$
$x_3 \approx 0,54$
$x_4 \approx 1,31$

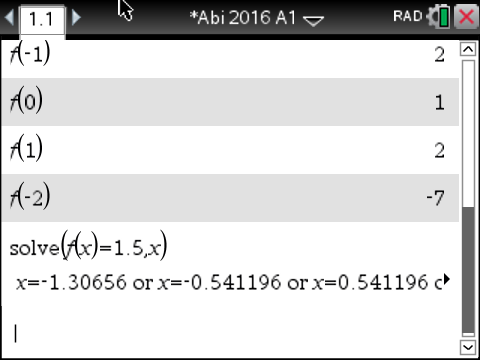Screenshot einer mathematischen Berechnung mit Funktionen und Lösungen.

Abb. 7: Schnittstellen der Funktionen

2. Schritt: Integrale berechnen

Gesucht sind also folgende Integrale:

$A_1 = \left| \displaystyle\int_{-1,3}^{-0,54}(f(x)-h(x))\;\mathrm dx\right|$ und $A_2 = \left| \displaystyle\int_{-0,54}^{0,54}(f(x)-h(x))\;\mathrm dx\right|$

Du kannst die Integrale ebenfalls mit deinem CAS berechnen. Den Befehl findest du unter:

menu $\to$ 4: Analysis $\to$ 3: Integral

Du erhältst folgende Ergebnisse:

$A_1 \approx 0,25$
$A_2 \approx 0,35$

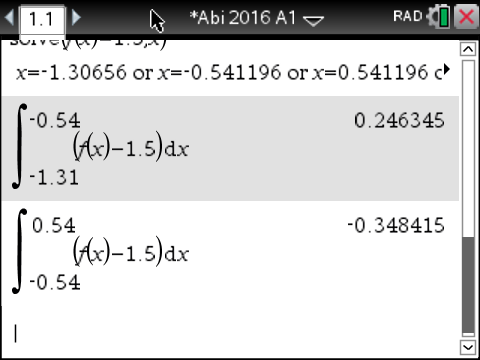Mathematische Berechnungen mit Integralen und Resultaten auf einem Bildschirm.

Abb. 8: Berechnung der Integrale

Der Gesamtflächeninhalt ergibt sich dann wie folgt:

$\begin{array}[t]{rll} A&=& 2\cdot A_1 + A_2\\[5pt] &\approx& 2\cdot 0,25 + 0,35 \\[5pt] &=& 0,85 \end{array}$

Der Graph von $f$ und die Gerade mit $y =1,5$ schließen Flächen mit einem Gesamtflächeninhalt von ca. $0,85\,\text{[FE]}$ ein.

1.3

$\blacktriangleright$ Schnittwinkel überprüfen

Du sollst nachweisen, dass sich die Graphen von $f$ und $g$ nie im rechten Winkel schneiden. Berechne dazu die Schnittstellen von $f$ und $g$ und überprüfe, ob sich die Graphen dort im rechten Winkel schneiden. Zwei Graphen schneiden sich im rechten Winkel, wenn für die Steigungen der beiden Graphen im Schnittpunkt folgendes gilt:

$m_f\cdot m_g = -1$

Berechne also anschließend die Steigungen der beiden Graphen in den Schnittpunkten und überprüfe die Gleichung. Die Steigung eines Graphen wird durch die erste Ableitungsfunktion beschrieben.

1. Schritt: Schnittstellen berechnen

Die Schnittstellen kannst du wie zuvor mit deinem CAS berechnen, indem du $f(x)$ und $g(x)$ gleichsetzt. Du erhältst dann folgendes Ergebnis:

$x_{1,2} =\pm 4\cdot\sqrt{\dfrac{ \sqrt{22.835} + 71}{1.271}}$

2. Schritt: Gleichung überprüfen

Mit deinem CAS kannst du direkt $f‘(x)\cdot g‘(x)$ berechnen.

$f‘(x_1)\cdot g‘(x_1) \approx -7,46 \neq -1$

$f‘(x_2)\cdot g‘(x_2) \approx -7,46 \neq -1$

Die Gleichung ist in den Schnittpunkten also nicht erfüllt. Die Graphen von $f$ und $g$ schneiden sich in keinem Punkt im rechten Winkel.

1.4.1

$\blacktriangleright$ Errichtung eines Zauns überprüfen

Ein Zaun muss errichtet werden, wenn der Boden um mehr als $30^{\circ}$ abfällt. Der Verlauf des Bodens wird durch eine Parabel mit der Funktion $g$ beschrieben, die symmetrisch zur $y$ -Achse ist. Es genügt also, wenn du den rechten Teil des Bodens betrachtest.

In diesem Teil steigt der Graph von $g$ . Berechne also die Stelle mit der größten Steigung der Parabel und anschließend den Steigungswinkel an dieser Stelle. Ist dieser kleiner als $30^{\circ}$ , müssen keine Zäune errichtet werden.

Da die Steigung eines Graphen durch die erste Ableitung beschrieben wird, ist also die globale Maximalstelle der ersten Ableitung $g‘$ im Intervall $[-4;4]$ gesucht. Berechne dazu wie in Aufgabenteil a) mit Hilfe des notwendigen und hinreichenden Kriteriums die lokalen Maxima von $g‘$ und überprüfe anschließend noch auf Randextrema. Achte darauf, dass du nun nicht Extremstellen von $g$ , sondern von $g‘$ berechnen sollst.

1. Schritt: Notwendiges Kriterium anwenden

Da lokale Extremstellen von $g‘$ gesucht sind, musst du $g‘‘(x)=0$ setzen. Dies kannst du wieder mit deinem CAS tun und erhältst folgende Lösungen:

$\begin{array}[t]{rll} g‘‘(x)&=&0 \\[5pt] x_1&=& \dfrac{-4\cdot \sqrt{3}}{3} \\[5pt] x_2&=& \dfrac{4\cdot \sqrt{3}}{3} \end{array}$

Mathematische Gleichungen und Ableitungen auf einem Bildschirm dargestellt.

Abb. 9: Notwendiges Kriterium

2. Schritt: Hinreichendes Kriterium überprüfen

Setze nun $x_1$ und $x_2$ in die dritte Ableitung ein, um die Maximalstelle zu identifizieren. Du erhältst folgendes Ergebnis:

$\begin{array}[t]{rll} g‘‘‘(x_1)&=&g‘‘‘\left(\dfrac{-4\cdot \sqrt{3}}{3}\right) \\[5pt] &=& \dfrac{9\cdot \sqrt{3} }{40}\gt 0\\[10pt] g‘‘‘(x_2)&=& g‘‘‘\left(\dfrac{4\cdot \sqrt{3}}{3}\right) \\[5pt] &=& \dfrac{-9\cdot \sqrt{3} }{40}\lt 0 \\[5pt] \end{array}$

An der Stelle $x_2 = \dfrac{4\cdot \sqrt{3} }{3}\approx 2,31$ befindet sich also ein lokales Maximum von $g‘$ .

3. Schritt: Randextrema überprüfen

Berechne nun den Funtionswert $g‘(x)$ , an der lokalen Maximalstelle und den Intervallgrenzen, um die globale Maximalstelle zu bestimmen.

$\begin{array}[t]{rll} g‘(-4)&=& 0 \\[5pt] g‘(4)&=& 0 \\[5pt] g‘\left(\dfrac{4\cdot \sqrt{3}}{3}\right)&=& \dfrac{2\cdot\sqrt{3}}{5} \\[5pt] \end{array}$

Die größte Steigung im betrachteten Intervall hat der Graph von $g$ also an der Stelle $\dfrac{4\cdot \sqrt{3}}{3}$ .

4. Schritt: Steigungswinkel berechnen

Anhand der Steigung $m$ des Graphen von $g$ kannst du nun den Steigungswinkel $\alpha$ an der steilsten Stelle berechnen:

$\tan(\alpha) = m$

$\begin{array}[t]{rll} \tan(\alpha)&=& m \\[5pt] \tan(\alpha)&=& \dfrac{2\cdot\sqrt{3}}{5} \\[5pt] \alpha &\approx& 34,7^{\circ} \end{array}$

Vollständige Lösung anzeigen

An der steilsten Stelle fällt die Wand in einem Winkel von ca. $34,7^{\circ}$ . Es muss also ein Zaun errichtet werden.

1.4.2

$\blacktriangleright$ Größe der Abdeckungsfläche berechnen

Du sollst die Größe der Fläche der Abdeckung berechnen. Diese Fläche kannst du als Rechteck betrachten. Zwei gegenüberliegende Seiten des Rechtecks sind die Seiten $\overline{AB}$ und $\overline{CD}$ , deren Längen du in der Aufgabenstellung gegeben hast. Der Verlauf der anderen beiden Seiten wird durch den Graphen der Funktion $q$ zwischen den beiden Punkten $A$ und $D$ beschrieben. Die Länge dieser beiden Seiten des Rechtecks ergibt sich also aus der Bogenlänge des Graphen von $q$ im Intervall $[-4,4]$ . Diese kannst du mit folgender Formel berechnen:

$s_{f[a;b]}$ $= \displaystyle\int_{a}^{b}\sqrt{1+\left(f‘(x)\right)^2}\;\mathrm dx$

Die Länge der Seite $\overline{AB}$ beträgt $5\,\text{m}$ . Berechne nun die verbleibende Seitenlänge mit Hilfe der Formel.

Setze also in die Formel ein. Das Integral kannst du mit Hilfe des CAS berechnen. Den Befehl dafür findest du unter

menu $\to$ 4: Analysis $\to$ 3: Integral

$s_{q[-4;4]} \approx 9,18 \,\text{[m]}$

Vollständige Lösung anzeigen

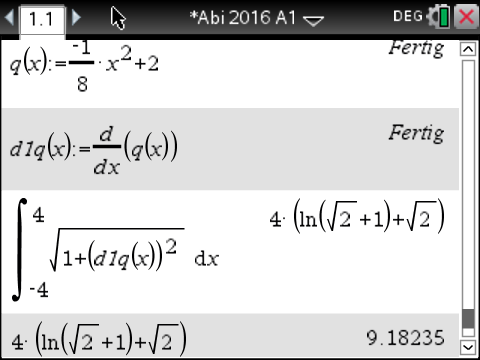Mathematische Gleichungen und Integrale auf einem Bildschirm dargestellt.

Abb. 10: Integralberechechnung

Die Größe der Fläche der Abdeckung ergibt sich also wie folgt:

$\begin{array}[t]{rll} A&\approx& 5\,\text{m} \cdot 9,18 \,\text{m} \\[5pt] &=& 45,9\,\text{m}^2 \end{array}$

Die Fläche der Abdeckung ist ca. $45,9\,\text{m}^2$ groß.

1.4.3

$\blacktriangleright$ Volumen des Wassers berechnen

Das Becken ist bis zu einem Drittel seiner Höhe gefüllt. Gesucht ist das Volumen an Wasser, das noch in das Becken passt. Dazu musst du die Größe der Querschnittsfläche des noch leeren Beckenteils mit der Länge des Beckens multiplizieren. Zuerst musst du also die Größe der Querschnittsfläche des leeren Beckenteils berechnen.

Betrachte die Skizze. Die blaue Gerade $h$ modelliert den aktuellen Wasserstand. Einer der Schnittpunkte dieser Gerade mit dem Graphen von $g$ ist $S$ .

Du kannst erkennen, dass sich die Querschnittsfläche aus den beiden roten Flächen und der grünen Fläche zusammensetzt.

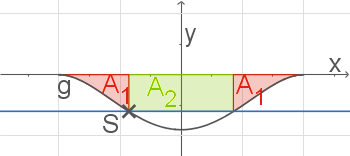Grafik eines Koordinatensystems mit einer Funktion, die rote und grüne Flächen zeigt.

Abb. 11: Querschnittsfläche

Da der Graph von $g$ symmetrisch zur $y$ -Achse ist und die roten Flächen Flächen zwischen dem Graphen von $g$ und der $x$ -Achse sind, besitzen die beiden roten Flächen die gleiche Größe $A_1$ . Diese kannst du mit einem Integral mit den Grenzen $-4$ und $x_S$ über $g$ berechnen, wobei $x_S$ die $x$ -Koordinate von $S$ , also die negative Schnittstelle von $g$ und $h$ ist.
Die grüne Fläche ist ein Rechteck, dessen Seitenlängen sich aus dem Betrag der Koordinaten von $S$ ergeben.

Du musst also die Koordinaten von $S$ berechnen, indem du $g(x) =h(x)$ setzt. Dafür benötigst du die Geradengleichung von $h$ . Da $h$ ein Drittel der Beckenhöhe modelliert, musst du zunächst die Tiefe des gesamten Beckens berechnen. Da der Graph von $g$ symmetrisch zur $y$ -Achse ist, liegt der tiefste Punkt genau an der Stelle $y=0$ . Die Tiefe des Beckens ergibt sich also aus dem Funktionswert von $g$ an der Stelle $y=0$ .

1. Schritt: Geradengleichung aufstellen

Berechne die Tiefe des Beckens über $g(0)$ :

$g(0) = -\dfrac{9}{5}$

Vollständige Lösung anzeigen

Das Becken ist and er tiefsten Stelle also $\dfrac{9}{5} \,\text{m}$ tief. Das Becken ist zu einem Drittel gefüllt, also verläuft die Gerade in einer Höhe von $-\dfrac{9}{5} + \dfrac{9}{5}\cdot \dfrac{1}{3} = -\dfrac{6}{5}$ :

$h(x)= -\dfrac{6}{5}$

2. Schritt: Koordinaten des Schnittpunkts berechnen

Setze $g(x)=h(x)$ . Die Gleichung kannst du mit dem solve-Befehl deines CAS lösen. Du erhältst folgendes Ergebnis:

$\begin{array}[t]{rll} x_1&=& ... \approx -5,39\\[5pt] x_2&=& ... \approx-1,71 \\[5pt] x_3&=& ... \approx 1,71\\[5pt] x_4&=& ...\approx 5,39 \\[5pt] \end{array}$

Vollständige Lösung anzeigen

$x_1$ und $x_4$ fallen aus der Betrachtung raus, da die Modellierung nur den Bereich $-4 \leq x \leq 4$ betrifft. Der Punkt $S$ aus der Skizze besitzt also folgende Koordinaten

$S\left(\frac{-4\cdot \sqrt{-3\cdot \left(\sqrt{6} -3\right)}}{3}\,\bigg \vert \, -\frac{6}{5}\right)$

3. Schritt: Größe der Querschnittsfläche berechnen

Die Größe der gesamten Querschnittsfläche $A$ setzt sich wie folgt zusammen:

$A = 2\cdot A_1 + A_2$

$A_2$ kannst du über die Beträge der Koordinaten von $S$ berechnen:

$A_2 \approx 4,11$

Vollständige Lösung anzeigen

$A_1$ kannst du mit Hilfe eines Integrals über der Funktion $g$ berechnen. Als Grenzen wählst du $a= -4$ und $b= x_S = \dfrac{-4\cdot \sqrt{-3\cdot \left(\sqrt{6} -3\right)}}{3}$ . Das Integral kannst du wie zuvor mit deinem CAS berechnen und erhältst dann folgendes Ergebnis:

$A_1 \approx 1,11$

Vollständige Lösung anzeigen

Insgesamt ergibt sich dann die Größe der Querschnittsfläche wie folgt:

$\begin{array}[t]{rll} A&=&2\cdot A_1 +A_2 \\[5pt] &\approx& 2\cdot 1,11 + 4,11 \\[5pt] &=&6,33 \,\left[\text{m}^2\right] \end{array}$

4. Schritt: Volumen berechnen

Das Becken ist $5\,\text{m}$ lang. Also ergibt sich folgendes Volumen:

$\begin{array}[t]{rll} V&\approx& 6,33 \,\text{m}^2 \cdot 5\,\text{m} \\[5pt] &=& 31,65 \,\text{m}^3 \\[5pt] &=& 31.650 \,\text{dm}^3 \\[5pt] &=& 31.650\,l \\[5pt] \end{array}$

Bis das Becken randvoll gefüllt ist, passen noch ca. $31.650\,l$ in das Becken.

Bildnachweise [nach oben]

[1]-[11]

A1 Analysis

1.1

$\blacktriangleright$ Koordinaten der Schnittpunkte mit den Achsen berechnen

Der Schnittpunkt mit der $y$ -Achse befindet sich immer an der Stelle $x=0$ . Setze also $x = 0$ in den Funktionsterm ein, um die passende $y$ -Koordinate zu berechnen.

Beide Rechnungen kannst du mit deinem CAS durchführen. Definiere dazu zuerst die Funktion $f$ . Die Gleichung $f(x)=0$ kannst du mit dem solve-Befehl lösen.

Du erhältst dann folgende Ergebnisse:

$x = \pm \sqrt{\sqrt{2}+1}$ und $f(0)= 1$

Mathematische Software mit Gleichungsdefinition und Lösung für f(x) = 0.

Abb. 1: Schnittpunkte mit den Achsen

$\blacktriangleright$ Koordinaten und Art der Extrema bestimmen

Du hast die Funktion $f$ gegeben und sollst deren Graph auf Extrempunkte untersuchen. Für eine Extremstelle $x_E$ benötigst du die beiden folgenden Kriterien:

Notwendiges Kriterium: $\, f‘(x_E)=0$
Hinreichendes Kriterium:
- Ist $f‘‘(x_E)\gt 0$ , handelt es sich um eine Minimalstelle.
- Ist $f‘‘(x_E)\lt 0$ , handelt es sich um eine Maximalstelle.

Du kannst also wie folgt vorgehen:

Bestimme die ersten beiden Ableitungsfunktionen $f‘$ und $f‘‘$ .
Wende das notwendige Kriterium an, indem du $f‘(x)=0$ setzt und nach $x$ löst.
Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in $f‘‘(x)$ einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
Berechne die Funktionswerte von $f$ an den Extremstellen.

1. Schritt: Ableitungsfunktionen bestimmen

Die Ableitungen kannst du ebenfalls in deinem CAS definieren. Nutze dazu den Ableitungsbefehl, den du wie folgt findest:

keyboard $\to$ Math2

Mathematische Definitionen von Ableitungen in einer Software-Anwendung.

Abb. 2: Ableitungen

2. Schritt: Notwendiges Kriterium anwenden

Durch Gleichsetzen von $f‘(x)$ mit Null, erhältst du mögliche Extremstellen. Die Gleichung kannst du ebenfalls mit dem solve-Befehl deines CAS lösen und erhältst dann folgendes Ergebnis:

$x_1 = -1$ , $x_2 = 0$ und $x_3 = 1$

Screenshot eines mathematischen Programms mit Gleichungen und Funktionen zur Ableitung und Lösung.

Abb. 3: Notwendiges Kriterium

3. Schritt: Hinreichendes Kriterium überprüfen

Du hast drei mögliche Extremstellen bestimmt. Setze diese in die zweite Ableitungsfunktion $f‘‘(x)$ ein, um sie zu überprüfen. Du erhältst folgende Ergebnisse:

$f‘‘(-1)= -8$ , Maximalstelle
$f‘‘(0)=4$ , Minimalstelle
$f‘‘(1)= -8$ Maximalstelle

Mathematische Berechnungen in einer Software mit Ableitungen und Werten.

Abb. 4: Hinreichendes Kriterium

4. Schritt: Funktionswerte berechnen

$H_1 (-1 \mid 2)$ $\quad$ $T(0\mid 1)$ $\quad$ $H_2(1\mid 2)$

Der Graph von $f$ besitzt zwei Hochpunkte $H_1 (-1 \mid 2)$ und $H_2(1\mid 2)$ sowie einen Tiefpunkt $T(0\mid 1)$ .

$\blacktriangleright$ Graph zeichnen

$f(-2) = -7$ , $\quad f(2)=-7$

Abb. 5

1.2

$\blacktriangleright$ Flächeninhalt berechnen

Du sollst den Gesamtinhalt der Flächen berechnen, die die Gerade $h$ mit $y=1,5$ mit dem Graphen von $f$ einschließt. Ergänze dazu in deiner Abbildung des Graphen von $f$ die Gerade.

Abb. 6: Eingeschlossene Flächen

1. Schritt: Schnittstellen berechnen

Die Schnittstellen von $f$ und der Gerade $h$ kannst du durch Gleichsetzen der Funktionsterme mit deinem CAS berechnen:

$\begin{array}[t]{rll} f(x)&=&h(x) \\[5pt] f(x)&=& 1,5 \end{array}$

Löse mit dem solve-Befehl. Du erhältst dann folgende Ergebnisse:

$x_1 \approx -1,31$
$x_2 \approx -0,54$
$x_3 \approx 0,54$
$x_4 \approx 1,31$

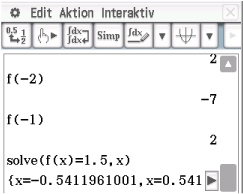Mathematische Software zeigt Funktionen und Lösungen für Gleichungen an.

Abb. 7: Schnittstellen der Funktionen

2. Schritt: Integrale berechnen

Gesucht sind also folgende Integrale:

$A_1 = \left| \displaystyle\int_{-1,3}^{-0,54}(f(x)-h(x))\;\mathrm dx\right|$ und $A_2 = \left| \displaystyle\int_{-0,54}^{0,54}(f(x)-h(x))\;\mathrm dx\right|$

Du kannst die Integrale ebenfalls mit deinem CAS berechnen. Den Befehl findest du unter:

keyboard $\to$ Math2

Du erhältst folgende Ergebnisse:

$A_1 \approx 0,25$
$A_2 \approx 0,35$

Screenshot einer mathematischen Software mit Berechnungen und Integrationen.

Abb. 8: Berechnung der Integrale

Der Gesamtflächeninhalt ergibt sich dann wie folgt:

$\begin{array}[t]{rll} A&=& 2\cdot A_1 + A_2\\[5pt] &\approx& 2\cdot 0,25 + 0,35 \\[5pt] &=& 0,85 \end{array}$

Der Graph von $f$ und die Gerade mit $y =1,5$ schließen Flächen mit einem Gesamtflächeninhalt von ca. $0,85\,\text{[FE]}$ ein.

1.3

$\blacktriangleright$ Schnittwinkel überprüfen

$m_f\cdot m_g = -1$

Berechne also anschließend die Steigungen der beiden Graphen in den Schnittpunkten und überprüfe die Gleichung. Die Steigung eines Graphen wird durch die erste Ableitungsfunktion beschrieben.

1. Schritt: Schnittstellen berechnen

Die Schnittstellen kannst du wie zuvor mit deinem CAS berechnen, indem du $f(x)$ und $g(x)$ gleichsetzt. Du erhältst dann folgendes Ergebnis:

$x_{1,2} =\pm 4\cdot\sqrt{\dfrac{ \sqrt{22.835} + 71}{1.271}}$

2. Schritt: Gleichung überprüfen

Mit deinem CAS kannst du direkt $f‘(x)\cdot g‘(x)$ berechnen.

$f‘(x_1)\cdot g‘(x_1) \approx -7,46 \neq -1$

$f‘(x_2)\cdot g‘(x_2) \approx -7,46 \neq -1$

Die Gleichung ist in den Schnittpunkten also nicht erfüllt. Die Graphen von $f$ und $g$ schneiden sich in keinem Punkt im rechten Winkel.

1.4.1

$\blacktriangleright$ Errichtung eines Zauns überprüfen

1. Schritt: Notwendiges Kriterium anwenden

Da lokale Extremstellen von $g‘$ gesucht sind, musst du $g‘‘(x)=0$ setzen. Dies kannst du wieder mit deinem CAS tun und erhältst folgende Lösungen:

$\begin{array}[t]{rll} g‘‘(x)&=&0 \\[5pt] x_1&=& \dfrac{-4\cdot \sqrt{3}}{3} \\[5pt] x_2&=& \dfrac{4\cdot \sqrt{3}}{3} \end{array}$

Mathematische Berechnungen in einem interaktiven Tool, inklusive Ableitungen und Lösungen.

Abb. 9: Notwendiges Kriterium

2. Schritt: Hinreichendes Kriterium überprüfen

Setze nun $x_1$ und $x_2$ in die dritte Ableitung ein, um die Maximalstelle zu identifizieren. Du erhältst folgendes Ergebnis:

$\begin{array}[t]{rll} g‘‘‘(x_1)&=&g‘‘‘\left(\frac{-4\cdot \sqrt{3}}{3}\right) \\[5pt] &=& \dfrac{9\cdot \sqrt{3} }{40}\gt 0\\[10pt] g‘‘‘(x_2)&=& g‘‘‘\left(\frac{4\cdot \sqrt{3}}{3}\right)\\[5pt] &=& \dfrac{-9\cdot \sqrt{3} }{40}\lt 0 \\[5pt] \end{array}$

An der Stelle $x_2 = \dfrac{4\cdot \sqrt{3} }{3}\approx 2,31$ befindet sich also ein lokales Maximum von $g‘$ .

3. Schritt: Randextrema überprüfen

Berechne nun den Funtionswert $g‘(x)$ , an der lokalen Maximalstelle und den Intervallgrenzen, um die globale Maximalstelle zu bestimmen.

$\begin{array}[t]{rll} g‘(-4)&=& 0 \\[5pt] g‘(4)&=& 0 \\[5pt] g‘\left(\dfrac{4\cdot \sqrt{3}}{3}\right)&=& \dfrac{2\cdot\sqrt{3}}{5} \\[5pt] \end{array}$

Die größte Steigung im betrachteten Intervall hat der Graph von $g$ also an der Stelle $\dfrac{4\cdot \sqrt{3}}{3}$ .

4. Schritt: Steigungswinkel berechnen

Anhand der Steigung $m$ des Graphen von $g$ kannst du nun den Steigungswinkel $\alpha$ an der steilsten Stelle berechnen:

$\tan(\alpha) = m$

$\begin{array}[t]{rll} \tan(\alpha)&=& m \\[5pt] \tan(\alpha)&=& \dfrac{2\cdot\sqrt{3}}{5} \\[5pt] &\approx& 34,7^{\circ} \end{array}$

Vollständige Lösung anzeigen

An der steilsten Stelle fällt die Wand in einem Winkel von ca. $34,7^{\circ}$ . Es muss also ein Zaun errichtet werden.

1.4.2

$\blacktriangleright$ Größe der Abdeckungsfläche berechnen

$s_{f[a;b]}$ $= \displaystyle\int_{a}^{b}\sqrt{1+\left(f‘(x)\right)^2}\;\mathrm dx$

Die Länge der Seite $\overline{AB}$ beträgt $5\,\text{m}$ . Berechne nun die verbleibende Seitenlänge mit Hilfe der Formel.

Setze also in die Formel ein. Das Integral kannst du mit Hilfe des CAS berechnen. Den Befehl dafür findest du unter

keyboard $\to$ Math2

$s_{q[-4;4]} \approx 9,18 \,\text{[m]}$

Vollständige Lösung anzeigen

Mathematische Berechnungen und Funktionalitäten in einer Softwareansicht.

Abb. 10: Integralberechechnung

Die Größe der Fläche der Abdeckung ergibt sich also wie folgt:

$\begin{array}[t]{rll} A&\approx& 5\,\text{m} \cdot 9,18 \,\text{m} \\[5pt] &=& 45,9\,\text{m}^2 \end{array}$

Die Fläche der Abdeckung ist ca. $45,9\,\text{m}^2$ groß.

1.4.3

$\blacktriangleright$ Volumen des Wassers berechnen

Betrachte die Skizze. Die blaue Gerade $h$ modelliert den aktuellen Wasserstand. Einer der Schnittpunkte dieser Gerade mit dem Graphen von $g$ ist $S$ .

Du kannst erkennen, dass sich die Querschnittsfläche aus den beiden roten Flächen und der grünen Fläche zusammensetzt.

Abb. 11: Querschnittsfläche

Da der Graph von $g$ symmetrisch zur $y$ -Achse ist und die roten Flächen Flächen zwischen dem Graphen von $g$ und der $x$ -Achse sind, besitzen die beiden roten Flächen die gleiche Größe $A_1$ . Diese kannst du mit einem Integral mit den Grenzen $-4$ und $x_S$ über $g$ berechnen, wobei $x_S$ die $x$ -Koordinate von $S$ , also die negative Schnittstelle von $g$ und $h$ ist.
Die grüne Fläche ist ein Rechteck, dessen Seitenlängen sich aus dem Betrag der Koordinaten von $S$ ergeben.

Du musst also die Koordinaten von $S$ berechnen, indem du $g(x) =h(x)$ setzt. Dafür benötigst du die Geradengleichung von $h$ . Da $h$ ein Drittel der Beckenhöhe modelliert, musst du zunächst die Tiefe des gesamten Beckens berechnen. Da der Graph von $g$ symmetrisch zur $y$ -Achse ist, liegt der tiefste Punkt genau an der Stelle $x=0$ . Die Tiefe des Beckens ergibt sich also aus dem Funktionswert von $g$ an der Stelle $x=0$ .

1. Schritt: Geradengleichung aufstellen

Berechne die Tiefe des Beckens über $g(0)$ :

$g(0)= -\dfrac{9}{5}$

Vollständige Lösung anzeigen

$h(x)= -\dfrac{6}{5}$

2. Schritt: Koordinaten des Schnittpunkts berechnen

Setze $g(x)=h(x)$ . Die Gleichung kannst du mit dem solve-Befehl deines CAS lösen. Du erhältst folgendes Ergebnis:

$\begin{array}[t]{rll} g(x)&=&h(x) \\[5pt] x_1&=& ... \approx -5,39\\[5pt] x_2&=& ... \approx-1,71 \\[5pt] x_3&=& ... \approx 1,71\\[5pt] x_4&=& ... \approx 5,39 \\[5pt] \end{array}$

Vollständige Lösung anzeigen

$x_1$ und $x_4$ fallen aus der Betrachtung raus, da die Modellierung nur den Bereich $-4 \leq x \leq 4$ betrifft. Der Punkt $S$ aus der Skizze besitzt also folgende Koordinaten $S\left(\frac{-4\cdot \sqrt{-3\cdot \left(\sqrt{6} -3\right)}}{3}\,\bigg \vert \, -\frac{6}{5}\right)$ .

3. Schritt: Größe der Querschnittsfläche berechnen

Die Größe der gesamten Querschnittsfläche $A$ setzt sich wie folgt zusammen:

$A = 2\cdot A_1 + A_2$

$A_2$ kannst du über die Beträge der Koordinaten von $S$ berechnen:

$A_2 \approx 4,11$

Vollständige Lösung anzeigen

$A_1 \approx 1,11$

Vollständige Lösung anzeigen

Insgesamt ergibt sich dann die Größe der Querschnittsfläche wie folgt:

$\begin{array}[t]{rll} A&=& 2\cdot A_1 +A_2 \\[5pt] &\approx& 2\cdot 1,11 + 4,11 \\[5pt] &=& 6,33 \,\left[\text{m}^2\right]\\[5pt] \end{array}$

4. Schritt: Volumen berechnen

Das Becken ist $5\,\text{m}$ lang. Also ergibt sich folgendes Volumen:

$\begin{array}[t]{rll} V&\approx& 6,33 \,\text{m}^2 \cdot 5\,\text{m}\\[5pt] &=& 31,65 \,\text{m}^3\\[5pt] &=& 31.650 \,\text{dm}^3 \\[5pt] &=& 31.650\,l \\[5pt] \end{array}$

Bis das Becken randvoll gefüllt ist, passen noch ca. $31.650\,l$ in das Becken.

Bildnachweise [nach oben]

[1]-[11]