Aufgabe 1 - Analysis
1.1
 Näherungswert für das Integral bestimmen
Näherungswert für das Integral bestimmen
Du sollst in diesem Aufgabenteil das
Integral mit der unteren Integralgrenze

und der oberen Integralgrenze

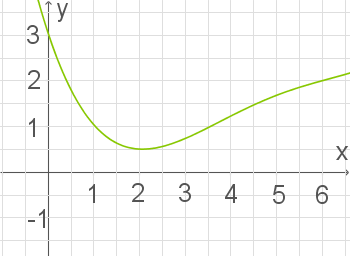
näherungsweise mithilfe der Abbildung bestimmen. Das Integral beschreibt gerade den Flächeninhalt der Fläche, die zwischen dem Graphen der Funktion

und der

-Achse zwischen

und

eingeschlossen wird.
 Lösungsweg A: Kästchen zählen
Lösungsweg A: Kästchen zählen
Zähle also die Kästchen, die sich in diesem Bereich befinden. Dabei entspricht ein Kästchen
 Flächeneinheiten
Flächeneinheiten.
Im Bereich zwischen

und

befinden sich ungefähr

Kästchen. Um nun den Wert des Integrals zu bestimmen, musst du

mit

multiplizieren.

Somit hat das Integral

ungefähr den Wert

 Lösungsweg B: Integral durch Trapez annähern
Lösungsweg B: Integral durch Trapez annähern
Anstatt die Kästchen im Bereich zwischen

und

zu zählen, kannst du die Fläche auch vereinfacht als Trapez betrachten. Der Flächeninhalt

ist durch folgende Formel gegeben:

und

bezeichnen die Längen der parallelen Seiten und

die Höhe des Trapezes.
Folglich gilt für das gesuchte Integral

:
![\(\begin{array}[t]{rll}
I &\approx& \dfrac{f(3)+f(5)}{2} \cdot 2 \\[5pt]
&\approx& \dfrac{0,7 + 1,7}{2} \cdot 2 \\[5pt]
&=& 2,4
\end{array}\)](https://mathjax.schullv.de/229ec4485a47ab74eb3d68468af6f09de347ea33a9674f40f89312423dc8f766?color=5a5a5a)
Somit hat das Integral

mit der Näherung durch ein Trapez ungefähr den Wert

1.2
 Ableitung von
Ableitung von  an der Stelle
an der Stelle  angeben
angeben

ist eine
Stammfunktion der Funktion

, d.h. der Wert von

an der Stelle

gibt gerade die Ableitung von

an der Stelle

an. Du musst also den Wert

in der Abbildung ablesen.

Demnach ist die Ableitung der Funktion

an der Stelle

ungefähr

.
1.3
 Wert des Integrals berechnen
Wert des Integrals berechnen
Wenn du ein Integral

gegeben hast, gilt nach dem
Hauptsatz der Differential- und Integralrechnung

bezeichnet dabei eine Stammfunktion von

.
Nach Voraussetzung ist

, sodass für das Integral

gilt:
![\(\begin{array}[t]{rll}
\displaystyle\int_3^b f(x) \;\mathrm dx &=& F(b) - F(3) \\[5pt]
&=& F(b) - 0 \\[5pt]
&=& F(b)
\end{array}\)](https://mathjax.schullv.de/3bc8e3adaaecf0f299532102cad8844af1c2cc6c82a6fd7a5e4068649c7627b5?color=5a5a5a)
Demnach ist der Wert des Integrals

für beliebige

gleich

.
Aufgabe 2 - Analysis
2.1
 Gültigkeit der Gleichung zur Beschreibung von
Gültigkeit der Gleichung zur Beschreibung von  für jeden Wert von
für jeden Wert von  nachweisen
nachweisen
Eine Tangente ist eine Gerade und kann immer durch eine Steigung des Graphen

und einen

-Achsenabschnitt beschrieben werden. Um zu zeigen, dass die in der Aufgabenstellung gegebene Tangente der Tangente an der Stelle

entspricht, musst du nachweisen, dass die Steigung der gegebenen Tangente der Steigung an der Stelle

entspricht und, dass eine Gerade durch den Punkt

mit dieser Steigung den

-Achsenabschnitt

hat.
1.Schritt: Steigung bestimmen
Um die Steigung an der Stelle

zu bestimmen, leitest du die Funktion zunächst ab. Danach setzt du

ein.
![\(\begin{array}[t]{rll}
f_a(x) &=& a \cdot e^{a+x} &\quad \scriptsize \; \\[5pt]
f_a](https://mathjax.schullv.de/fcdb0ba855643a8b525c7d7fbb644e2cb8e1971489e97c7378aae311161a14ba?color=5a5a5a)
Die Steigung entspricht der Steigung der gegebenen Tangente.
2. Schritt:  -Achsenabschnitt überprüfen
-Achsenabschnitt überprüfen
Um zu überprüfen, ob der in der Aufgabenstellung gegebene

-Achsenabschnitt richtig ist, setzt du die Koordinaten des Punkts

in die gegebene Tangentengleichung ein. Entspricht dies einer wahren Aussage, ist der

-Achsenabschnitt korrekt gewählt.
Der in der Aufgabenstellung gegebene

-Achsenabschnitt ist richtig. Damit wird die Tangente am Punkt

durch die Gleichung

beschrieben.
2.2
 Flächeninhalt des Dreiecks in Abhängigkeit von
Flächeninhalt des Dreiecks in Abhängigkeit von  berechnen
berechnen
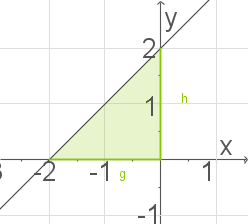 Abb. 1: Dreieck mit
Abb. 1: Dreieck mit 
Um den Flächeninhalt des beschriebenen Dreiecks zu berechnen, benötigst du die Länge

der Grundseite und die Höhe

des Dreiecks. Die Länge der Grundseite entspricht dem Abstand der Nullstelle zum Ursprung.
Die Höhe entspricht dem in der Tangentengleichung gegebenen

-Achsenabschnitt

. Zur Bestimmung der Länge

der Grundseite bestimmst du zunächst die Nullstelle der Tangente:
Die Nullstelle der Tangente ist unabhänig von

immer bei

. Damit ist die Länge der Grundseite des Dreiecks gleich 2.
Der Flächeninhalt des Dreiecks ist somit:
![\(\begin{array}[t]{rll}
A &=& \dfrac{g \cdot h}{2} &\quad \scriptsize \\[5pt]
A &=& \dfrac{2 \cdot 2 \cdot a \cdot e^{a-1}}{2} &\quad \scriptsize \\[5pt]
A &=& 2 \cdot a \cdot e^{a-1} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d84c7a49e8ddf69e603c74c381d4f63abf11bee56dc0159a1a94ac6eacf51bfb?color=5a5a5a)
Der Flächeninhalt des Dreiecks beträgt

.
Aufgabe 3 - Analytische Geometrie
3.1
 Koordinatenachsen zeichnen
Koordinatenachsen zeichnen
Der Punkt

hat die Koordinaten

, d.h. der
Ursprung des Koordinatensystems liegt in

. Da der Punkt

als erste Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die

-Achse die Gerade

. Die Richtung der

-Achse ist dabei die Richtung des Vektors

. Das Vorgehen bei der

-Achse ist analog. Da der Punkt

als zweite Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die

-Achse die Gerade

. Die Richtung der

-Achse ist dabei die Richtung des Vektors

. Der Punkt

hat als letzte Koordinate eine negative Zahl (die restlichen Koordinaten sind gleich Null), das bedeutet, dass die

-Achse die Gerade

ist. Die Richtung ist dieses Mal allerdings die Richtung des Vektors

.
Somit ergibt sich folgendes Koordinatensystem:
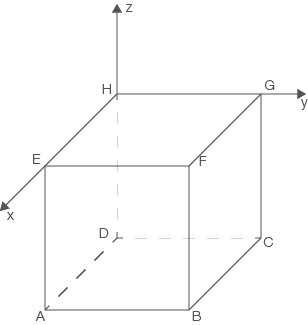 Abb. 2: Würfel im Koordinatensystem
Abb. 2: Würfel im Koordinatensystem
Der Punkt

hat demnach die Koordinaten

3.2
 Punkt
Punkt  bestimmen
bestimmen
Sind zwei Punkte

und

gegeben, so ist der
Abstand 
der beiden Punkte definiert als
Der Punkt

soll auf der Kante

des Würfels liegen und soll zum Punkt

(dem Ursprung des Koordinatensystems) den Abstand

haben, d.h.

. Die Koordinaten des zweiten Punkts

sind gegeben. Die Koordinaten des ersten Punkts

kannst du mithilfe des Ortvektors von

und dem Vektor

umschreiben.

mit

Setze nun die Koordinaten der Punkte in die Formel für den Abstand mit

ein und löse die Gleichung nach

auf
Da für

der Punkt

nicht auf der Kante

liegen würde, muss

sein. Für

gilt somit

Somit sind die Koordinaten von

Aufgabe 4 - Stochastik
4.1
 Begründen, dass es sich nicht um ein Laplace-Experiment handelt
Begründen, dass es sich nicht um ein Laplace-Experiment handelt
Du sollst begründen, dass es sich bei dem beschriebenen Münzwurf nicht um ein
Laplace-Experiment handelt. Ein Laplace-Experiment liegt vor, wenn folgende Bedingungen erfüllt sind:
- Es gibt nur endlich viele Ergebnisse.
- Jedes Ergebnis hat die gleiche Wahrscheinlichkeit.
Da die Ergebnismenge angegeben ist, weißt du, dass die erste Bedingung erfüllt ist. Es kann also nur an der zweiten liegen. Betrachtest du die Ergebnismenge genauer, siehst du, dass es Ergebnisse gibt, bei denen die Münze nur zweimal geworfen werden muss, und Ergebnisse, bei denen die Münze dreimal geworfen wird. Für erstere ist die Wahrscheinlichkeit jeweils

, während sie für letztere jeweils

beträgt. Also kann es sich nicht um ein Laplace-Experiment handeln.
4.2
 Erwartungswert berechnen
Erwartungswert berechnen
Den Erwartungswert

einer Zufallsvariable

mit den möglichen Ergebnissen

bis

berechnest du mit folgender Formel:
Da

die Anzahl der Münzwürfe beschreibt, gibt es nur die beiden Möglichkeiten

und

, welche jeweils die Wahrscheinlichkeit

bzw.

haben. Also ergibt sich folgender Erwartungswert:
Der Erwartungswert von

beträgt

.
 .
.
 an der Stelle 2 an.
an der Stelle 2 an.
 mit
mit  gilt.
gilt.
 die Tangente
die Tangente  durch die Gleichung
durch die Gleichung  beschrieben werden kann.
beschrieben werden kann.
 schließen die Tangente
schließen die Tangente  und die beiden Koordinatenachsen ein Dreieck ein.
Ermittle den Flächeninhalt dieses Dreiecks in Abhängigkeit von
und die beiden Koordinatenachsen ein Dreieck ein.
Ermittle den Flächeninhalt dieses Dreiecks in Abhängigkeit von  .
.
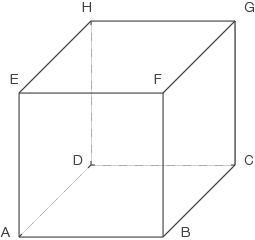
 . Die Eckpunkte
. Die Eckpunkte  ,
,  ,
,  und
und  dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten:
dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten:  ,
,  ,
,  und
und  .
.
 an.
an.
 liegt auf der Kante
liegt auf der Kante  des Würfels und hat vom Punkt
des Würfels und hat vom Punkt  den Abstand
den Abstand  .
Berechne die Koordinaten des Punktes
.
Berechne die Koordinaten des Punktes  .
.
 ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu.
ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu.
 .
.
 Abb. 2: Würfel im Koordinatensystem
Abb. 2: Würfel im Koordinatensystem