3 Analytische Geometrie – Wahlaufgabe

Der Sockel eines Pokals aus Glas kann durch einen geraden, quadratischen Pyramidenstumpf beschrieben werden. Die Eckpunkte dieses Pyramidenstumpfes haben in einem Koordinatensystem folgende Koordinaten:

$A(4\mid 4\mid 0),$ $B(-4\mid4\mid 0),$ $C(-4\mid-4\mid 0)$ und $D(4\mid-4\mid 0)$ sowie $E(2\mid 2\mid 6),$ $F(-2\mid2\mid 6),$ $G(-2\mid-2\mid 6)$ und $H(2\mid-2\mid 6).$

Eine Längeneinheit entspricht einem Zentimeter.

3.1

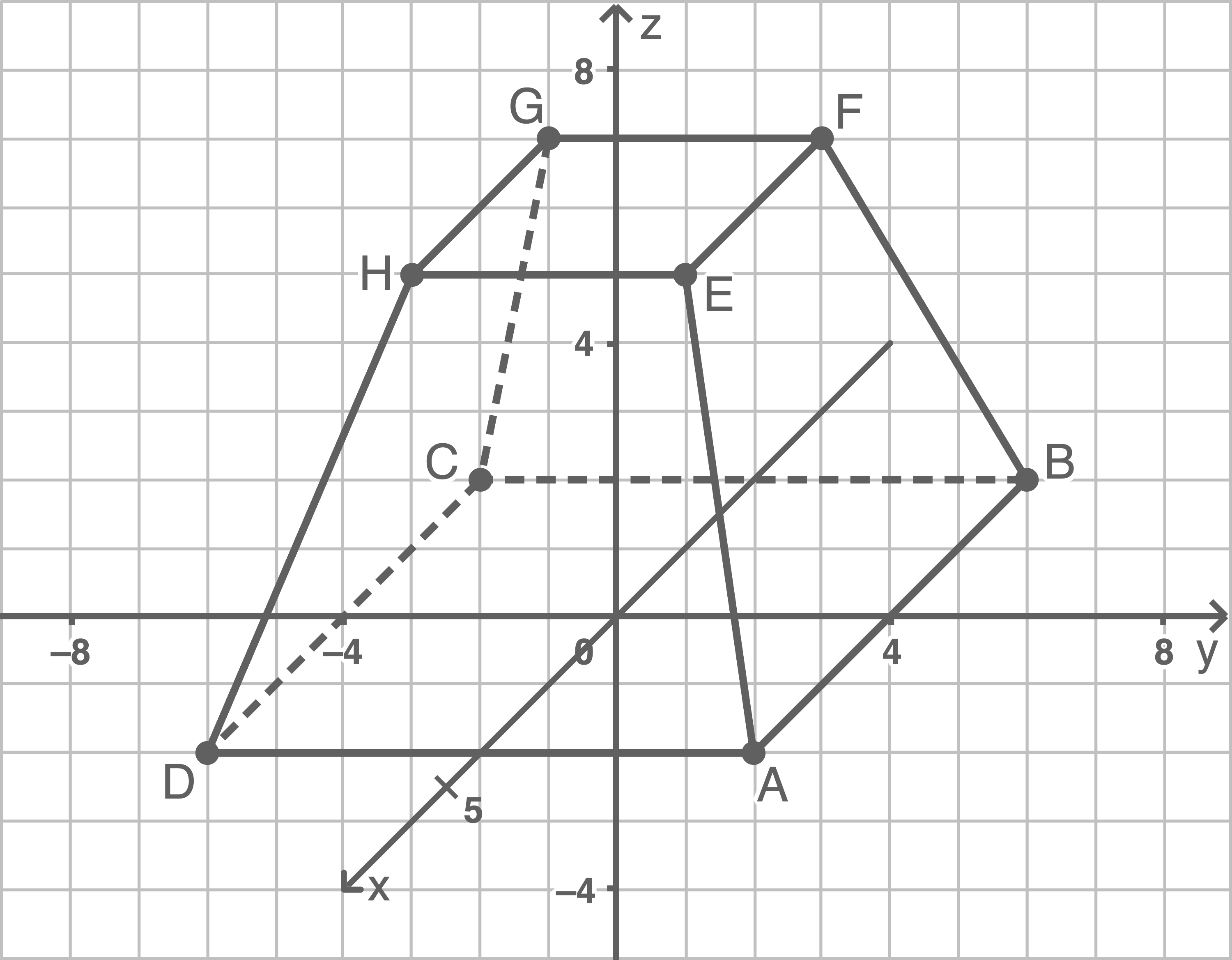
Stelle den Pyramidenstumpf in einem Koordinatensystem graphisch dar.

(4 BE)

3.2

Nenne die Anzahl der Symmetrieebenen, die dieser Pyramidenstumpf besitzt.

Gib für eine dieser Ebenen eine Gleichung an.

(2 BE)

3.3

Das Glas, aus dem der Sockel hergestellt wurde, hat die Dichte $\rho=2,51 \dfrac{\mathrm{g}}{\mathrm{cm}^3}.$

Ermittle die Masse des Sockels.

(5 BE)

3.4

Ermittle eine Koordinatengleichung der Ebene, in der die Punkte $A, B$ und $E$ liegen.

$\left[ \text{zur Kontrolle}: \; 3 y+z-12=0 \right]$

(3 BE)

3.5

Bestimme die Größe des Neigungswinkels einer Seitenfläche zur Grundfläche des Sockels.

(3 BE)

3.6

Ein Laserstrahl trifft auf eine Seitenfläche des Sockels auf, geht durch ihn hindurch und verlässt den Sockel durch eine andere Begrenzungsfläche. Der Eintrittsort entspricht dem Punkt $P(-1\mid-2,5\mid 4,5)$ in der Seitenfläche $CDHG$ des Pyramidenstumpfes und die Richtung des Laserstrahls im Glaskörper dem Vektor $\overrightarrow{v}=\left(\begin{array}{r}-1 \\ 2 \\ -1\end{array}\right)$ .

Der Austrittspunkt des Laserstrahls aus dem Körper soll bestimmt werden. Kim hat dafür den folgenden Lösungsweg mit den Schritten (1) bis (6) gewählt.

$(1)$

$g: \overrightarrow{x}=\pmatrix{-1\\-2,5\\4,5}+r\cdot \pmatrix{-1\\2\\-1}$ mit $r\in\mathbb{R}$

$(2)$

$4,5+r \cdot(-1)=0 \Leftrightarrow r=4,5$

$(3)$

$\mathrm{S}_{x y}(-5,5\mid 6,5\mid 0)$

$(4)$

$y=6,5>4 \Rightarrow g$ schneidet $A B F E$

$(5)$

$3(2 r-2,5)+(4,5-r)=12 \Leftrightarrow r=3$

$(6)$

$Q(-4\mid 3,5\mid 1,5)$

Die Vorgehensweise beinhaltet einen Denkfehler.

Erkläre den Fehler.

(5 BE)

3.7

Auf dem Sockel soll eine gerade Linie eingraviert werden. Diese Linie entspricht der Strecke zwischen den Mittelpunkten der Körperkanten $\overline{AB}$ und $\overline{EF}.$

Zur Gravur wird ein vertikal beweglicher Laser verwendet. Im Modell wird der Austrittspunkt des Laserstrahls aus dem Laser durch den Punkt $Q_z(0\mid 7\mid z)$ mit $1 \leq z \leq z_\text{max}$ beschrieben.

Der Laserstrahl trifft immer senkrecht auf die zu gravierende Fläche auf.

Bestimme $z_\text{max}.$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

Sockel Pokal MV Mathe Abi 2024 Pyramidenstumpf

3.2

Die Symmetrieebenen des Pyramidenstumpfs stehen senkrecht zur $xy$ -Ebene des Koordinatensystems und enthalten entweder je zwei gegenüberliegende Eckpunkte der Grund- bzw. Deckfläche oder die Mittelpunkte der parallel zueinander verlaufenden Kanten der Grund- bzw. Deckfläche des Pyramidenstumpfes.

Es gibt somit vier mögliche Symmetrieebenen.

Mögliche Ebenengleichungen sind $y=0,\;$ $x=0,\;$ $x+y=0$ sowie $x-y=0.$

3.3

1. Schritt: Volumen bestimmen

Der Pyramidenstumpf kann durch Aufsetzen einer kleinen Pyramide zu einer großen Pyramide ergänzt werden.

Mit dem zweiten Strahlensatz gilt, dass das Längenverhältnis der parallelen Strecken gleich dem Längenverhältnis der Strecken auf einem Schenkel ist.

Da für die parallelen Kanten des Pyramidenstumpfes $|\overline{AB}|=2 \cdot|\overline{EF}|$ gilt, gilt für das Verhältnis der Schenkel und somit für die Höhe der Pyramide:

$\begin{array}[t]{rll} h_{\text {Pyr }}&=& 2 \cdot h_{\text {Stumpf }}&\\[5pt] &=& 2\cdot 6 &\\[5pt] &=& 12 \end{array}$

Somit folgt für das Volumen des Pyramidenstumpfs:

$\begin{array}[t]{rll} V_{\text {Stumpf }}&=& V_{\text {Pgroß }}-V_{\text {Pklein }}& \\[5pt] &=&\dfrac{1}{3} \cdot 8^2 \cdot 12-\dfrac{1}{3} \cdot 4^2 \cdot 6 & \\[5pt] &=& 224 & \\[5pt] \end{array}$

2. Schritt: Masse berechnen

$\begin{array}[t]{rll} m&=&\rho \cdot V & \\[5pt] &=& 2,51\; \dfrac{\text{g} }{\text{cm}^{3} } \cdot 224 \mathrm{~cm}^3& \\[5pt] &\approx& 562\,\text{g} \end{array}$

3.4

Es gilt:

$\overrightarrow{AB}=\pmatrix{-4\\4\\0}-\pmatrix{4\\4\\0}=\pmatrix{-8\\0\\0}$

$\overrightarrow{AE}=\pmatrix{2\\2\\6}-\pmatrix{4\\4\\0}=\pmatrix{-2\\-2\\6}$

Ein Normalenvektor der Ebene, in der die Punkte $A,B$ und $E$ liegen, ergibt sich aus dem Kreuzprodukt zweier Vektoren, die die Ebene aufspannen:

$\begin{array}[t]{rll} \overrightarrow{n}&=& \overrightarrow{AB} \times \overrightarrow{AE} & \\[5pt] &=& \pmatrix{-8\\0\\0} \times \pmatrix{-2\\-2\\6} & \\[5pt] &=& \pmatrix{0\cdot 6-0\cdot (-2)\\0\cdot (-2)-(-8)\cdot 6\\(-8)\cdot (-2)-0\cdot (-2)}& \\[5pt] &=& \pmatrix{0\\48\\16} & \\[5pt] &=& 16\cdot \pmatrix{0\\3\\1} \end{array}$

Einsetzen des gekürzten Normalenvektors in die allgemeine Koordinatengleichung liefert:

$\begin{array}[t]{rll} E: 0\cdot x+3\cdot y+1\cdot z&=& d& \\[5pt] 3y+z&=& d \end{array}$

Einsetzen der Koordinaten von $A$ ergibt nun:

$\begin{array}[t]{rll} E: 3\cdot 4+0&=& d& \\[5pt] 12&=& d \end{array}$

Eine Ebenengleichung ist somit gegeben durch:

$\begin{array}[t]{rrl} E: & 3y+z &=& 12 &\quad \scriptsize \mid\; -12\\[5pt] & 3y+z-12&=& 0 \end{array}$

3.5

Da es sich um einen geraden, quadratischen Pyramidenstumpf handelt, sind die Neigungswinkel für alle Seitenflächen gleich groß.

Die Seitenfläche $ABFE$ hat den Normalenvektor $\overrightarrow{n_1}=\pmatrix{0\\3\\1}.$ Die Grundfläche liegt in der $xy$ -Ebene und besitzt somit den Normalenvektor $\overrightarrow{n_2}=\pmatrix{0\\0\\1}.$

Für den Neigungswinkel gilt also:

Rechenweg anzeigen

$\alpha \approx 71,6^\circ$

Der Neigungswinkel einer Seitenfläche zur Grundfläche des Sockels beträgt somit etwa $71,6^\circ .$

3.6

In den Schritten $(1)$ bis $(3)$ ermittelt Kim die Koordinaten des Punktes, in dem die Laserstrahlgerade auf die $xy$ -Ebene des Koordinatensystems trifft, in der die Grundfläche $ABCD$ liegt.

In Schritt $(4)$ folgt aus $y=6,5\gt 4,$ dass der Austrittspunkt des Laserstrahls aus dem Körper außerhalb der Grundfläche liegt, da für diese $-4 \leq y \leq 4$ gilt.

Kim schlussfolgert alternativlos, dass der Austrittspunkt in der Seitenfläche $ABFE$ liegen muss, und berechnet in Schritt $(5)$ mit Hilfe der Ebenengleichung aus Aufgabe 3.4 die Koordinaten des Schnittpunktes $Q$ des Laserstrahls, der entlang der Gerade $g$ verläuft, mit der Seitenfläche $ABFE.$

Die berechneten Koordinaten widerlegen Kims Annahme zur Lage des Austrittspunkts, da der berechnete Punkt mit $x_Q=-4$ und $z_Q \gt 0$ außerhalb der Fläche $ABFE$ liegt.

Es wären daher noch weitere Überlegungen zur Lage des Austrittspunkts und das Überprüfen der weiteren Seitenflächen erforderlich.

3.7

Da der Laser vertikal beweglich ist und der Austrittspunkt durch den Punkt $Q_z(0\mid 7\mid z)$ mit $1 \leq z \leq z_{max}$ beschrieben wird, ergibt sich ein Zusammenhang wie in folgenden Abbildungen dargestellt:

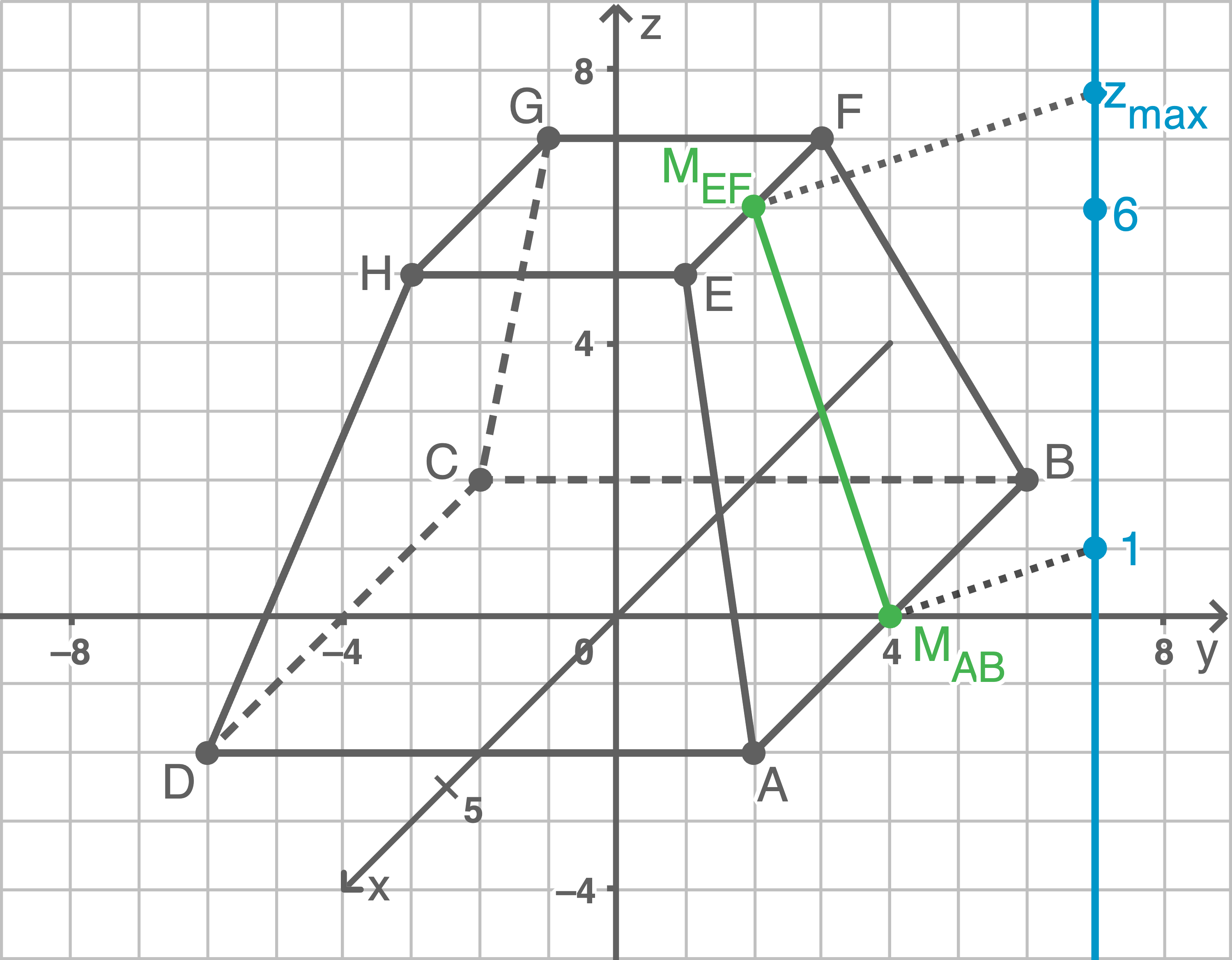
Laserstrahlen Stadtplan Grundriss Hessen Mathe Abi 2014

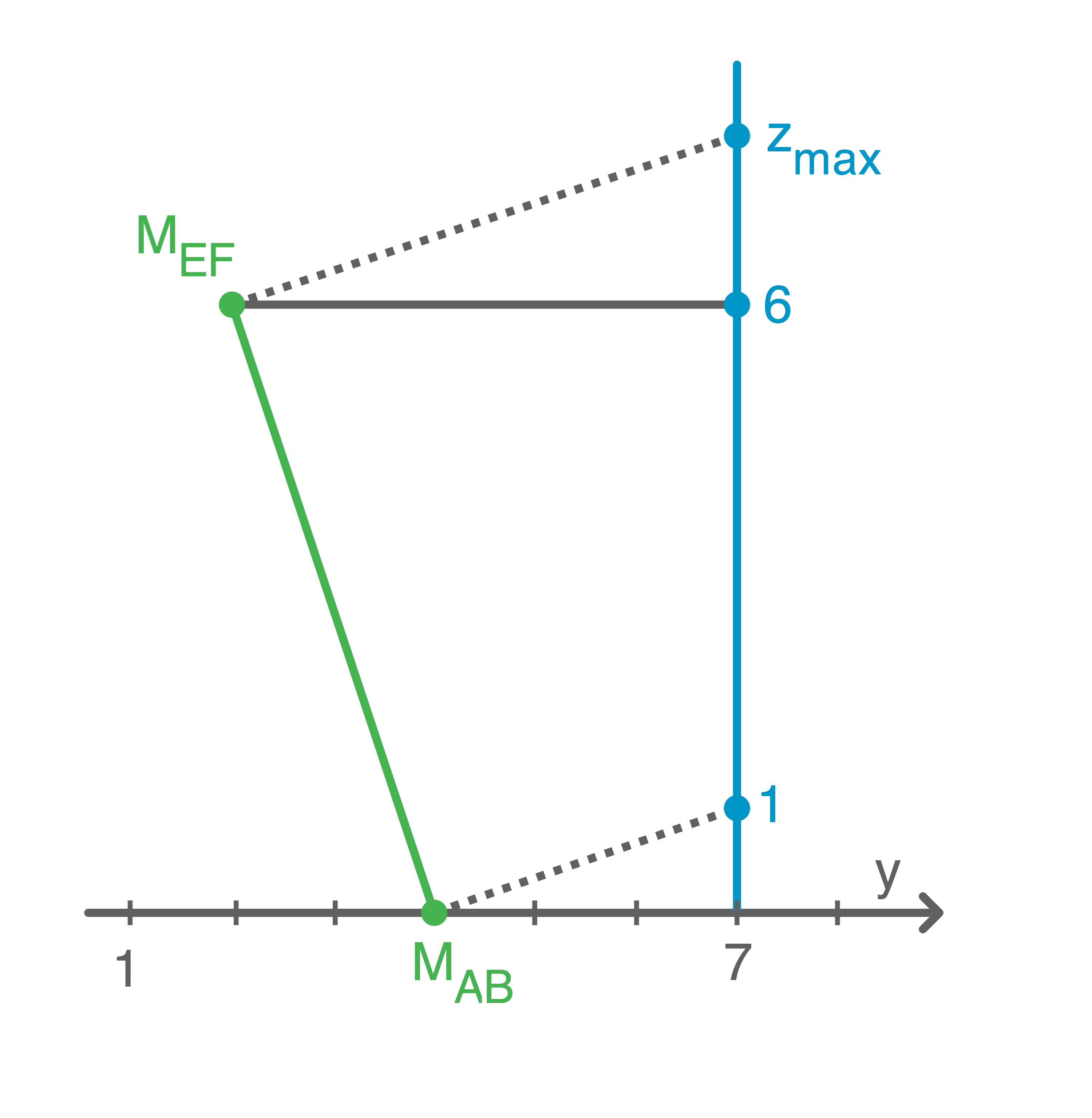Der Schnitt durch die Mittelpunkte der Kanten $\overline{AB}$ und $\overline{EF}$ verläuft in der $yz$ -Ebene. Für die Mittelpunkte gilt:

Für $M_{AB}: \; y=4$

Für $M_{EF}: \; y=2$

Da der Laser immer senkrecht auftritt, sind die Winkel der beiden Dreiecke jeweils gleich groß und die Dreiecke somit ähnlich zueinander.

Aus der Dreiecksähnlichkeit folgt, dass die Verhältnisse entsprechender Seiten gleich sind. Somit gilt:

$\begin{array}[t]{rll} \dfrac{z_{\text{max} }-6}{7-2}&=& \dfrac{1}{7-4}&\quad \scriptsize \mid\; \cdot 5 \\[5pt] z_{\text{max} }-6&=& \dfrac{5}{3}&\quad \scriptsize \mid\; +6 \\[5pt] z_{\text{max} }&=& \dfrac{5}{3}+6 & \\[5pt] z_{\text{max} }&=& \dfrac{23}{3} \end{array}$

Alternativer Lösungsweg:

Die Ebene, in der die Seitenfläche $ABFE$ liegt, hat den Normalenvektor $\overrightarrow{n}=\pmatrix{0\\3\\1}.$

Die Geraden $\overrightarrow{x}= \pmatrix{0\\7\\z} +r\cdot \pmatrix{0\\3\\1}$ beschreiben somit die möglichen Verläufe des Laserstrahls.

Der Punkt auf der zu gravierenden Strecke, der die größte $z$ -Koordinate besitzt, ist $M_{EF}(0 \mid 2\mid 6).$

Es gilt also:

$\pmatrix{0\\7\\z_{\text{max}}}+r\cdot \pmatrix{0\\3\\1}=\pmatrix{0\\2\\6}$

Aus der zweiten Zeile ergibt sich:

$\begin{array}[t]{rll} 7+r\cdot 3&=& 2 &\quad \scriptsize \mid\; -7\\[5pt] r\cdot 3&=& -5 &\quad \scriptsize \mid\; :3\\[5pt] r&=& -\dfrac{5}{3} \end{array}$

Der Wert von $z_{\text{max}}$ folgt also mit:

$\begin{array}[t]{rll} z_{\text{max}} +r\cdot 1 &=& 6 &\quad \scriptsize \,\bigg \vert \, \; r=-\dfrac{5}{3} \\[5pt] z_{\text{max}} -\dfrac{5}{3} &=& 6 &\quad \scriptsize \,\bigg \vert \, \; +\dfrac{5}{3} \\[5pt] z_{\text{max}}&=& \dfrac{23}{3} \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?