Stochastik

Ein Unternehmen produziert Stahlkugeln für Kugellager. Erfahrungsgemäß sind $4\;\%$ aller Kugeln fehlerhaft. $800$ Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße beschrieben werden.

3.1

Bestimme die Wahrscheinlichkeit dafür, dass unter den ausgewählten Kugeln weniger als $30$ fehlerhaft sind.

(2 BE)

3.2

Bestimme die Wahrscheinlichkeit dafür, dass die Anzahl der fehlerhaften Kugeln unter den ausgewählten höchstens um eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht.

(5 BE)

3.3

Eine fehlerhafte Kugel hat entweder einen Formfehler oder einen Größenfehler. Die Wahrscheinlichkeit dafür, dass eine Kugel einen Formfehler hat, beträgt $3\;\%$ .
Alle Kugeln werden vor dem Verpacken geprüft. Dabei werden $95\;\%$ der Kugeln mit Formfehler, $98\;\%$ mit Größenfehler, aber auch $0,5\;\%$ der Kugeln ohne Fehler aussortiert.

3.3.1

Stelle den Sachzusammenhang in einem beschrifteten Baumdiagramm dar.

(4 BE)

3.3.2

Berechne die Wahrscheinlichkeit dafür, dass eine aussortierte Kugel keinen Formfehler hat.

(3 BE)

3.4

Die Masse der hergestellten Kugeln hat einen Sollwert von $2\,\text{g}$ pro Stück. Produktionsbedingt streut die Masse der Kugeln geringfügig um den Sollwert. Kugeln mit Formfehler und fehlerlose Kugeln haben keine Masseabweichung. Weicht die Masse der Kugel um mehr als $5\;\%$ vom Sollwert ab, so liegt ein Größenfehler vor.

Es werden Packungen mit je fünf Kugeln ausgeliefert. Die Kugeln von zwei zufälig ausgewählten Packungen wurden bezüglich ihrer Masse untersucht und die Messwerte notiert.

Packung	$1$
Kugel 1	$2,00 \; \text{g}$
Kugel 2	$2,01 \; \text{g}$
Kugel 3	$2,00 \; \text{g}$
Kugel 4	$1,98 \; \text{g}$
Kugel 5	$2,02 \; \text{g}$

3.4.1

Bestimme für die Masse der Kugeln von Packung $1$ das arithmetische Mittel $\overline{x}$ .

(1 BE)

3.4.2

Das arithmetische Mittel der Kugelmassen einer weiteren Packung $2$ sitmmt mit dem der Kugelmassen der Packung $1$ überein. Die Standardabweichung der Kugelmassen der Packung $2$ ist größer als die von Packung $1$ .

Triff eine Aussage über die Masse der Kugeln aus Packung $1$ im Vergleich zu denen der Packung $2$ . Begründe deine Aussage.

(3 BE)

3.4.3

Die mittlere Abweichung $d_{\overline{x}}$ ist ein weiteres Streuungsmaß und kann mit der Gleichung $d_{\overline{x}} = ...$

Gleichung anzeigen

berechnet werden.

Berechne $d_{\overline{x}}$ für die Kugelpackung $1$ .
Interpretiere das Ergebnis im Sachzusammenhang.

(3 BE)

3.4.4

Betrachtet wird eine beliebige Messreihe mit den Ergebnissen $x_1$ bis $x_n$ und dem arithmetischen Mittel $\overline{x}$ .

Bestimme den Wert des Terms $\dfrac{ \overline{x}-x_1 + \overline{x}-x_2 +\ldots+ \overline{x}-x_n }{n}$ , $n \in \mathbb{N}$ , $n\geq1$ .

Begründe, dass der Wert dieses Terms als Streuungsmaß ungeeignet ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

Sei X die Anzahl der fehlerhaften Kugeln. X ist $B_{800; \; 0,04}$ verteilt. Mit dem Taschenrechner folgt:

$P_{0,04}^{800}(X \lt 30) = P_{0,04}^{800}(X \leq 29) \approx 0,33$

Die Wahrscheinlichkeit, dass unter den ausgewählten Kugeln weniger als 30 Kugeln fehlerhaft sind, beträgt etwa $33 \; \%.$

3.2

Sei X die Anzahl der fehlerhaften Kugeln. X ist $B_{800; \; 0,04}$ verteilt.

1. Schritt: Erwartungswert und halbe Standardabweichung bestimmen
Der Erwartungswert lässt sich wie folgt berechnen.

$E(X) = n \cdot p= 800 \cdot0,04=32$

Für die halbe Standardabweichung gilt:

$\sigma = 0,5 \cdot \sqrt{n \cdot p \cdot (1-p)} \approx 2,8$

2. Schritt: Wahrscheinlichkeit bestimmen
Da die Anzahl $X$ der fehlerhaften Kugeln höchstens um eine halbe Standardabweichung vom Erwartungswert abweichen darf, muss $30 \leq X \leq 34$ gelten. Mit dem Taschenrechner folgt:

$P_{0,04}^{800}(30\leq X\leq34)$ $= P_{0,04}^{800}( X\leq 34) - P_{0,04}^{800}( X \leq30) \approx 0,35$

Die Wahrscheinlichkeit für das gegebene Ereignis beträgt etwa $35 \; \%.$

3.3.1

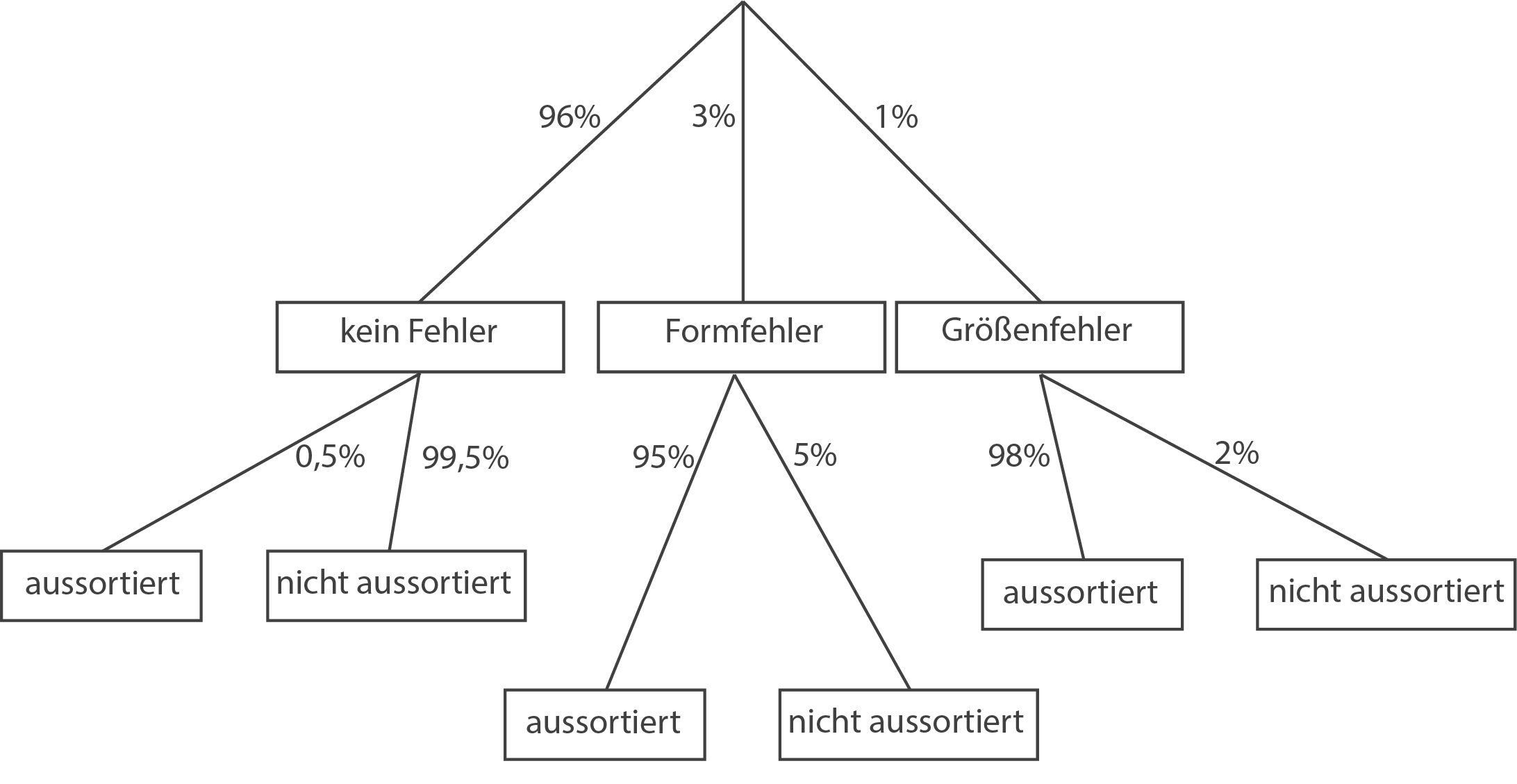
Diagramm zur Fehleranalyse mit Kategorien und Prozentangaben.

3.3.2

$\dfrac{P(\text{Aussortierte Kugel, keinen Formfehler)}}{\text{P(Aussortierte Kugel)}}$ $= \dfrac{0,01 \cdot 0,98+0,96 \cdot 0,005}{0,03 \cdot 0,95+0,01\cdot0,98+0,96\cdot0,005}$ $\approx 0,34$

Die Wahrscheinlichkeit, dass eine aussortierte Kugel keinen Formfehler hat, beträgt etwa $34 \; \%.$

3.4.1

$\overline{x}=\dfrac{2+2,01+2+1,98+2,02}{5}\,g=2,002\,g$

3.4.2

Das arithmetische Mittel ist lediglich der Durchschnittswert über die Masse aller Kugeln. Die Standardabweichung gibt das Maß der Streuung an.
Die größere Streuung der Kugelmassen in Packung $2,$ bedeutet, dass die Masse einzelner Kugeln dort weiter vom Sollwert abweichen kann.

3.4.3

Vollständigen Rechenweg anzeigen

$d_{\overline{x}} = 0,0104$

Durch $d_{\overline{x}}$ wird die durchschnittliche betragsmäßige Abweichung vom arithmetischen Mittel angegeben. Diese beträgt bei Packung $1$ etwa $0,0104 \; \text{g}.$

3.4.4

$\begin{array}[t]{rll} & & \dfrac{\overline{x}-x_1+\overline{x}-x_2 +\ldots +\overline{x}-x_n}{n} & \quad \scriptsize \\[5pt] &=&\dfrac{n \cdot \overline{x} - \left(x_1+x_2 +\ldots + x_n\right)}{n} & \quad \scriptsize \\[5pt] &=&\dfrac{n \cdot \overline{x}}{n}-\dfrac{x_1+x_2+ \ldots +x_n}{n} & \quad \scriptsize \\[5pt] &=&\overline{x}-\overline{x} & \quad \scriptsize \\[5pt] &=& 0 & \quad \scriptsize \\[5pt] \end{array}$

Der Term kann nicht zur Beschreibung der Streuung verwendet werden, weil er immer $0$ ergibt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?