Analytische Geometrie
6
Betrachtet wird die Schar der Ebenen 
mit 
Die Abbildung zeigt die Gerade 
die in der 
-Ebene liegt.
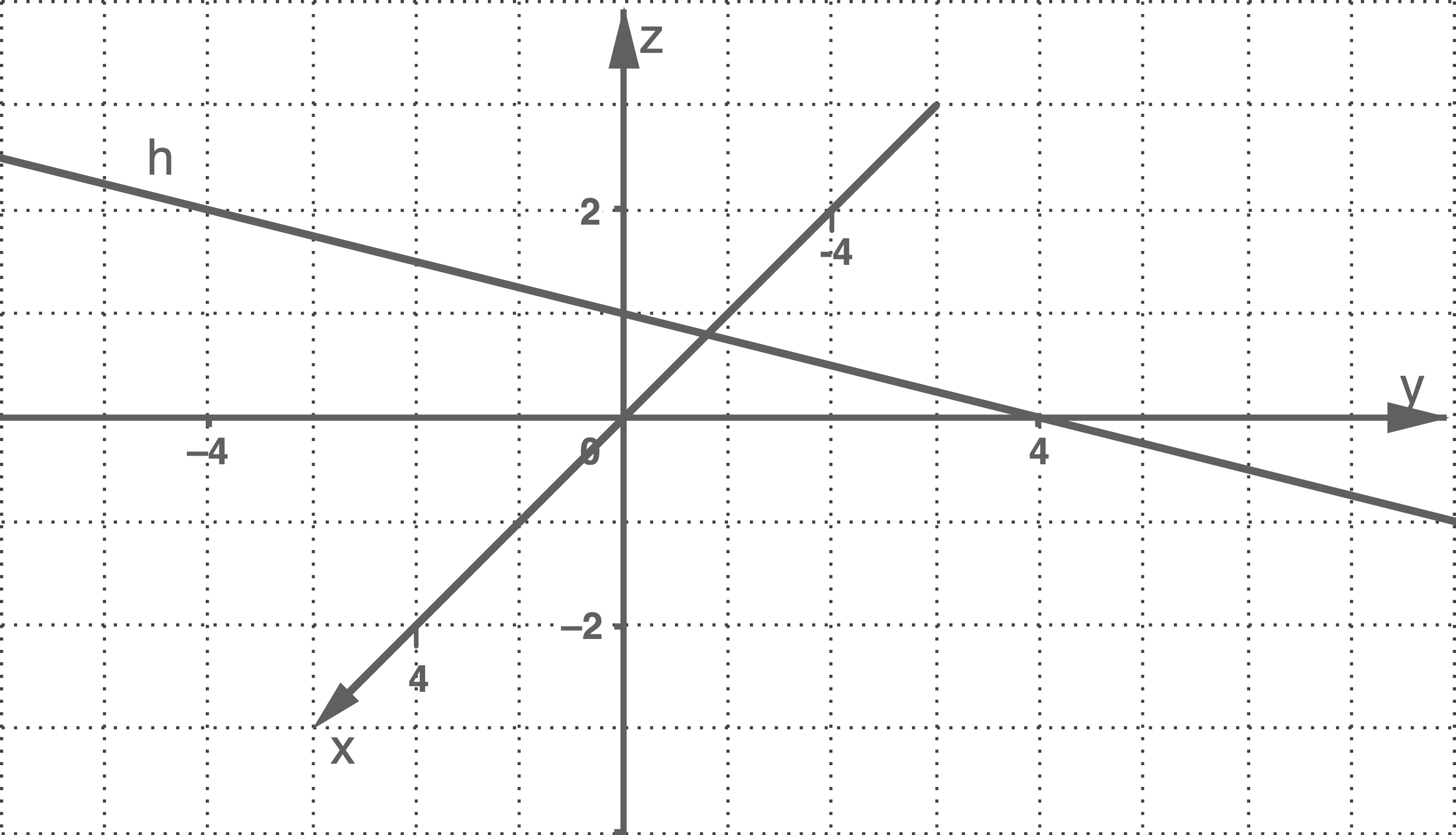
6.1
Begründe, dass alle Ebenen der Schar die Gerade 
enthalten.
(2 BE)
6.2
Der Vektor 
ist ein Richtungsvektor einer Ebene der Schar. Diese Ebene wird mit 
bezeichnet. Beurteile die folgende Aussage:
Würde man in der Abbildung darstellen, so würde die Darstellung von mit der Darstellung von übereinstimmen.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
6.1
Aufgrund der speziellen Lage lassen sich aus der grafischen Darstellung für die Gerade die Koordinaten zweier Punkte ablesen: 
und 
Die Punktproben von 
und 
mit 
ergeben jeweils wahre Aussagen, somit liegt in allen Ebenen der Schar:
in 
also 
in 
also
6.2
Die Gerade liegt laut Aussage in 6.1 in der Ebene 
Alle weiteren Punkte von ergeben sich geometrisch durch Antragen eines beliebigen Vielfachen des Richtungsvektors an die Punkte der Geraden 
Da beim Antragen des Vektors in der gegebenen zweidimensionalen Darstellung alle Punkte der Geraden wieder auf sich selbst abbildet werden, stimmt die Aussage.