1.1
 Symmetrie bestimmen
Symmetrie bestimmen
Der Graph einer Funktion kann verschiedene Symmetrien aufweisen. Er kann zum Beispiel punktsymmetrisch zum Ursprung oder achsensymmetrisch zur

-Achse sein. Bei ganzrationalen Funktionen kann die Art der Symmetrie an den Exponenten abgelesen werden.
Kommen nur gerade Exponenten vor, ist der Graph achsensymmetrisch zur

-Achse. Dies ist bei

der Fall.
 Schnittpunktkoordinaten bestimmen
Schnittpunktkoordinaten bestimmen
Du sollst die Koordinaten der Schnittpunkte des Graphen mit den Koordinatenachsen bestimmen. Um die Koordinaten der Schnittpunkte mit der

-Achse zu bestimmen, muss du den Funktionsterm gleich Null setzen. Die Koordinaten des Schnittpunkts mit der

-Achse kannst du berechnen, indem du Null in den Funktionsterm einsetzt.
Schnittpunkte mit der

-Achse:
Schnittpunkte mit der y-Achse:

Die Schnittpunkte mit der

-Achse liegen also bei

und

. Der Schnittpunkt mit der

-Achse liegt bei

.
 Koordinaten der Extrema berechnen
Koordinaten der Extrema berechnen
Jetzt sollen die Koordinaten der Extrem- und Wendepunkte des Graphen berechnnet werden. Dabei gibt es jeweils eine
notwendige Bedingung, die für die Existenz einer solchen Stelle erfüllt sein muss. Die Art der Stelle ergibt sich dann mit der
hinreichenden Bedingung (z.B. Hoch- oder Tiefpunkt).
Die notwendige Bedingung für eine Extremstelle ist

und die hinreichende Bedingung

.
Für eine Wendestelle lautet die notwendige Bedingung

und die hinreichende Bedingung

. Du musst also für diesen Aufgabenteil den Funktionsterm drei mal ableiten.
![\(\begin{array}[t]{rll}
f(x)&=& x^{4}-8x^{2}+7 &\quad \scriptsize \\[5pt]
f‘(x)&=& 4x^{3}-16x &\quad \scriptsize \\[5pt]
f‘‘(x)&=& 12x^{2}-16 &\quad \scriptsize \\[5pt]
f‘‘‘(x)&=& 24x &\quad \scriptsize\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b8e7cc5e81bcd77e3866c011f02f5d829a4e657287d7a4361c2b52bc84a572ba?color=5a5a5a)
Fordere nun

. Damit überprüfst du die notwendige Bedingung für eine Extremstelle von

.
Setze die erhaltenen

in die zweite Ableitung ein:
Setzt du die erhaltenen

in den Funktionsterm

ein, bekommst du die Koordinaten der Extrempunkte mit

,

und

.
 Koordinaten der Wendepunkte berechnen
Koordinaten der Wendepunkte berechnen
Das Vorgehen und die Bedingungen bei den Wendepunkten sind analog zu den Extrempunkten, nur dass alles eine Ableitungsebene höher stattfindet.
Überprüfe also zunächst die notwendige Bedingung mit

und weise die Wendestelle mit der hinreichenden Bedingung

nach.
![\(\begin{array}[t]{rll}
0 &=& 12x^{2}-16 &\quad \scriptsize \\[5pt]
x^{2} &=& \dfrac{4}{3} &\quad \scriptsize \\[5pt]
x_{1,2} &=& \pm\sqrt{\dfrac{4}{3}} &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/74944baa43832b0253c0225bd62f54aa42396545f2e03977a91758a6b23e3dce?color=5a5a5a)
Hinreichende Bedingung:
Die Wendepunkte haben die Koordinaten

und

.
1.2

 skizzieren
skizzieren
Überlege dir, welche Punkte auf dem Graphen du schon bestimmt hast, um ihn zu skizzieren. Verbinde dann diese Punkte und achte darauf, dass es sich um ein Polynom vierten Grades handelt.
1.3
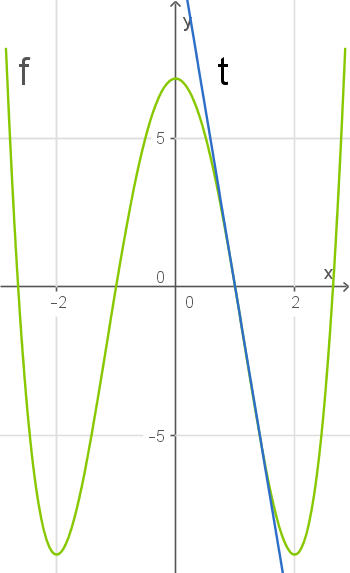
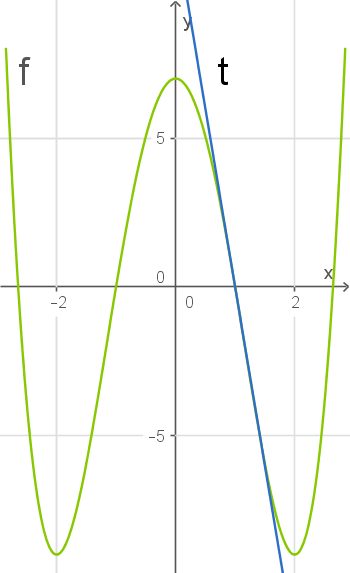
 Tangentengleichung bestimmen
Tangentengleichung bestimmen
Die Gleichung einer Tangente hat die Form

.

gibt dabei die Steigung und

den

-Achsen-Abschnitt an.
Da die erste Ableitung die Steigung des Graphen von

beschreibt, kannst du damit die Steigung an der Stelle

bestimmen. Dann kannst du die Steigung und einen bekannten Punkt auf der Tangente einsetzen, um

zu bestimmen.

Jetzt kannst du

und den die Koordinaten des Punkts

in die Tangentengleichung einsetzen und nach

auflösen.
![\(\begin{array}[t]{rll}
0 &=& -12\cdot1 + c &\quad \scriptsize \\[5pt]
c &=& 12
\end{array}\)](https://mathjax.schullv.de/99983a43ee465e4dd51e27a816367dd6475fddebb29fbe20179877ce716bf31f?color=5a5a5a)
Also ist

.
Die Tangente kannst du zeichnen, indem du zwei Punkte auf der Tangente bestimmst und durch diese eine Gerade zeichnest. Zum Beispiel erhältst du mit

und

die Punkte

und

.
 Stellen mit gleicher Steigung bestimmen
Stellen mit gleicher Steigung bestimmen
Es ist nach weiteren Stellen von

gefragt, an denen die Tangente die gleiche Steigung wie am Punkt

hat. Da die erste Ableitung die Steigung des Graphen angibt, muss also die Ableitung den Wert der Steigung annehmen. Die Steigung am Punkt

ist, wie gerade bestimmt,

.
Setze die erste Ableitung gleich

und löse nach

. Dabei musst du eine Polynomdivision durchführen.
![\(\begin{array}[t]{rll}
-12 &=& 4x^{3}-16x &\quad \scriptsize \\[5pt]
0 &=& 4x^{3}-16x+12 &\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6dd471c922be7849bf79bdbd37335725756a74bb6c60da7e9087fdbf1c73e22f?color=5a5a5a)
Da aus dem ersten Aufgabenteil schon

folgt, sieht die Division folgendermaßen aus:
Die so entstandene quadratische Gleichung kannst du zum Beispiel mit der

-Formel lösen.




An den Stellen

und

hat der Graph von

also die selbe Steigung wie bei

.
1.4
 Gleichung für
Gleichung für  bestimmen
bestimmen
Du hast in der Aufgabenstellung den Hinweis gegeben, dass die Gleichung für

eine quadratische Funktion sein muss. Diese hat die Form

. Nun kannst du die drei gegebenen Punkte einsetzen und so die Koeffizienten bestimmen.
1. Schritt:  einsetzen
einsetzen

 2. Schritt:
2. Schritt:  einsetzen
einsetzen

 3. Schritt:
3. Schritt:  einsetzen
einsetzen


Eine Gleichung für

ist also

.
1.5
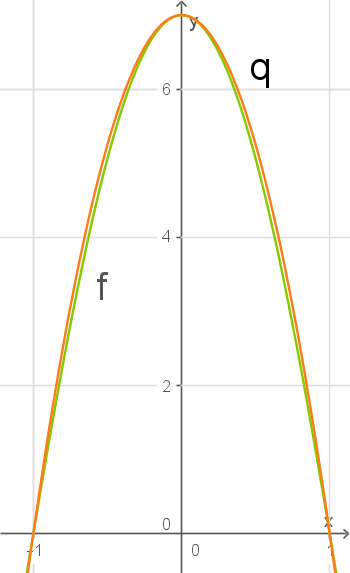
 Graph von
Graph von  skizzieren
skizzieren
Du sollst den Graph von

skizzieren. Da es sich um eine quadratische Funktion handelt, muss der Graph eine Parabel beschreiben. Wenn du zum Beispiel

und

einsetzt, kannst du drei Punkte auf dem Graph berechnen und diese dann parabelförmig verbinden.
 Maximale Differenz bestimmen
Maximale Differenz bestimmen
Die Differenz der beiden Funktionen

und

berschreibt wieder eine Funktion

. Das heißt, du kannst

nach Maximalstellen untersuchen, um die maximale Differenz zu berechnen. Der Funktionsterm ist, wie angegeben,

.
Um Maxima zu finden, setze die Ableitung von

gleich Null.
![\(\begin{array}[t]{rll}
d‘(x)&=&-4x^{3}+2x &\stackrel{!}{=} 0 \\[5pt]
x_{1}&=& 0 &x_{2,3}=\pm\sqrt{\dfrac{1}{2}}
\end{array}\)](https://mathjax.schullv.de/fe797a8cdfbffcb1f2b3e2d258e90052612bb082e49c62e2ac1482dc358efc4a?color=5a5a5a)
An der Stelle

ist

Null. Damit kann die Differenz dort nicht maximal sein. Setze also noch

in

ein.
![\(\begin{array}[t]{rll}
d\left(\pm\frac{1}{2}\right)&=& -\left(\pm\sqrt{\frac{1}{2}}\right)^{4}+\left(\pm\sqrt{\frac{1}{2}}\right)^{2} &\quad \scriptsize \\[5pt]
&=&\dfrac{1}{4}
\end{array}\)](https://mathjax.schullv.de/16b0042aad51a452c149e0bac08628e4ffc17755a8e7e50d33e40654513f01ab?color=5a5a5a)
Somit ist die maximale Differenz von

und

im Intervall

ist

bei

.
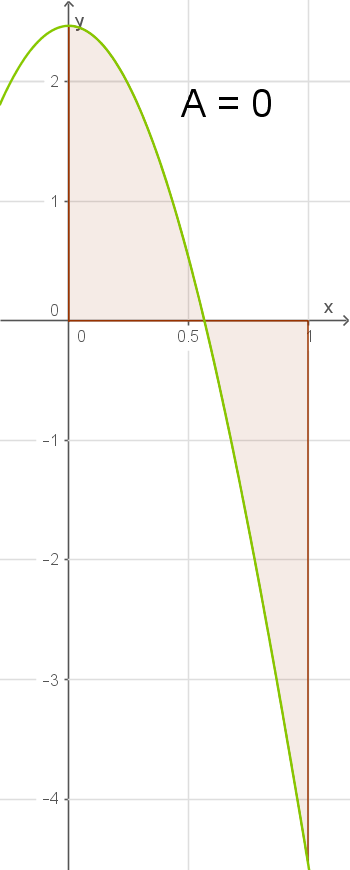
1.6
 Wert von
Wert von  bestimmen
bestimmen
Die Funktionenschar

hat für jedes

einen anderen Graphen. Du sollst nun das

bestimmen, für das dieser Graph im Intervall von

bis

zwei gleich große Teilflächen über- und unterhalb der

-Achse mit der

-Achse einschließt. Den Flächeninhalt zwischen einem Graph und der

-Achse berechnest du mit dem Integral. Da ein Teil des Integrals unter der

-Achse liegt und der andere darüber, heben sich beide Flächeninhalte in einer Integralfunktion von

bis

auf und der gesamte Flächeninhalt muss

sein.
Es gilt also:


$\begin{array}[t]{rll} \displaystyle\int_{0}^{1}f_{a}(x)\;\mathrm dx &=& 0&\quad \scriptsize \\[5pt] \left[F_{a}(x)\right]_{0}^{1}&=& 0&\quad \scriptsize \mid\;\text{Stammfunktion bilden}\\[5pt] \left[\frac{1}{5}x^{5}-\frac{8}{3}x^{3}+ax\right]_{0}^{1}&=& 0&\quad \scriptsize \mid\;\text{Grenzen einsetzen}\\[5pt] \frac{1}{5}1^{5}-\frac{8}{3}1^{3}+a\cdot1&=& 0 &\quad \scriptsize \mid\;\text{Zusammenfassen und nach

auflösen} \\[5pt] a&=&\dfrac{37}{15} \end{array}$
Die beiden Teilflächen sind gleich groß, wenn für die Schar

gilt.
Bildnachweise [nach oben]
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
 mit der Gleichung
mit der Gleichung  mit
mit  .
.
 ist
ist  .
.
 . Begründe.
Ermittle die Koordinaten der Schnittpunkte von
. Begründe.
Ermittle die Koordinaten der Schnittpunkte von  mit den Koordinatenachsen.
mit den Koordinatenachsen.
 .
.
 im Intervall
im Intervall  in einem geeigneten Koordinatensystem.
in einem geeigneten Koordinatensystem.
 an
an  im Punkt
im Punkt  .
Zeichne
.
Zeichne  in das Koordinatensystem.
in das Koordinatensystem.
 parallel zu
parallel zu  verläuft. Gib diese Stellen näherungsweise an.
verläuft. Gib diese Stellen näherungsweise an.
 verläuft durch die Punkte
verläuft durch die Punkte  ,
,  und
und  .
Bestimme eine Gleichung für
.
Bestimme eine Gleichung für  .
.
 wird die Funktion
wird die Funktion  mit
mit  mit
mit  als Näherungsfunktion für
als Näherungsfunktion für  verwendet.
verwendet.
 im Koordinatensystem aus Aufgabe 1.2.
im Koordinatensystem aus Aufgabe 1.2.
 , an denen die Differenz
, an denen die Differenz  maximal wird.
Gib die maximale Differenz an.
maximal wird.
Gib die maximale Differenz an.
 mit der Gleichung
mit der Gleichung
 mit
mit  .
Für jeden Wert von
.
Für jeden Wert von  begrenzen der Graph von
begrenzen der Graph von  , die
, die  Achse und die Geraden
Achse und die Geraden  und
und  zwei Teilflächen.
zwei Teilflächen.
 so, dass die Inhalte der beiden Teilflächen übereinstimmen.
so, dass die Inhalte der beiden Teilflächen übereinstimmen.