Analytische Geometrie
3
In einem kartesischen Koordinatensystem sind die Eckpunkte 





 und
und  gegeben.
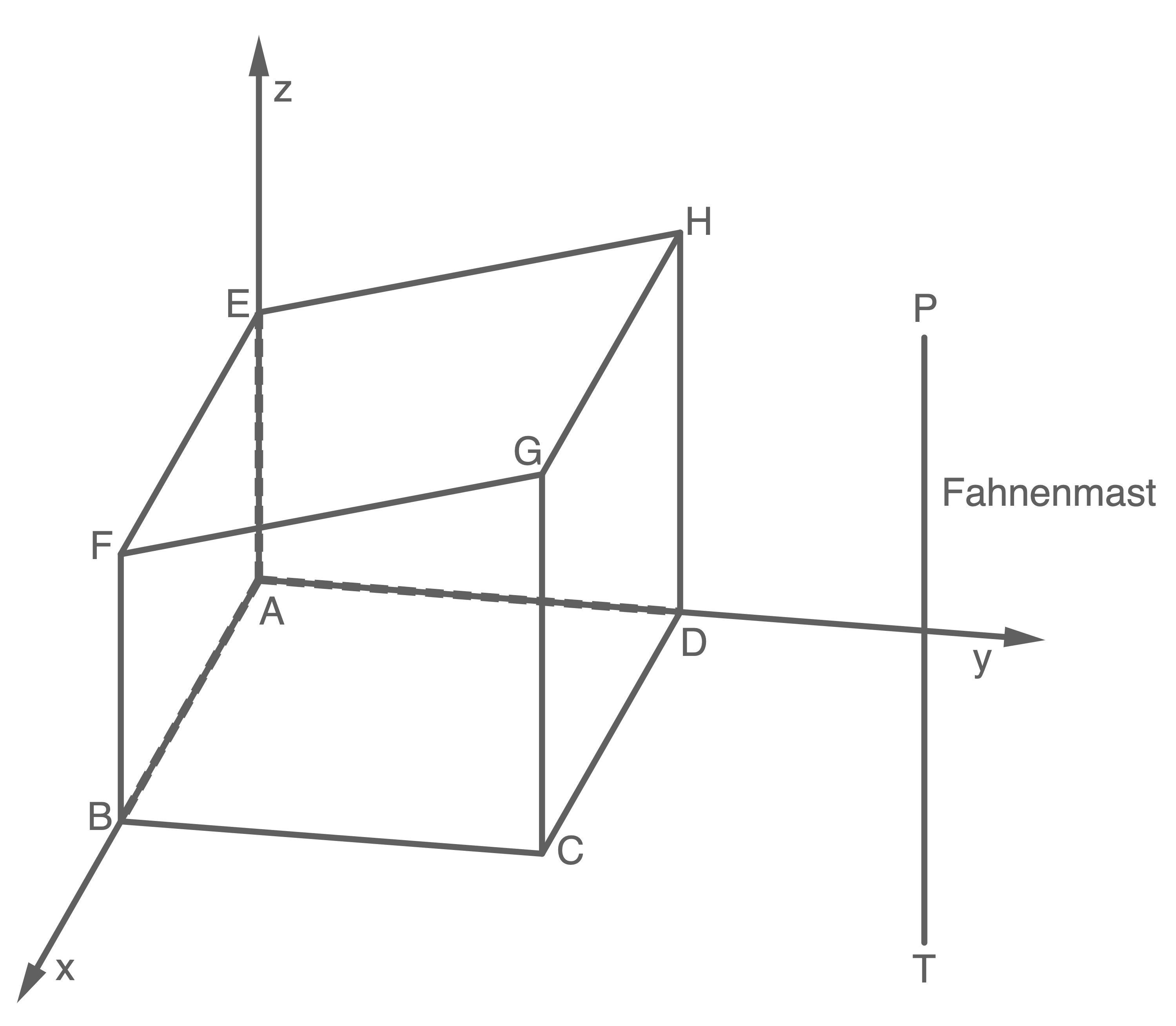
Betrachtet wird das Modell eines Gewächshauses
gegeben.
Betrachtet wird das Modell eines Gewächshauses  dabei stellen
dabei stellen  die Dachfläche und
die Dachfläche und  die Bodenfläche dar. Im verwendeten Koordinatensystem beschreibt die
die Bodenfläche dar. Im verwendeten Koordinatensystem beschreibt die  -Ebene den horizontalen Untergrund. Eine Längeneinheit entspricht einem Meter.
-Ebene den horizontalen Untergrund. Eine Längeneinheit entspricht einem Meter.
3.1
Begründe, dass die Fläche  ein Rechteck ist.
ein Rechteck ist.
(3 BE)
3.2
Neben dem Gewächshaus steht senkrecht ein  hoher Mast. Sein Fußpunkt wird im Modell mit dem Punkt
hoher Mast. Sein Fußpunkt wird im Modell mit dem Punkt  beschrieben. Die Dicke des Mastes wird vernachlässigt.
beschrieben. Die Dicke des Mastes wird vernachlässigt.
3.2.1
Sonnenlicht fällt mit der Richtung  auf den Mast. Der Punkt
auf den Mast. Der Punkt  ist der Schattenpunkt der Mastspitze
ist der Schattenpunkt der Mastspitze  auf dem Boden.
auf dem Boden.
Zeige, dass die Koordinaten
die Koordinaten  hat.
hat.
Beurteile, ob der Schattenpunkt auf der Kante
auf der Kante  liegt.
liegt.
Zeige, dass
Beurteile, ob der Schattenpunkt
(5 BE)
3.2.2
Der Mast knickt durch einen Sturm in einer Höhe von  Metern über dem Erdboden ab. Dabei reißt er nicht vollständig ab, sodass nur die Spitze auf dem Boden aufliegt. Der abgeknickte Teil schließt mit dem noch stehenden Teil des Mastes einen Winkel von 60° ein.
Metern über dem Erdboden ab. Dabei reißt er nicht vollständig ab, sodass nur die Spitze auf dem Boden aufliegt. Der abgeknickte Teil schließt mit dem noch stehenden Teil des Mastes einen Winkel von 60° ein.
Ermittle den Wert von
Ermittle den Wert von
(2 BE)
4
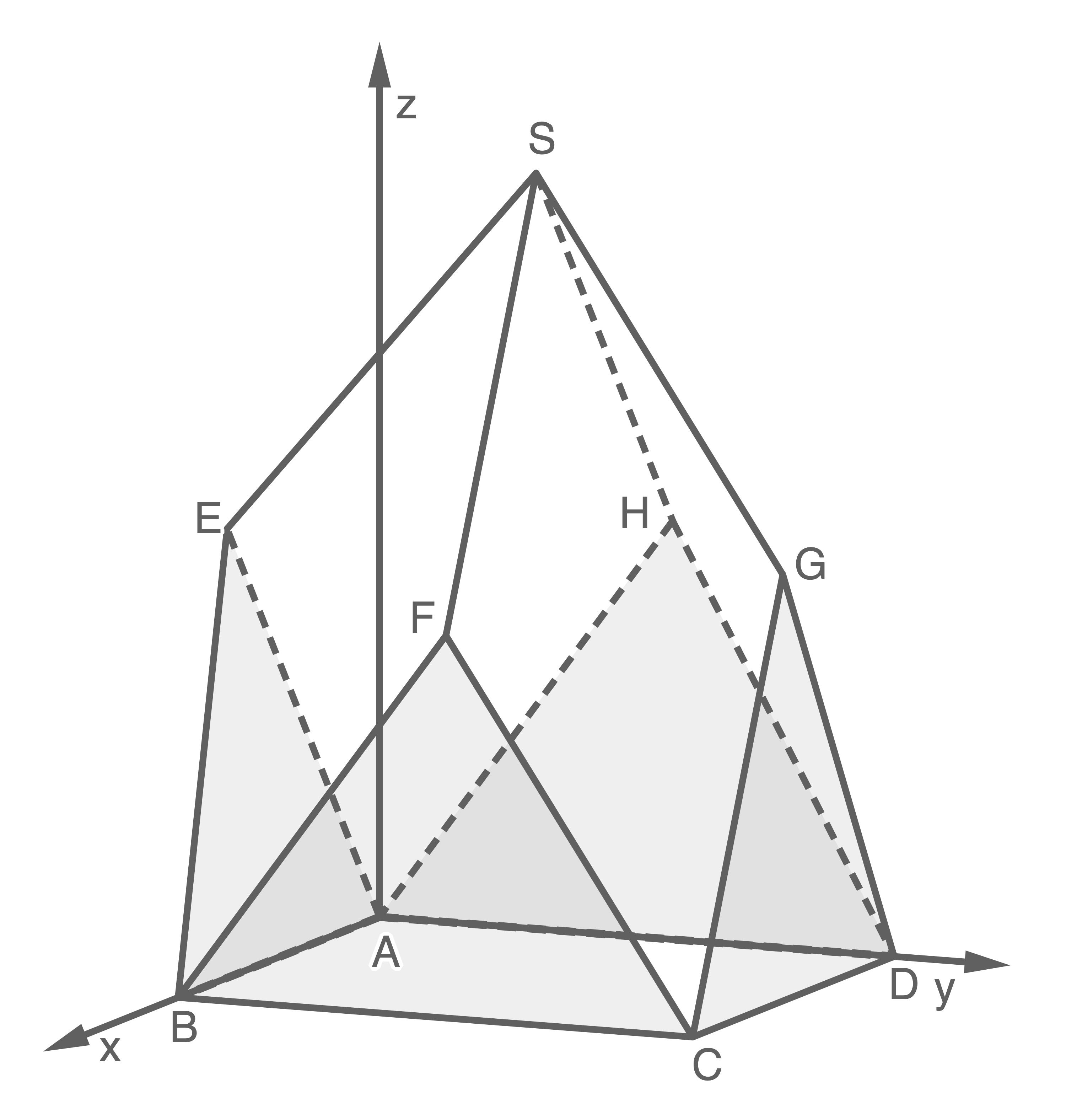
Die Abbildung zeigt modellhaft das Dach eines Kirchturms. Die Eckpunkte der dreieckigen Giebelflächen (grau markiert) und der viereckigen Dachflächen werden durch die Punkte 






 und
und  dargestellt. Die vier Dachflächen haben die gleiche Form und die gleiche Größe. Im verwendeten Koordinatensystem entspricht eine Längeneinheit einem Meter in der Realität. Die Materialstärken der Bauteile des Dachs sollen im Folgenden vernachlässigt werden.
dargestellt. Die vier Dachflächen haben die gleiche Form und die gleiche Größe. Im verwendeten Koordinatensystem entspricht eine Längeneinheit einem Meter in der Realität. Die Materialstärken der Bauteile des Dachs sollen im Folgenden vernachlässigt werden.
4.1
Die Ebene  enthält die Punkte
enthält die Punkte 
 und
und  Gib eine Gleichung von
Gib eine Gleichung von  in Parameterform an und zeige, dass auch
in Parameterform an und zeige, dass auch  in
in  liegt.
liegt.
(3 BE)
4.2
Weise nach, dass das Viereck  eine Raute ist.
eine Raute ist.
(2 BE)
4.3
Gegeben sind drei Ebenen mit den folgenden Gleichungen:


 Eine dieser Ebenen stellt eine Symmetrieebene des Kirchendachs dar. Gib diese Ebene an und beschreibe ihre Lage.
Eine dieser Ebenen stellt eine Symmetrieebene des Kirchendachs dar. Gib diese Ebene an und beschreibe ihre Lage.
(2 BE)
4.4
Berechne die Größe des Innenwinkels des Vierecks  im Punkt
im Punkt  sowie den gesamten Flächeninhalt der Dachflächen.
sowie den gesamten Flächeninhalt der Dachflächen.
(6 BE)
4.5
Die Gerade  verläuft durch
verläuft durch  und
und  die Gerade
die Gerade  durch
durch  und
und  Die beiden Geraden schneiden die
Die beiden Geraden schneiden die  -Ebene in den Punkten
-Ebene in den Punkten  bzw.
bzw. 
Gib das Verhältnis des Abstands von und
und  zum Abstand von
zum Abstand von  und
und  an.
an.
Begründe deine Angabe, ohne die Koordinaten von und
und  zu berechnen.
zu berechnen.
Gib das Verhältnis des Abstands von
Begründe deine Angabe, ohne die Koordinaten von
(3 BE)
4.6
Zur Stabilisierung wird zwischen den durch  und
und  dargestellten Giebelspitzen ein gerader Stahlträger montiert. Vom Mittelpunkt dieses Stahlträgers aus soll eine möglichst kurze Stütze zum durch
dargestellten Giebelspitzen ein gerader Stahlträger montiert. Vom Mittelpunkt dieses Stahlträgers aus soll eine möglichst kurze Stütze zum durch  dargestellten Balken verlaufen. Der Punkt, in dem die Stütze auf den Balken trifft, wird im Modell mit
dargestellten Balken verlaufen. Der Punkt, in dem die Stütze auf den Balken trifft, wird im Modell mit  bezeichnet;
bezeichnet;  stimmt weder mit
stimmt weder mit  noch mit
noch mit  überein.
überein.
Beschreibe, wie man die Koordinaten von ermitteln könnte.
ermitteln könnte.
Beschreibe, wie man die Koordinaten von
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
Aus  und
und  folgt, die Seiten des Vierecks sind paarweise parallel und gleichlang.
Aus
folgt, die Seiten des Vierecks sind paarweise parallel und gleichlang.
Aus  folgt, dass es ein Rechteck ist.
folgt, dass es ein Rechteck ist.
3.2.1
Koordinaten zeigen
Gerade, die das Sonnenlicht beschreibt:

 Aus
Aus  folgt:
folgt: 
 in
in  eingesetzt ergibt
eingesetzt ergibt 
 in
in  eingesetzt ergibt
eingesetzt ergibt  Damit ist gezeigt, dass
Damit ist gezeigt, dass  die Koordinaten
die Koordinaten  hat.
Beurteilen
hat.
Beurteilen
 liegt aus der Kante
liegt aus der Kante  weil die
weil die  - und
- und  -Koordinate von
-Koordinate von  und
und  jeweils gleich sind und für die
jeweils gleich sind und für die  -Koordinate von
-Koordinate von  gilt:
gilt: 
3.2.2.
4.1
4.2
4.3
4.4
4.5
Die Dreiecke  und
und  haben bei
haben bei  einen gemeinsamen Innenwinkel, die Gerade
einen gemeinsamen Innenwinkel, die Gerade  ist parallel zur Gerade
ist parallel zur Gerade  Damit sind die beiden Dreiecke ähnlich.
Damit sind die beiden Dreiecke ähnlich.
 ist doppelt so lang wie
ist doppelt so lang wie  Folglich ist der Abstand von
Folglich ist der Abstand von  und
und  doppelt so groß wie der Abstand von
doppelt so groß wie der Abstand von  und
und 
4.6
Es wird der Mittelpunkt  von
von  bestimmt.
Mit
bestimmt.
Mit  liefert
liefert  den Wert von
den Wert von  und damit die Koordinaten von
und damit die Koordinaten von 