Wahlteil A1

A1 Analysis

Gegeben ist eine Funktion $f$ mit der Gleichung

$\begin{array}{lrll} f(x) &=& (x+1)^2 \cdot (2x-3)&\quad \\ &=& 2x^3+x^2-4x-3 \\ \end{array}$

mit $x \in \mathbb{R}.$

Der Graph von $f$ ist $K.$

1.1

Ermittle die Nullstellen von $f.$
Gib die Koordinaten des Schnittpunktes $A$ mit der $y$ -Achse an.
Berechne die Koordinaten der Extrem- und Wendepunkte von $K$ .
Weise die Art der Extrema und die Existenz des Wendepunktes nach.
Begründe, dass für $K$ beim Wendepunkt ein Wechsel von rechtsgekrümmt nach linksgekrümmt erfolgt.

Gib die benötigten Ableitungsfunktionen an.

(11 BE)

1.2

Skizziere $K$ in ein geeignetes Koordinatensystem.

(2 BE)

1.3

$K$ schneidet die $y$ -Achse im Punkt $A$ und den positiven Teil der $x$ -Achse im Punkt $B.$
$K$ und die Strecke $\overline{AB}$ schließen eine Fläche vollständig ein.

Schraffiere diese Fläche im Koordinatensystem von Aufgabe 1.2.

Berechne den Inhalt dieser Fläche.
Gib die verwendete Stammfunktion an.

(5 BE)

1.4

Ermittle eine Gleichung der Tangente $t_1$ an $K$ an der Stelle $x=\dfrac{3}{2}.$
Berechne die Größe des Winkels, den $t_1$ mit der $x$ -Achse einschließt.

Eine weitere zu $t_1$ parallele Tangente $t_2$ berührt $K.$
Bestimme die Koordinaten des Berührungspunktes von $t_2$ an $K.$

(7 BE)

1.5

Gegeben ist die Funktion $g$ mit der Gleichung $g(x)=-x^2+\dfrac{1}{2}x+\dfrac{3}{2}.$

Berechne die Stelle $x$ mit $-\dfrac{5}{2}\leq x\leq\dfrac{3}{2}$ , an der die Differenz $g(x) - f(x)$ am größten wird.
Gib die maximale Differenz an.

(6 BE)

1.6

Für jeden Wert von $s$ mit $s\neq 0$ ist eine Funktion $h_s$ gegeben durch $h_s(x)=s \cdot (x+1)^2$ mit $x \in \mathbb{R}.$ Der Graph von $h_s$ sei $H_s.$

1.6.1

Zeichne den Graphen $H_s$ für $s=2$ in die grafische Darstellung aus 1.2 ein.

(1 BE)

1.6.2

Begründe, dass es einen Punkt $R$ gibt, in dem alle Graphen $H_s$ die Kurve $K$ berühren und dessen Koordinaten unabhängig von $s$ sind.

Gib die Koordinaten des Punktes $R$ an.

(3 BE)

1.1

$f(x)=(x+1)^2 \cdot (2x-3)$ $=2x^3+x^2-4x-3$

Nullstellen von $f$ : Setze $f(x)=0$

$(x+1)^2 \cdot (2x-3)=0$

$\begin{array}[t]{rll} 0&=&(x+1)^2 &\quad \scriptsize \mid\;\sqrt{\,} \\[5pt] 0&=&x+1 &\quad \scriptsize \mid\;-1 \\[5pt] -1&=&x \end{array}$

$\begin{array}[t]{rll} 0&=&(2x-3) &\quad \scriptsize \mid\;+3 \\[5pt] 3&=&2x &\quad \scriptsize \mid\;:2 \\[5pt] \dfrac{3}{2}&=&x \end{array}$

Nullstellen von $f$ sind $x_1=-1$ und $x_2=\dfrac{3}{2}$ .

Schnittpunkt mit der $y-$ Achse:

$f(0)=2 \cdot 0^3+0^2-4 \cdot 0-3=-3$

$A(0\mid-3)$

Ableitungen:

$\(\begin{array}[t]{rll} f$

Notwendiges Kriterium für Extrema: $\(f$

$\begin{array}[t]{rll} 0&=& 6x^2+2x-4&\quad \scriptsize \mid\;:6 \\[5pt] 0&=&x^2+\dfrac{1}{3}x-\dfrac{2}{3} &\quad \scriptsize \mid\;pq-\text{Formel} \\[5pt] x_{3,4}&=& -\dfrac{\frac{1}{3}}{2} \pm \sqrt{\left(\dfrac{\frac{1}{3}}{2}\right)^2+\dfrac{2}{3}} \\[5pt] &=&-\dfrac{1}{6}\pm\dfrac{5}{6} &\quad \\[5pt] \end{array}$

$x_3=x_1=-1\;,\quad x_4=\dfrac{2}{3}$

Hinreichendes Kriterium für Extrema: $\(f$

$\(f$

$f(-1)=0$

Der lokale Hochpunkt hat die Koordinaten $(-1\mid0)$ .

$\(f$

$f\left(\frac{2}{3}\right)=2\left(\frac{2}{3}\right)^3+\left(\frac{2}{3}\right)^2-4\left(\frac{2}{3}\right)-3=-\frac{125}{27}$

Der lokale Tiefpunkt hat die Koordinaten $\left(\dfrac{2}{3}\mid-\dfrac{125}{27}\right)$ .

Wendepunkte:
Notwendiges Kriterium für Wendestellen: $\(f$

$\begin{array}[t]{rll} 12x+2&=&0 &\quad \scriptsize \mid\;-2\mid\;:12 \\[5pt] x_w&=&-\dfrac{1}{6} \end{array}$

Hinreichendes Kriterium für Wendestellen: $\(f$

$\(f$

Der Wendepunkt hat die Koordinaten $\left(-\dfrac{1}{6}\mid-\dfrac{125}{54}\right)$ .

Nachweis Krümmungswechsel:

Da $\(f$ gilt, ist der Graph von rechts- nach linksgekrümmt.

Alternativ:

Für $x\lt-\dfrac{1}{6}$ ist $\(f$ und somit eine Rechtskurve.

Für $x\gt-\dfrac{1}{6}$ ist $\(f$ und somit eine Linkskurve.

Da der Graph zuerst eine Rechtskurve und dann eine Linkskurve hat, wechselt er von einer Rechtskrümmung zu einer Linkskrümmung.

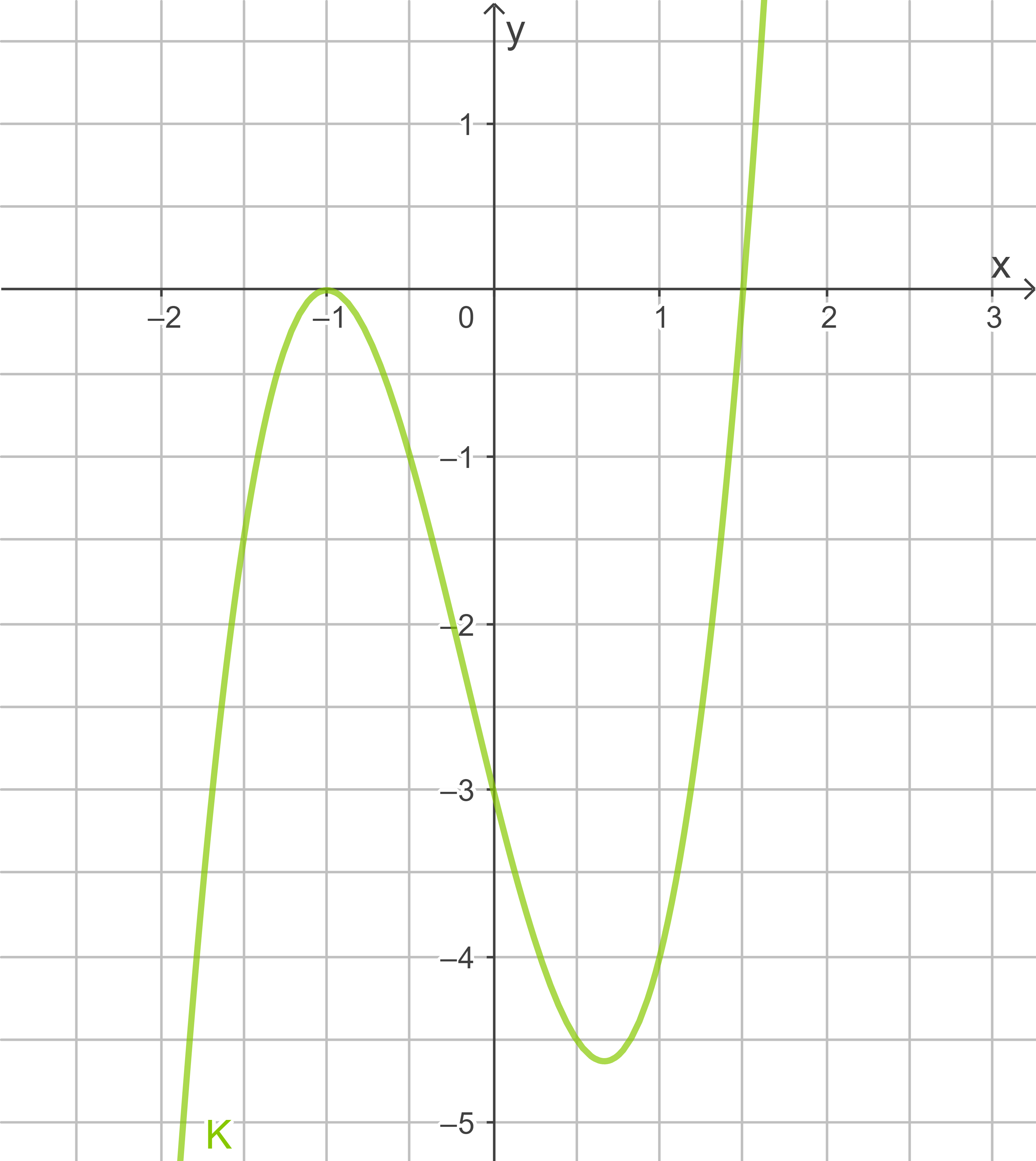
1.2

Skizze $K$ im Koordinatensystem:

Graph einer Funktion im Koordinatensystem mit einer grünen Kurve und Gitterlinien.

1.3

Kennzeichnung der Fläche:

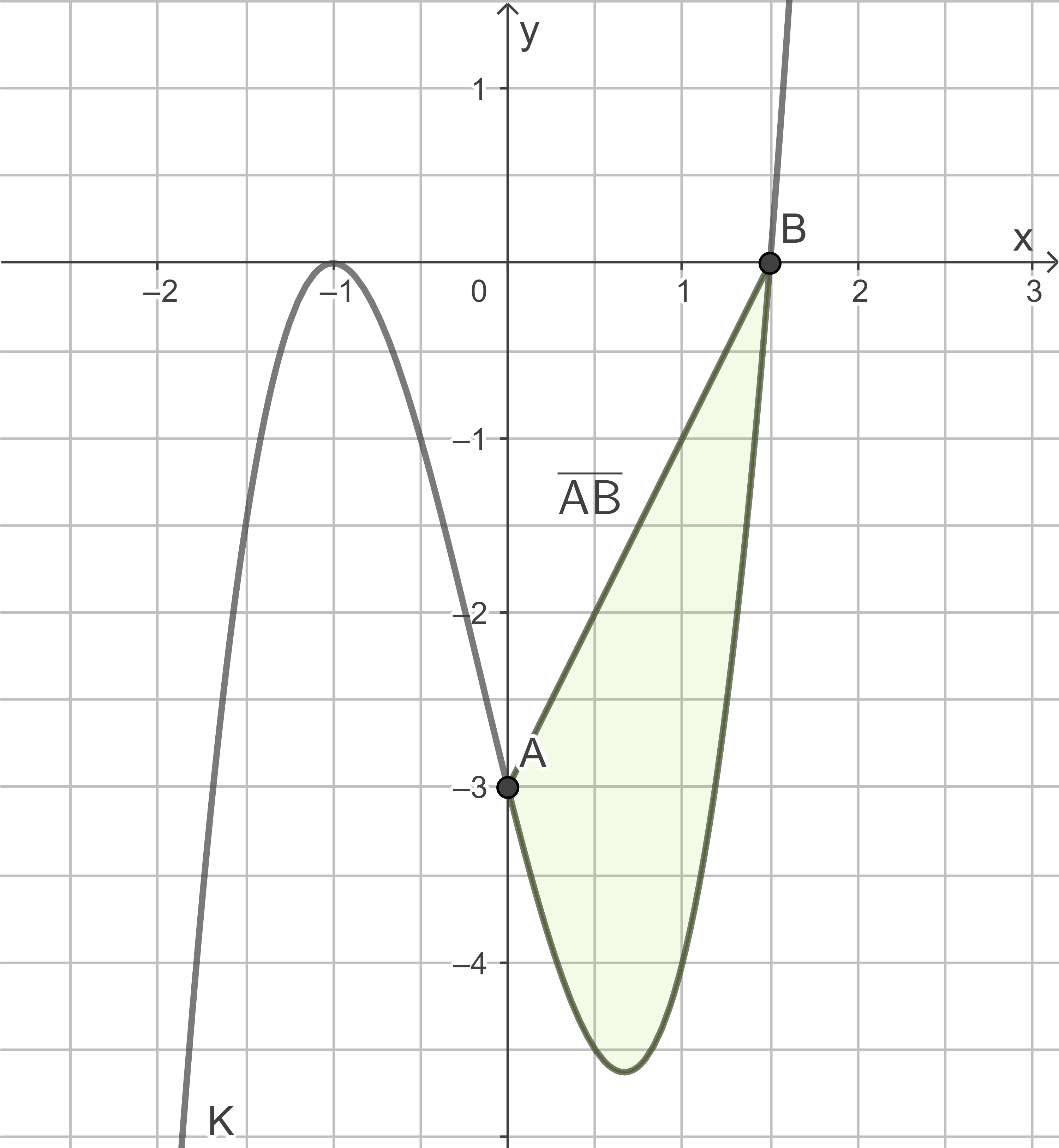
Grafik einer Funktion mit den Punkten A und B sowie einem schattierten Bereich zwischen den Punkten.

Berechnung Flächeninhalt:

Gleichung der Geraden $p$ durch $A(0\mid-3)$ und $B\left(\frac{3}{2}\mid0\right)$ aufstellen:

$f(x)=m \cdot x+n$

$m=\dfrac{y_2-y_1}{x_2-x_1}$ $=\dfrac{0-(-3)}{\frac{3}{2}-0}=2$

Wegen $A(0\mid-3)$ ist der $y-$ Achsenabschnitt $n=-3$ .

$p(A,B): p(x)=2x-3$

Fläche zwischen den Graphen $p$ und $f$ bestimmen:

$\begin{array}[t]{rll} A&=&\displaystyle\int_{0}^{\frac{3}{2}}p(x)-f(x) \;\mathrm {dx} \\[5pt] &=&\displaystyle\int_{0}^{\frac{3}{2}}(2x-3)-(2x^3+x^2-4x-3)\; \mathrm {dx} \\[5pt] &=&\displaystyle\int_{0}^{\frac{3}{2}}-2x^3-x^2+6x \;\mathrm {dx} \\[5pt] &=&\left[-\dfrac{1}{2}x^4-\dfrac{1}{3}x^3+3x^2 \right]_0 ^\frac{3}{2} \\[5pt] &=&\left(-\dfrac{81}{32}-\dfrac{9}{8}+\dfrac{27}{4}\right)-0 \\[5pt] &=&\dfrac{99}{32}\approx3,09 \end{array}$

Alternativ:

$\begin{array}[t]{rll} A&=&A_{f[0;1,5]}-A_{\text{Dreieck}:OAB} \\[5pt] &=&\,\bigg \vert \,\displaystyle\int_{0}^{1,5}f(x)\;\mathrm {dx} \,\bigg \vert -\dfrac{1}{2} \cdot 3 \cdot \dfrac{3}{2} \\[5pt] &=&\,\bigg \vert \,\bigg[\dfrac{1}{2}x^4+\dfrac{1}{3}x^3-2x^2-3x \bigg]_0 ^{1,5}\,\bigg \vert \, - \dfrac{9}{4} \\[5pt] &=&\,\bigg \vert \,\left(\dfrac{81}{32}+\dfrac{9}{8}-\dfrac{9}{2}-\dfrac{9}{2}\right)-0\,\bigg \vert \,-\dfrac{9}{4} \\[5pt] &=&\dfrac{99}{32} \end{array}$

1.4

Tangentengleichung:

$t_1(x)=m_{t_1} \cdot x+n_{t_1}$

$\(m_{t_1}=f$ $=6 \cdot \left(\dfrac{3}{2}\right)^2+2 \cdot\dfrac{3}{2}-4=\dfrac{25}{2}$

Berührpunkt: $f\left(\dfrac{3}{2}\right)=0$

Einsetzen in $t_1(x)$ :

$\begin{array}[t]{rll} \dfrac{25}{2} \cdot \dfrac{3}{2}+n_{t_1}&=&0 &\quad \scriptsize \mid\;-\frac{75}{4} \\[5pt] n_{t_1}&=&-\dfrac{75}{4} \end{array}$

$t_1(x)=\dfrac{25}{2}x-\dfrac{75}{4}$

Schnittwinkel mit der $x-$ Achse:

$\begin{array}[t]{rll} \tan(\alpha)&=& m_{t_1}&\quad\\[5pt] \tan(\alpha)&=& \dfrac{25}{2}&\quad \scriptsize \mid\;\tan^{-1} \\[5pt] \alpha&\approx&85,4^{\circ} \end{array}$

Berührpunkt:

Da die Tangente $t_2$ parallel zu $t_1$ ist, besitzen sie die gleiche Steigung.

$t_2:t_2(x)=\dfrac{25}{2}x+n_{t_2}$

Stelle mit dem Anstieg $\dfrac{25}{2}$ : $\(\quad f$

$\begin{array}[t]{rll} \dfrac{25}{2}&=&6x^2+2x-4 &\quad \scriptsize \mid\;-\dfrac{25}{2} \\[5pt] 0&=&6x^2+2x-\dfrac{33}{2} &\quad \scriptsize \mid\;:6 \\[5pt] 0&=&x^2+\dfrac{1}{3}x-\dfrac{11}{4} &\quad \scriptsize \mid\;pq-\text{Formel} \\[5pt] x_{1/2}&=&-\dfrac{1}{6}\pm \sqrt{\dfrac{1}{36}+\dfrac{11}{4}} \\[5pt] x_1&=&\dfrac{3}{2} \\[5pt] x_2&=&-\dfrac{11}{6} \end{array}$

Berührpunkt $t_2$ : $f\left(-\dfrac{11}{6}\right)=-\dfrac{125}{27}$

Der Berührpunkt hat die Koordinaten $\left(-\dfrac{11}{6}\,\bigg \vert \,-\dfrac{125}{27}\right)$ .

1.5

$f(x)=2x^3+x^2-4x-3$

$g(x)=-x^2+\dfrac{1}{2}x+\dfrac{3}{2}$

$d(x)=-2x^3-2x^2+\dfrac{9}{2}x+\dfrac{9}{2}$

Vollständige Lösung anzeigen

$\(\begin{array}[t]{rll} d$

Berechnung lokale Extrema:

Notwendiges Kriterium für Extremstellen : $\(d$

$\begin{array}[t]{rll} 0&=&-6x^2-4x+\dfrac{9}{2} &\quad \scriptsize \mid\;:(-6) \\[5pt] 0&=&x^2+\dfrac{2}{3}x-\dfrac{3}{4} &\quad \scriptsize \mid\;pq-\text{Formel} \\[5pt] x_{1/2}&=&-\dfrac{1}{3}\pm\sqrt{\dfrac{1}{9}+\dfrac{3}{4}} \\[5pt] x_1&=&-\dfrac{2+\sqrt{31}}{6}\approx-1,25 \\[5pt] x_2&=&\dfrac{-2+\sqrt{31}}{6}\approx0,59 \end{array}$

Hinreichendes Kriterium für Extremstellen:

$\(d$ lokales Minimum
$\(d$ lokales Maximum

$d(x_2)\approx6,05$

Der lokale Hochpunkt liegt bei $H(0,59\mid6,05).$

Berechnung globales Maximum:

$d\left(-\dfrac{5}{2}\right)=12$ und $d\left(\dfrac{3}{2}\right)=0$
Die globale Extremstelle liegt bei $x=-\frac{5}{2}$ , die Differenz zu $x=\frac{3}{2}$ ist mit $12$ die maximale Differenz.

1.6.1

Zeichnung des Graphen $H_2$ :

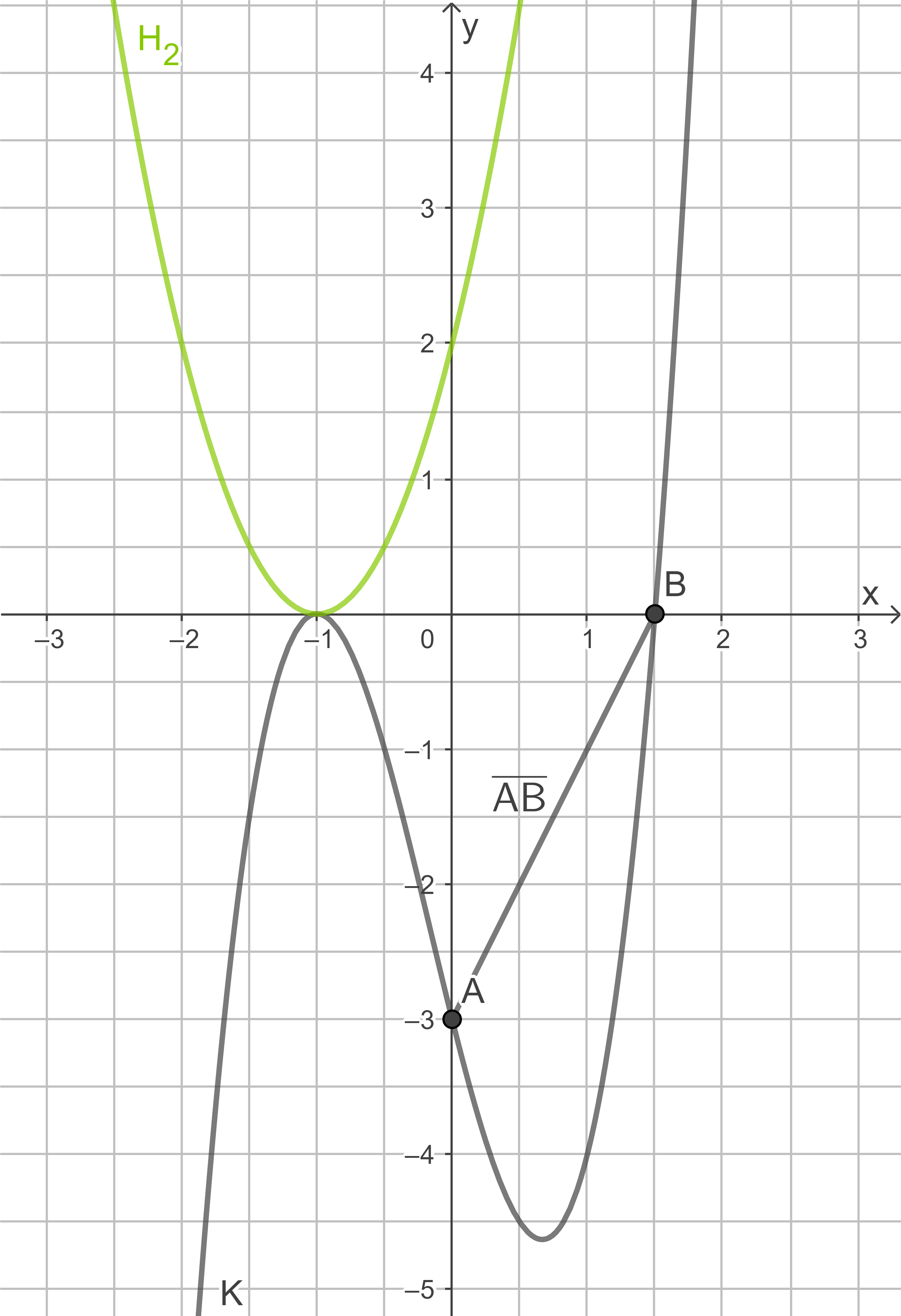
Grafik mit zwei Parabeln im Koordinatensystem, gekennzeichnete Punkte A und B.

1.6.2

Die Graphen $H_s$ berühren die Kurve $K$ , das bedeutet sie besitzen einen gemeinsamen Punkt mit dem gleichem Anstieg.

gemeinsamer Punkt:

Die Koordinaten der Scheitelpunkte aller Graphen der Schar sind unabhängig vom Parameter $s$ und stimmen mit den Koordinaten des Hochpunktes von $K$ überein: $R(-1\mid0)$ .

gleicher Anstieg:

Aus der Zeichnung kann man entnehmen, dass der Anstieg für $K$ und $H_s$ an der Stelle $x=-1$ null ist.

Außerdem haben $K$ und $H_s$ an der Stelle $x=-1$ eine Extremstelle, deshalb muss die Steigung bei $x=-1$ null sein.