4 Analytische Geometrie
Bei Erdarbeiten werden Schuttmulden als Auffang- und Transportbehälter genutzt. Die betrachtete Schuttmulde hat die Form eines geraden Prismas mit fünfeckiger Grundfläche.
Die Ecken der Schuttmulde werden in einem Koordinatensystem durch die Punkte 
und 
sowie 
und 
modelliert. Die Fläche 
stellt dabei den Boden der Schuttmulde dar. Die Mulde ist oben und links oben offen (vgl. Abbildungen 1 und 2).
Eine Längeneinheit im Koordinatensystem entspricht einem Dezimeter in der Realität.
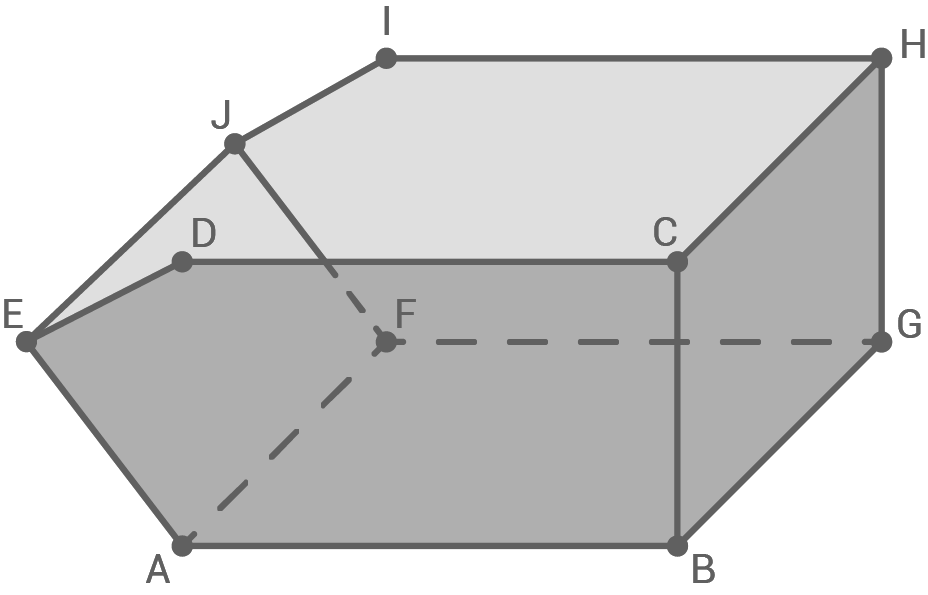
Abbildung 1: Schuttmulde
Abbildung 2: Schuttmulde im Modell
4.1
Begründe, dass die Fläche 
in der 
-Ebene liegt.
(2 BE)
4.2
Ermittle das Volumen des Prismas 
und gib das Fassungsvermögen der Schuttmulde in Kubikmetern an.
(4 BE)
4.3
In der Mulde befindet sich eine gerade, dünne Eisenstange. Das untere Ende der Stange liegt in einer Ecke der Mulde, im Modell ist dies der Punkt 
Das obere Ende lehnt in der Mitte einer gegenüberliegenden Kante an, im Modell im Mittelpunkt der Kante 
4.3.1
Berechne die Länge dieser Stange in Zentimeter sowie den Neigungswinkel der Stange gegenüber dem Boden der Mulde.
(6 BE)
4.3.2
In der Abbildung 1 ist ein Bagger zu sehen, der sich hinter der Schuttmulde befindet. Eine Fahrerin ist in den Bagger eingestiegen und blickt in die Mulde von einem Punkt aus, der im Modell die Koordinaten 
hat.
Zeige, dass ihr Blick auf das obere Ende der Stange nicht durch eine Seitenwand der Schuttmulde verdeckt wird.
(4 BE)
4.4
Eine solche Schuttmulde wird auf einen ebenen horizontalen Untergrund gestellt und als Auffangbehälter für Regenwasser genutzt. Aufgrund der oben offenen Bauweise kann die Schuttmulde nicht vollständig mit Wasser befüllt werden. Durch Ankippen der Mulde wird das Auffangvolumen maximiert (siehe Abbildung 3).
Erläutere, wie die Größe des zugehörigen Neigungswinkels der Bodenfläche gegenüber dem Untergrund berechnet werden kann.
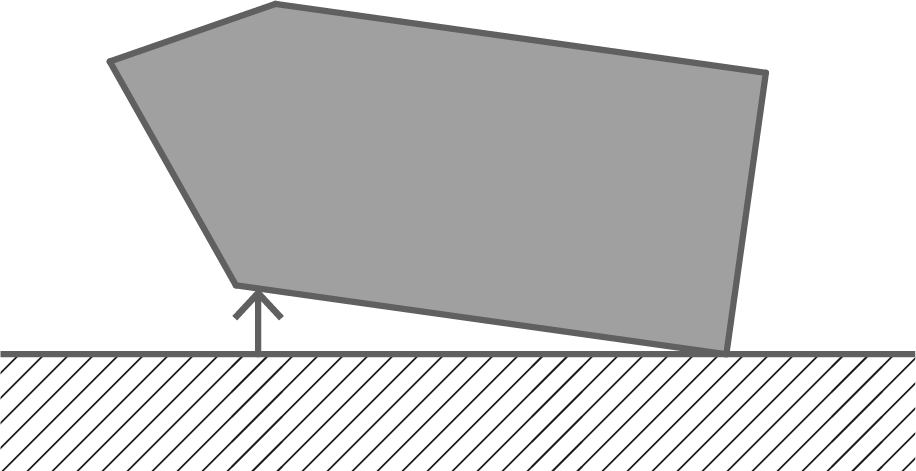
Abbildung 3: Seitenansicht des Modells der Mulde im angekippten Zustand
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
4.1
Alle Eckpunkte der Fläche 
liegen in der Ebene 
Da das Modell ein Prisma ist und der Punkt 
die 
- Koordinate 
besitzt, liegen alle Punkte der Fläche in der -Ebene.
4.2
1. Schritt: Flächeninhalt der Grundfläche berechnen
Die Grundfläche des Prismas kann in das Rechteck 
und das Dreieck 
aufgeteilt werden.
Die benötigten Seitenlängen sind:
Für die Höhe des Dreiecks gilt 
Der Flächeninhalt der Grundfläche ist also:
![\(\begin{array}[t]{rll}
A_G &=& |\overrightarrow{AB} | \cdot |\overrightarrow{AD} | + \frac{1}{2}\cdot |\overrightarrow{AD}|\cdot h_{ADE} \\[5pt]
&=& 12\cdot 7 + \frac{1}{2}\cdot 7\cdot 4 \\[5pt]
&=& 98\,[\text{dm}^2]
\end{array}\)](https://mathjax.schullv.de/cc22eab53a60ecf7b1772e5e355e9d232893b455964162b72404f638e7c054cf?color=5a5a5a)
2. Schritt: Volumen berechnen
Anhand der Koordinaten der Punkte ergibt sich die Höhe des Prismas zu 
Das Fassungsvermögen der Schuttmulde beträgt ca. 
4.3.1
Länge der Stange berechnen
Die Länge der Stange folgt mit:
Umrechnen in 
Die Stange ist ca. 
lang.
Neigungswinkel berechnen
Der Neigungswinkel der Stange gegenüber dem Muldelboden entspricht dem Schnittwinkel der Gerade durch und 
mit der 
-Ebene.
Ein Richtungsvektor dieser Gerade ist 
Ein Normalenvektor der -Ebene ist 
![\(\begin{array}[t]{rll}
\sin \beta &=& \dfrac{\pmatrix{10\\12\\3,5}\circ \pmatrix{0\\0\\1}}{\left| \pmatrix{10\\12\\3,5}\right|\cdot \left|\pmatrix{0\\0\\1}\right|} \\[5pt]
\sin \beta &=& \dfrac{10\cdot 0 + 12\cdot 0 + 3,5\cdot 1}{\dfrac{5\sqrt{41}}{2}} \\[5pt]
\sin \beta &=& \dfrac{7}{5\sqrt{41}}\quad \scriptsize \mid\;\sin^{-1} \\[5pt]
\beta &\approx & 12,63^{\circ}
\end{array}\)](https://mathjax.schullv.de/236b315a8e22ea0fc67b37937ad21aedfc355d11f0d53f5f44f16139c8b58b6d?color=5a5a5a)
Der Neigungswinkel der Stange gegenüber dem Muldenboden ist ca. 
groß.
4.3.2
Der Blick in Richtung des oberen Stangenendes lässt sich durch die Gerade 
beschreiben:
Die einzige Seitenwand, die den Blick stören könnte, ist die, die durch beschrieben wird und in der -Ebene liegt. Es wird also der Schnittpunkt der Geraden mit der -Ebene bestimmt.
Für die -Ebene gilt 
Für die Punkte auf der Geraden gilt 
Gleichsetzen:
![\(\begin{array}[t]{rll}
-10+20t &=& 0 &\quad \scriptsize \mid\;+10 \\[5pt]
20t &=& 10 &\quad \scriptsize \mid\; :20 \\[5pt]
t &=& 0,5
\end{array}\)](https://mathjax.schullv.de/585ea916a11be1ae88d2079f674fc1c09b6693a249c915bc0fe385f018c8b9d1?color=5a5a5a)
Einsetzen in die Geradengleichung:
Die höchste 
-Koordinate der Seitenwand ist 
Da 
ist, kann die Fahrerin das obere Ende der Stange also sehen.
4.4
Die Schuttmulde muss so angekippt werden, dass im Modell die Gerade durch die Punkte 
und 
parallel zur 
-Achse verläuft. Es wird der Winkel 
bestimmt, den die Gerade durch die Punkte und mit der Gerade durch die Punkte 
und 
einschließt. Um diesen Winkel muss die Schuttmulde angekippt werden.