Analysis

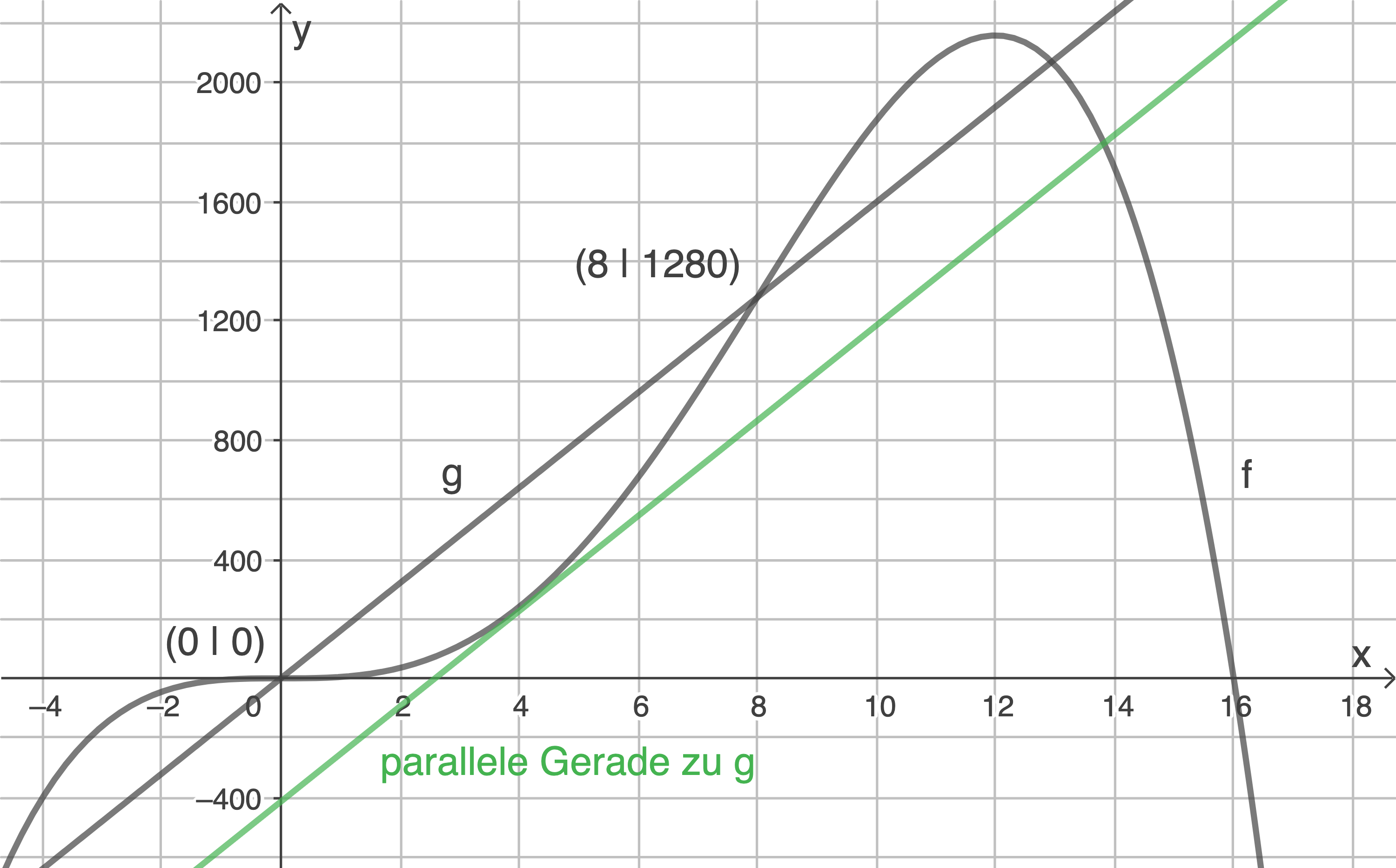
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=-\dfrac{5}{16}x^4 +5x^3.$

Graph einer Funktion mit einer grünen Kurve, die positive und negative Werte zeigt. Achsen beschriftet mit x und y.

1.1

Zeige rechnerisch, dass der Punkt $\left(12 \mid 2160\right)$ ein Hochpunkt des Graphen von $f$ ist und dass die Tangente an den Graphen von $f$ im Punkt $(0 \mid 0)$ parallel zur $x$ -Achse verläuft.

(5 BE)

1.2

Bestimme eine Gleichung der Gerade $g$ , die durch die beiden Wendepunkte des Graphen von $f$ verläuft.
Zeichne in die Abbildung eine Gerade ein, die parallel zu $g$ ist und für $0\leq x \leq 8$ mit dem Graphen von $f$ genau einen Punkt gemeinsam hat.

(7 BE)

1.3

Für jede reelle Zahl $a$ ist eine in $\mathbb{R}$ definierte Funktion $h_a$ mit $h_a (x) = 5ax^2$ gegeben.

1.3.1

Beschreibe, wie der Graph von $h_4$ aus dem Graphen von $h_3$ erzeugt werden kann.

(2 BE)

1.3.2

Bestimme denjenigen Wert von $a$ , für den der Punkt $(4 \mid f (4))$ auf dem Graphen von $h_a$ liegt.

(2 BE)

1.3.3

Es gibt genau einen positiven Wert von $a$ , für den die Graphen von $f$ und $h_a$ genau zwei gemeinsame Punkte haben. Ermittle diesen Wert von $a$ .

(5 BE)

1.3.4

Die Gleichung $f(x) = h_{3,75}(x)$ hat genau die drei Lösungen: $x_1 = 0$ , $x_2 = 6$ und $x_3 = 10$
und es gilt $\displaystyle\int_{0}^{10} ( f (x) - h_{3,75} (x)) dx = 0.$
Deute dies mit Bezug auf die Graphen von $f$ und $h_{3,75}.$

(3 BE)

1.4

Ein Unternehmen lagert Glyzerin in einem Tank. Die momentane Änderungsrate des Tankinhalts kann für $0 \leq x \leq 20$ mithilfe der Funktion $f$ beschrieben werden.
Dabei ist $x$ die seit Beobachtungsbeginn vergangene Zeit in Stunden und $f( x)$ die momentane Änderungsrate in Kilogramm pro Stunde. Zu Beobachtungsbeginn befinden sich im Tank $1200 \,\text{kg}$ Glyzerin.

1.4.1

Der Punkt $( 4 \mid 240)$ liegt auf dem Graphen von $f$ . Interpretiere die Koordinaten dieses Punkts im Sachzusammenhang.

(2 BE)

1.4.2

Beurteile die folgende Aussage:

Zwölf Stunden nach Beobachtungsbeginn ist die größte Menge Glyzerin im Tank enthalten.

(2 BE)

1.4.3

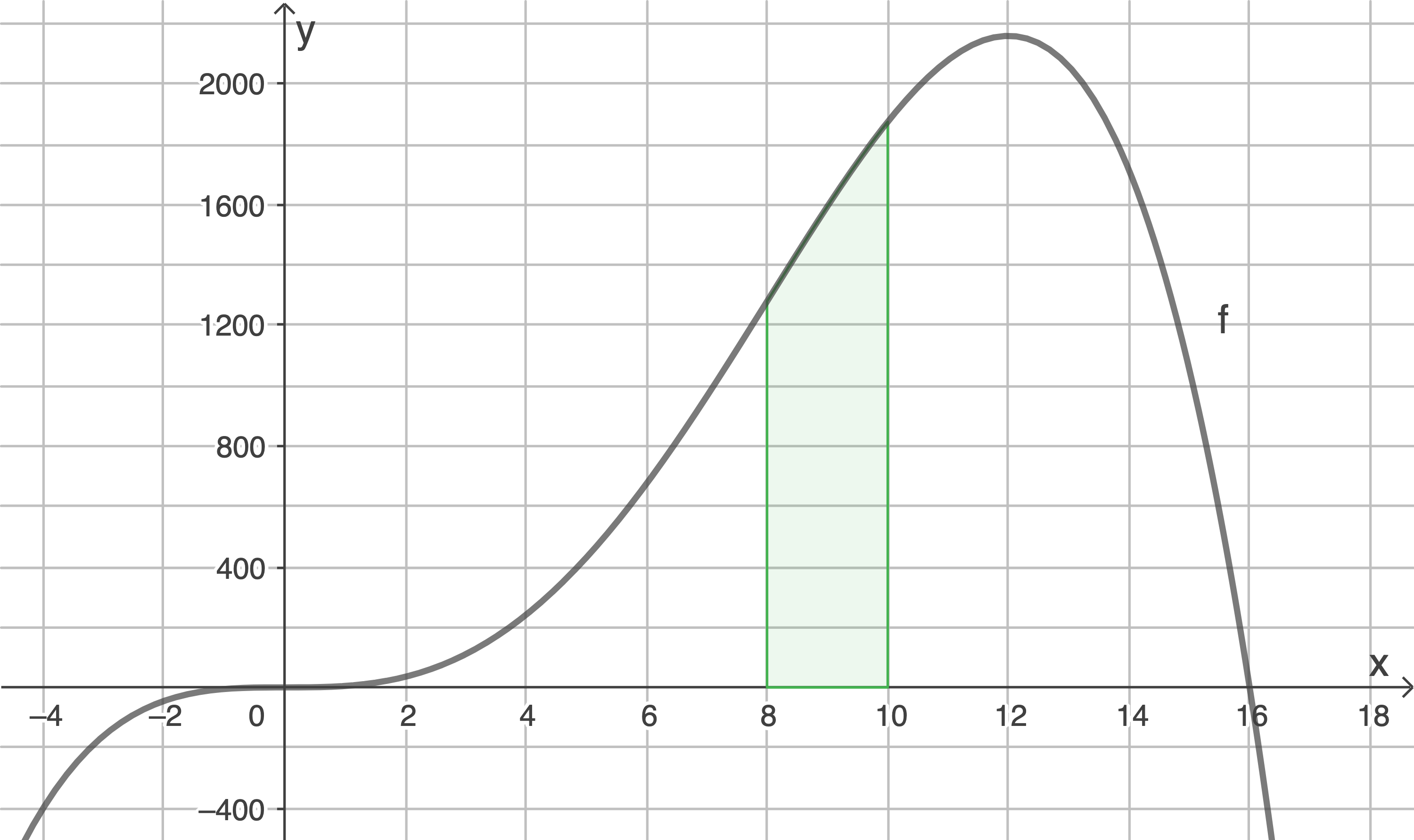
Bestimme grafisch die Zunahme des Tankinhalts zwischen den Zeitpunkten acht Stunden und zehn Stunden nach Beobachtungsbeginn.

(3 BE)

1.4.4

Berechne, wie viel Glyzerin 20 Stunden nach Beobachtungsbeginn im Tank enthalten ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

1. Schritt: Die erste und zweite Ableitung bilden.

Erste Ableitung:

$\(\begin{array}[t]{rll} f$

Zweite Ableitung:

$\(\begin{array}[t]{rll} f$

2. Schritt: Beweisen, dass es sich um einen Hochpunkt handelt.

2.1. Schritt: Vermeintlichen Hochpunkt ablesen.
$f(12)=2160$

2.2. Schritt: Notwendige Bedingung überprüfen.
$\(\begin{array}[t]{rll} 0 &=& f$

2.3. Schritt: Hinreichende Bedingung überprüfen.
$\(\begin{array}[t]{rll} f$
$\(f$ ist $\lt0$ und damit ein Hochpunkt.

3. Schritt: Beweisen, dass die Tangente parallel zur x-Achse verläuft.

Damit die Tangente bei $\left(0\mid0\right)$ parallel zur x-Achse verläuft, muss folgendes gelten:

$\(\begin{array}[t]{rll} 0&=& f$

Da $\(f$ , verläuft die Tangente an den Graphen von f im Punkt $\left(0\mid0\right)$ parallel zur x-Achse.

1.2

1. Schritt: Wendepunkte bestimmen

Mit der notwendigen Bedingung für Wendepunkte folgt:

$\(\begin{array}[t]{rll} 0&=& f$

Damit folgt:

$x_1 = 0$

$\begin{array}[t]{rll} 0&=& -\dfrac{15}{4}x+30 &\quad \scriptsize \mid\; - 30 \\[5pt] -30&=& -\dfrac{15}{4}x & \quad \scriptsize \mid\; \cdot \left( - \frac{4}{15} \right) \\[5pt] 8& =& x_2& \end{array}$

Überprüfen der notwendigen Bedingung:

$\( f$

Damit gilt für die Wendepunkte: $W_1 (0 \mid f(0)) = W_1 (0 \mid 0)$ und $W_2 (8 \mid f(8)) = W_2 (8 \mid 1280)$ .

2. Schritt: Gerade bestimmen.

Die Formel für eine allgemeine Gerade lautet: $g(x) = mx + c$ .

Durch Einsetzen der bekannten Wendepunkte, lassen sich $m$ und $c$ bestimmen:

$\begin{array}[t]{rll} g(0)&=& 0&\quad \scriptsize \\[5pt] m \cdot 0 + c&=& 0& \quad \scriptsize \\[5pt] c & = & 0& \end{array}$

$\begin{array}[t]{rll} g(8)&=& 1280&\quad \scriptsize \\[5pt] m \cdot 8 + 0&=& 1280& \quad \scriptsize \mid\; :8 \\[5pt] m& =& 160& \end{array}$

Damit lautet die Geradengleichung $g(x)=160x$ .

3. Schritt: Geraden einzeichnen.

Mit Hilfe der Wendepunkte lässt sich die Gerade $g$ einzeichnen. Anhand von ihr kann die zu $g$ gesuchte parallele Gerade eingezeichnet werden.

Grafik mit zwei Funktionen und einer parallelen Linie, die die Achsen x und y zeigt.

1.3

1.3.1

$\begin{array}[t]{rll} h_4(x)&=& h_3(x)\cdot b& \quad \scriptsize \\[5pt] 5\cdot4\cdot x^2&=& 5\cdot3\cdot x^2\cdot b& \quad \scriptsize \mid \text{kürzen}\\[5pt] 4&=& 3\cdot b& \quad \scriptsize \mid :3\\[5pt] b&=& \dfrac{4}{3}& \quad \scriptsize \\[5pt] \end{array}$

$h_4$ entsteht, wenn $h_3$ mit dem Faktor $\frac{4}{3}$ in $y$ -Richtung gestreckt wird.

1.3.2

$\begin{array}[t]{rll} h_a(4)&=& f(4)& \quad \scriptsize \\[5pt] 5a \cdot 4^2 &=& -\dfrac{5}{4}\cdot 4^3+15\cdot 4^2 & \quad \scriptsize \\[5pt] 5a \cdot 16&=& 240 & \quad \scriptsize \\[5pt] a \cdot 80&=& 240 \qquad \scriptsize \mid :80\\[5pt] a &=& 3 & \quad \scriptsize \\[5pt] \end{array}$

Für $a = 3$ liegt der Punkt $(4 \mid f(4))$ auf dem Graphen von $h_a$ .

1.3.3

Vollständigen Rechenweg anzeigen

$-\dfrac{5}{16}x^2\cdot\left(x^2-16x+16a\right)= 0$

Mit dem Satz des Nullprodukts folgt $x_{1}=0.$ Des Weiteren folgt:

$x_{2, 3}= 8\pm\sqrt{64-16a}$

Vollständige Lösung anzeigen

Damit nur genau zwei Schnittpunkte existieren, muss $x_2=x_3$ gelten. Das ist genau dann der Fall, wenn die Wurzel im oberen Ausdruck gleich $0$ ist. Also gilt:

$\begin{array}[t]{rll} 64-16a&=& 0 & \quad \scriptsize \mid+16a\\[5pt] 16a&=& 64 & \quad \scriptsize \mid:16\\[5pt] a&=& 4 & \quad \scriptsize \\[5pt] \end{array}$

Für $a = 4$ haben die Graphen $f$ und $h_a$ genau zwei gemeinsame Punkte.

1.3.4

Die drei Lösungen entsprechen den drei gemeinsamen Punkten von $h_{3,75}$ und dem Graphen $f$ und schließen damit zwei Flächenstücke gleichen Inhalts ein. Da das Integral 0 ergibt, liegen diese Flächenstücke auf verschiedenen Seiten des Graphen von $h_{3,75}$ .

1.4.1

Die Änderungsrate des Tankinhalts beträgt vier Stunden nach Beobachtungsbeginn $240 \, \frac{\text{km}}{\text{h}}$ .

1.4.2

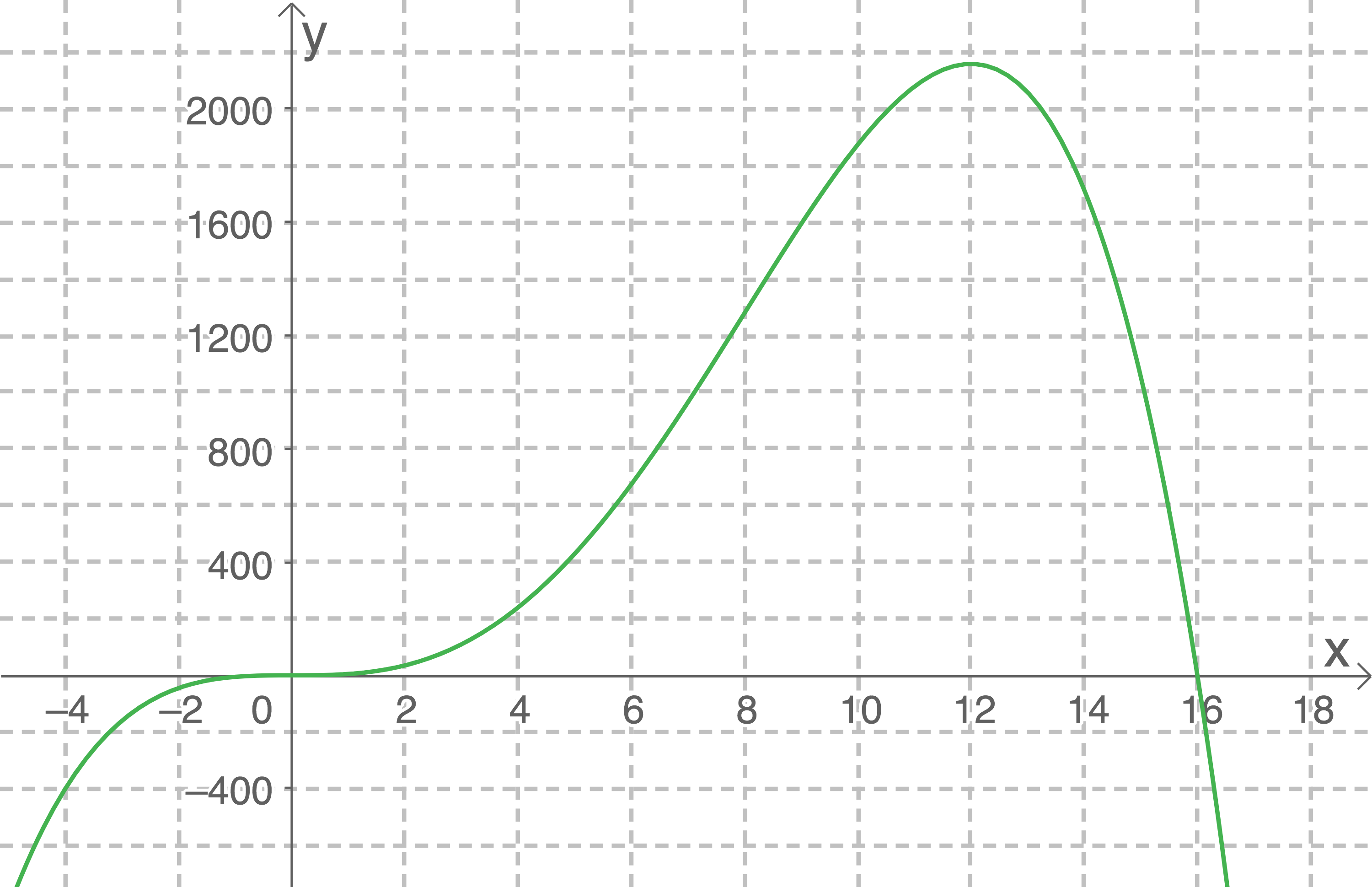
Zwölf Stunden nach Beobachtungsbeginn ist die momentane Änderungsrate positiv. Solange die Änderungsrate positiv ist nimmt die Menge Glyzerin zu. In der Zeit von $12$ h bis $16$ h nimmt die Menge Glyzerin immer langsamer zu, weil die Änderungsrate sinkt, aber sie nimmt zu. Die größte Menge Glyzerin befindet sich im Tank, bevor die Änderungsrate negativ wird. Das ist bei $16$ h, wenn der Graph die x-Achse schneidet, der Fall.
Damit ist die Aussage falsch.

1.4.3

Grafik einer Funktion f mit Kurvenverlauf und einem hervorgehobenen Bereich zwischen x=8 und x=10.

Die Inhaltszunahme entspricht ungefähr $8\cdot2\cdot 200$ kg $=3200$ kg.

1.4.4

$\begin{array}[t]{rll} && \int \limits_{0}^{20}f(x)dx& \quad \scriptsize \\[5pt] &=&\left[-\dfrac{1}{16}x^5+\frac{5}{4}x^4 \right]_{0}^{20}& \quad \scriptsize \\[5pt] &=& -\dfrac{1}{16}\cdot 20^5+\dfrac{5}{4}\cdot 20^4 & \quad \scriptsize \\[5pt] &=& -200\,000+200\,000 & \quad \scriptsize \\[5pt] &=& 0 & \quad \scriptsize \\[5pt] \end{array}$

$20$ Stunden nach Beobachtungsbeginn befindet sich genauso viel Glyzerin im Tank wie zu Beobachtungsbeginn. Es befinden sich $1200$ kg Glyzerin im Tank.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?