Wahlteil A3
A3 Analysis und Stochastik
3.1
Gegeben ist die Funktion 
mit 
mit 
3.1.1
Gib eine Gleichung der Ableitungsfunktion 
von an.
Zeichne die Graphen von und in ein gemeinsames Koordinatensystem.
Zeichne die Graphen von
(3 BE)
3.1.2
Berechne den Wert für 
für den die Differenz 
maximal wird.
Hinweis: 
mit 
(5 BE)
3.1.3
Es existiert eine quadratische Funktion 
mit folgenden Eigenschaften:
- Die Funktionen
- Die Graphen von
(5 BE)
3.2
Gegeben ist eine Schar von Funktionen durch die Gleichung 
mit 
Die Ableitungsfunktion
hat die Gleichung 
Die Graphen heißen
Die Graphen der Ableitungsfunktionen von 
heißen 
Die Ableitungsfunktion
Die Graphen heißen
3.2.1
Zeichne 
und 
im Intervall 
in ein gemeinsames Koordinatensystem.
(2 BE)
3.2.2
Für jeden Wert von 
begrenzen 
und die 
-Achse im Intervall eine Fläche 
vollständig.
Berechne den Inhalt der Fläche in Abhängigkeit von 
teilt die Fläche in zwei Teilflächen.
Weise nach, dass das Verhältnis der Inhalte dieser Teilflächen unabhängig von ist.
Gib das Verhältnis der Teilflächen an.
Gib das Verhältnis der Teilflächen an.
(12 BE)
3.3
Ein Lottospieler gibt genau einen Tipp für die Lotterie 
aus 
ab. Dafür muss er 
verschiedene Zahlen von 
bis 
tippen.
Für diese Lotterie werden Kugeln jeweils mit einer der Zahlen bis beschriftet, wobei jede Zahl nur einmal vorkommt. Es werden Kugeln zufällig ohne Zurücklegen gezogen und deren Beschriftung notiert.
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
Der Lottospieler hat
alle fünf Zahlen richtig getippt,
keine Zahl richtig getippt,
mehr als drei Zahlen richtig getippt.
Abweichend vom oben beschriebenen Vorgehen wird unter sonst gleichen Bedingungen die gezogene Kugel jeweils wieder zurückgelegt.
Berechne die Wahrscheinlichkeit dafür, ein Ziehungsergebnis mit fünf gleichen Zahlen zu erhalten.
Für diese Lotterie werden
(8 BE)
3.1.1
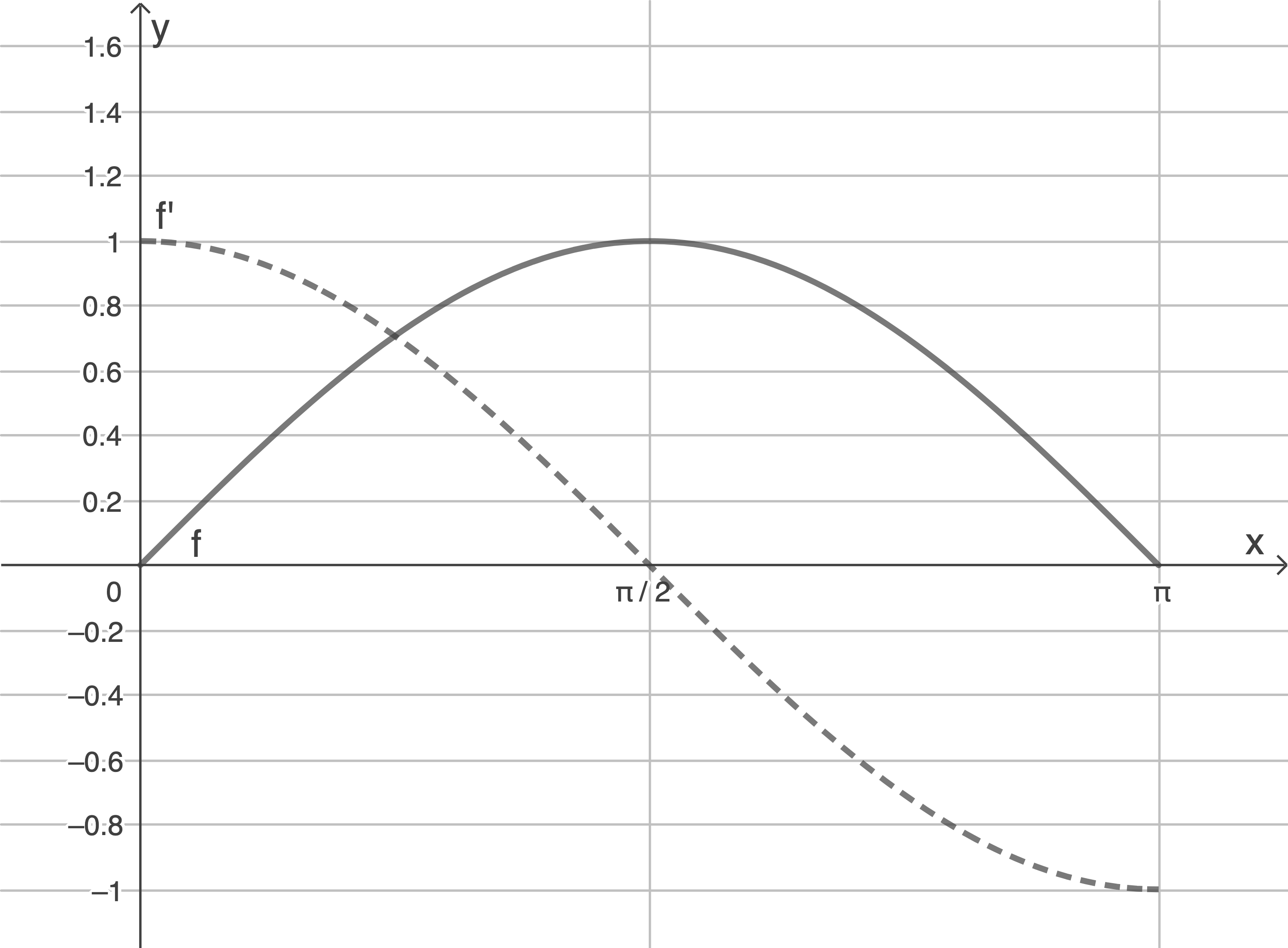
3.1.2
Extremwertproblem:
Ableitungen:
Notwendige Bedingung für lokale Extrema:
Hinreichende Bedingung für lokale Extrema:
Lokales Maximum:
Globales Maximum:
Durch 
und 
wird berechnet, dass die Definitionsbereiche von 
und identisch sind, daraus ergibt sich:
lokales Maximum = globales Maximum
Maximale Differenz: 
Die Berechnung der maximalen Differenz ist nicht erforderlich.
Vollständige Lösung anzeigen
3.1.3
Quadratische Funktion: 
Nullstellen von :
Also:
![\(\begin{array}[t]{rll}
a\pi^2 + b\pi&=&0 &\quad \scriptsize \mid\;-a\pi^2\mid\;:\pi \\[5pt]
b&=&-a\pi
\end{array}\)](https://mathjax.schullv.de/20ee639ce03985911d762abe31208fb939a2122796b47a11c59e50021d10e854?color=5a5a5a)
Hochpunkt von : 
![\(\begin{array}[t]{rll}
g\left(\dfrac{\pi}{2}\right)&=& 1&\quad \scriptsize \; \\[5pt]
a\left(\dfrac{\pi}{2}\right)^2 - a\pi \left(\dfrac{\pi}{2}\right) &=& 1&\quad \scriptsize \; \\[5pt]
- \dfrac{\pi^2}{4}a&=& 1&\quad \scriptsize \mid\;:(- \frac{\pi^2}{4}) \\[5pt]
a&=& - \dfrac{4}{\pi^2}
\end{array}\)](https://mathjax.schullv.de/822cc0daed6fbb7550c388794c05dd24fb8e0eece96f176dfc3336ef455405ac?color=5a5a5a)
3.2.1
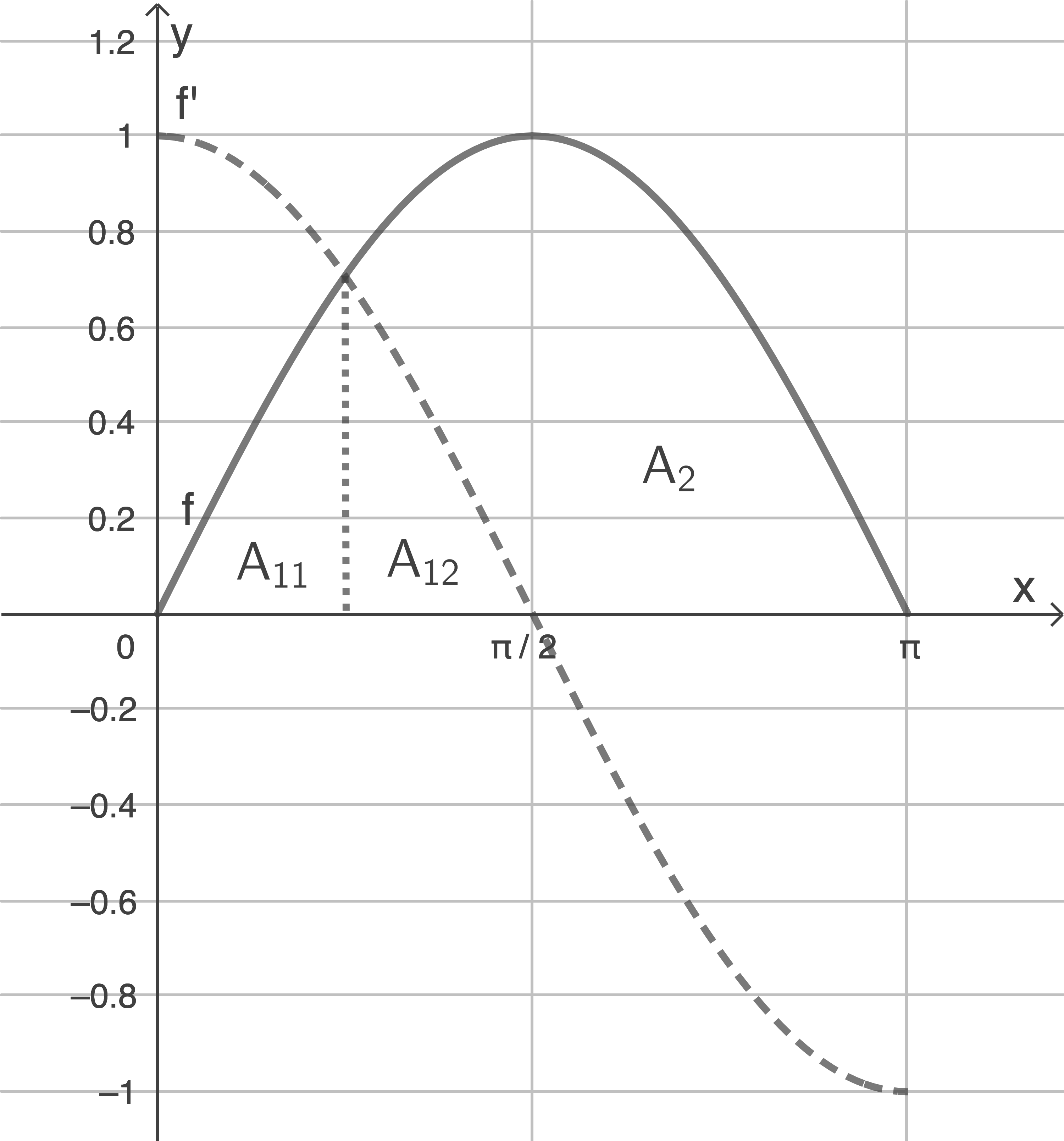
3.2.2
Flächeninhalt:
![\(A= \displaystyle\int_{0}^{\pi}f_a(x)\mathrm dx = \left[-a \cdot \cos(x)\right]_0^\pi = (a-(-a)) = 2a\)](https://mathjax.schullv.de/777f3ac7bf575d4399dc613b164c71f87cdd28720800ec9bb0aa01ba428c0379?color=5a5a5a)
Berechnung des Inhalts einer Teilfläche, wie in 3.2.1 verdeutlicht:
Schnittstelle von und 
![\(\begin{array}[t]{rll}
a \cdot \sin x&=& a \cdot \cos x &\quad \scriptsize \mid\;:a \cdot \cos x \\[5pt]
\tan x&=& 1&\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
x&=& \dfrac{\pi}{4}&\quad \\[5pt]
\end{array}\)](https://mathjax.schullv.de/71beb8cba0aa62fd1475a2a97793a025813e74b67a5e3de82852c284573bf354?color=5a5a5a)
![\(\begin{array}[t]{rll}
A_1&=&A_{11}+ A_{12} &\quad \scriptsize \; \\[5pt]
&=&\displaystyle\int_{0}^{\frac{\pi}{4}}f_a(x)\mathrm dx + \displaystyle\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}f_a](https://mathjax.schullv.de/41cae5556ccf3a0527fd90da0f7274d9f99eaab12e100c975d323c8f0415dc64?color=5a5a5a)
Berechnung des Inhalts der zweiten Teilfläche:
Verhältnis der Inhalte der Teilflächen:
Damit ist das Verhältnis der Flächen unabhängig vom Parameter
3.3