Wahlaufgaben

5 Analysis

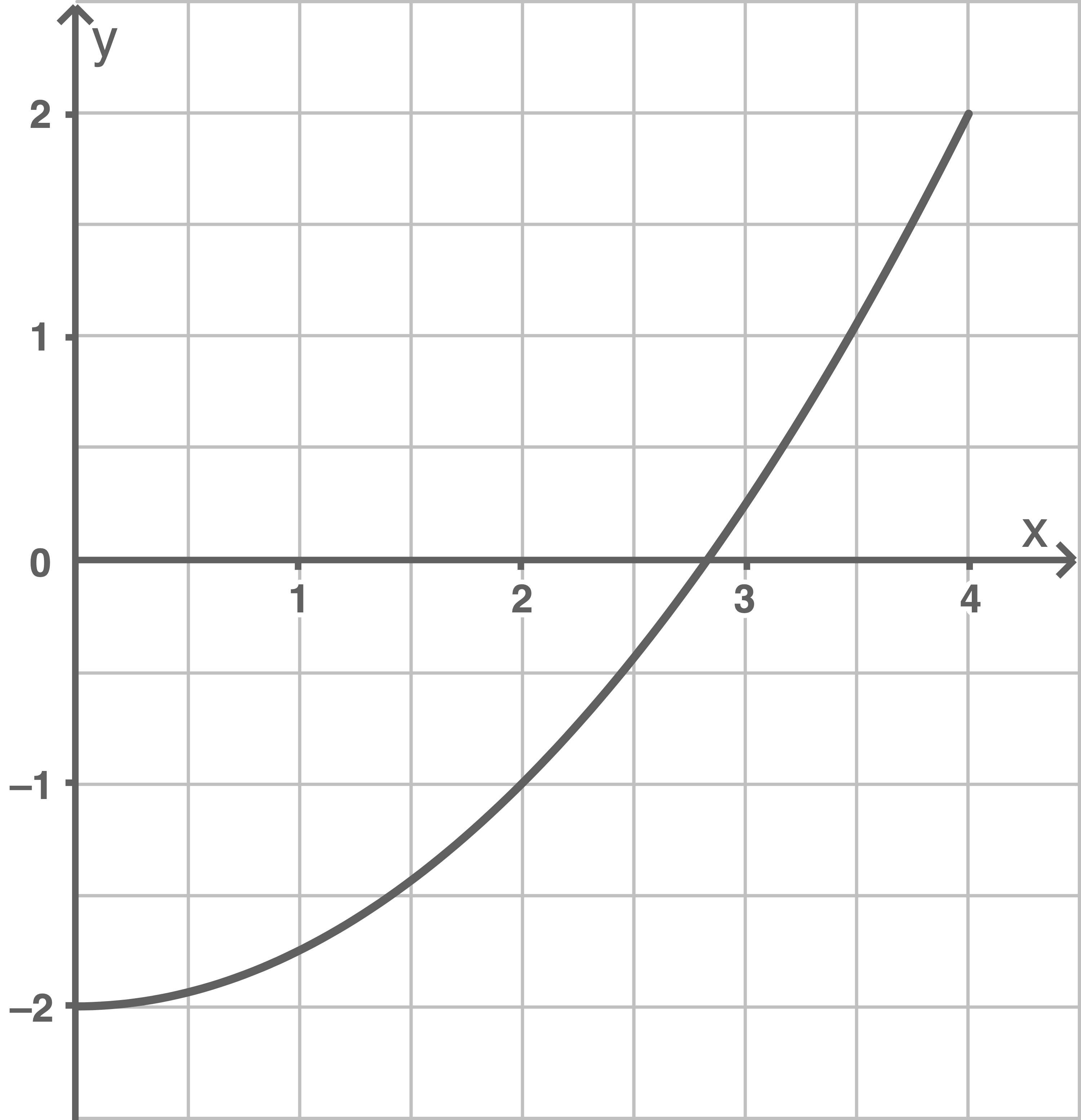
Gegeben ist der Graph einer Funktion $f$ mit $0 \leq x \leq 4 ; x \in \mathbb{R}$ .
Betrachtet werden Intervalle $[a ; b],$ in denen die Funktion $f$ dieselbe mittlere Änderungsrate wie im Intervall $[0 ; 4]$ hat.

5.1

Bestimme für $a=1$ graphisch den Wert von $b.$

(2 BE)

5.2

Begründe, dass es nicht für jeden Wert von $a$ ein solches Intervall $[a ; b]$ gibt.

(3 BE)

6 Analysis

Gegeben ist die Funktion $f$ durch die Gleichung $f(x)=-\mathrm e^x+2$ mit $x \in \mathbb{R}.$

6.1

Beschreibe, wie der Graph von $f$ aus dem Graphen von $g$ mit der Gleichung $g(x)=\mathrm e^x$ hervorgeht.

(2 BE)

6.2

Betrachtet werden die Funktionen $h_a$ mit $h_a(x)=a \cdot f(x)$ und $a \in \mathbb{R},$ $a>0.$
Ermittle den Wertebereich von $h_a$ in Abhängigkeit von $a.$

(3 BE)

7 Analytische Geometrie

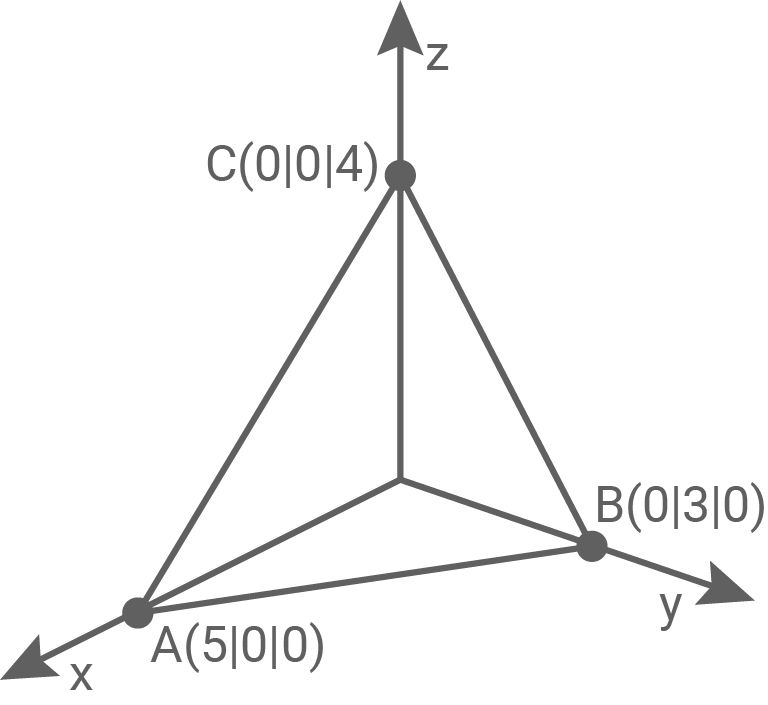
Die Abbildung zeigt das Dreieck $ABC$ .
Der Koordinatenursprung wird mit $O$ bezeichnet.

Dreieck im dreidimensionalen Koordinatensystem - MV Abi 2023

7.1

Die Ebene, in der das Dreieck $ABC$ liegt, kann durch eine Gleichung der Form $12 x+20 y+t z=60$ dargestellt werden. Bestimme den Wert von $t.$

(1 BE)

7.2

Für jeden Wert von $k$ mit $k \in [-3 ; 5]$ wird die Pyramide $OA_k B_k C$ mit $A_k(5-k \mid 0 \mid 0)$ und $B_k(0 \mid 3+k \mid 0)$ betrachtet. Bestimme denjenigen Wert von $k$ , für den die Pyramide das größte Volumen hat.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

5 Analysis

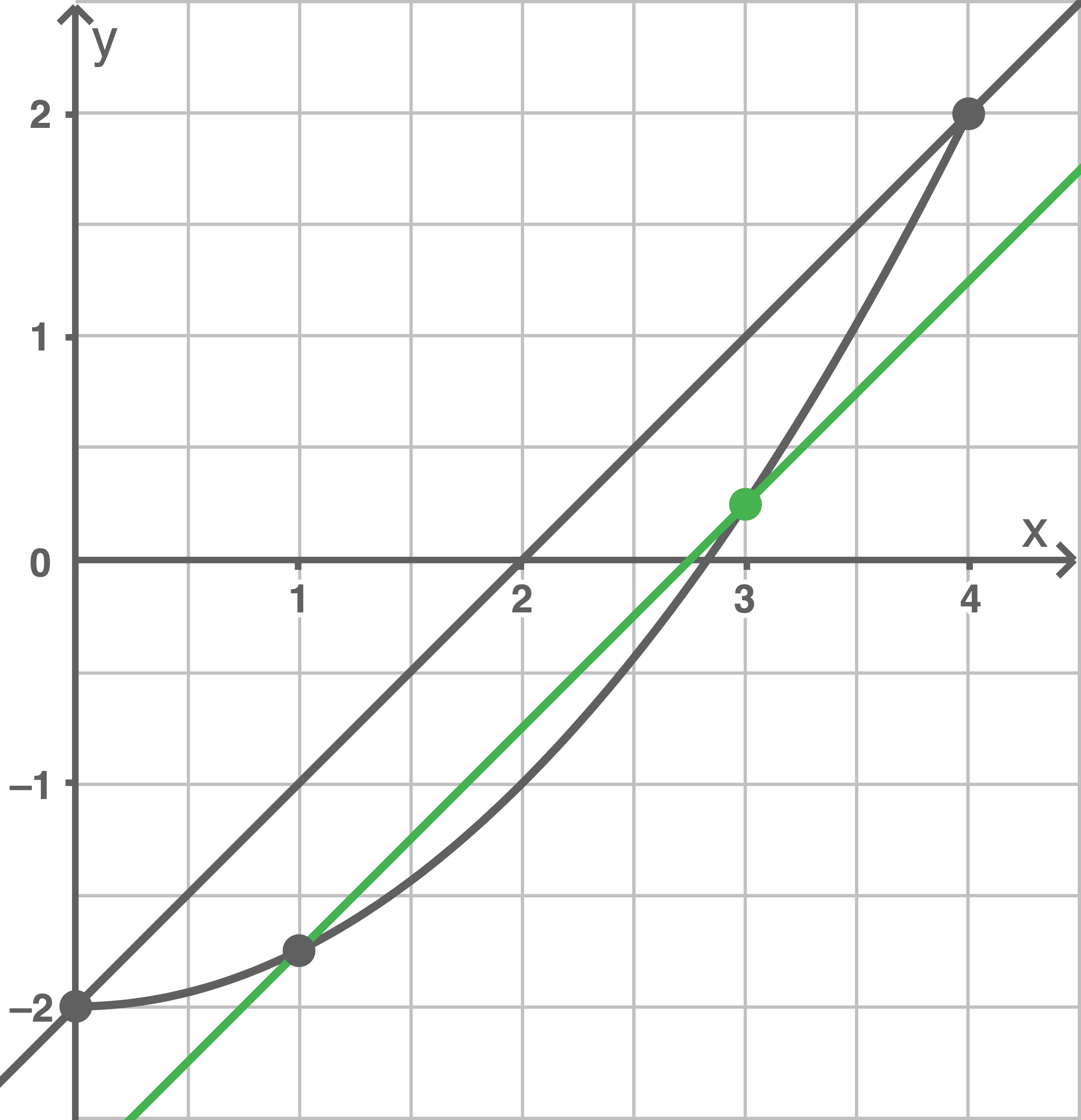
5.1

Gerade $g$ durch die Punkte $(0\mid f(0))$ und $(4\mid f(4))$ einzeichnen
Punkt $A(1\mid f(1))$ einzeichnen
Zu $g$ parallele Gerade durch $A$ einzeichnen
Schnittstelle der Parallelen mit dem Graph von $f$ ist $b.$

Es ergibt sich $b=3.$

5.2

Im Intervall $[0;4]$ besitzt $f$ die mittlere Änderungsrate $1.$
Die Tangente an den Graphen von $f$ hat an der Stelle $x=2$ den Anstieg $1.$ Für $x\gt 2$ gilt $\(f$
Folglich ist auch die mittlere Änderungsrate für alle Intervalle mit $a\gt 2$ größer als $1.$ Für $a\gt 2$ gibt es daher keines der beschriebenen Intervalle.

6 Analysis

6.1

Der Graph von $g$ wird an der $x$ -Achse gespiegelt und anschließend um zwei Einheiten in positive $y$ -Richtung verschoben.

6.2

$h_a(x) = a\cdot f(x) = a \cdot \left(-\mathrm e^x +2 \right)$ $= -a\cdot \mathrm e^x +2a$

Für die einzelnen Summanden gilt:

$\lim\limits_{x\to\infty} \left(-a\cdot \mathrm e^x\right) = -\infty$

$\lim\limits_{x\to-\infty} \left(-a\cdot \mathrm e^x\right) = 0$

$\lim\limits_{x\to\pm\infty} \left(2a\right)= 2a$

Die Gerade $y=2a$ ist demnach eine waagerechte Asymptote an den Graphen von $h_a.$ Da alle Graphen von $h_a$ monoton fallend sind, folgt für den Wertebereich:

$\left\{h_a(x) \in \mathbb{R} \mid h_a(x)\lt 2 a\right\}.$

7 Analytische Geometrie

7.1

In die Ebenengleichung müssen die Koordinaten eines Punktes eingesetzt werden, dessen $z$ -Koordinate nicht $0$ ist. Sonst würde der einzige Summand mit $t$ wegfallen. Daher werden die Koordinaten von $C$ eingesetzt:

$\begin{array}[t]{rll} 12\cdot 0 + 20\cdot 0 +t\cdot 4 &=& 60 \\[5pt] 4t &=& 60 &\quad \scriptsize \mid\; :4\\[5pt] t &=& 15 \end{array}$

7.2

Die Grundfläche der Pyramide ist das rechtwinklige Dreieck $OAB,$ die Höhe der Pyramide $|\overrightarrow{OC}|=4.$

Das Volumen ist am größten, wenn der Inhalt der Grundfläche $OAB$ maximal ist:

Rechenweg anzeigen

$A_{OAB} = 7,5 +k -0,5k^2$

$A_{OAB}$ lässt sich in Abhängigkeit von $k$ als nach unten geöffnete Parabel darstellen. Die Stelle des Scheitelpunkts (Hochpunkt) entspricht dem Wert von $k,$ für den der Flächeninhalt am größten ist.
Die Nullstellen lassen sich aus dem Term von $A_{O A B}=\frac{(5-k) \cdot(3+k)}{2}$ ablesen und lauten $k_1=5$ und $k_2=-3.$
Der Scheitelpunkt liegt in der Mitte zwischen den beiden Nullstellen. Somit ist der Flächeninhalt $A_{O A B}$ und damit auch das Volumen der Pyramide für $k=\frac{-3+5}{2}=1$ maximal.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?