1 Analysis
Gegeben ist eine ganzrationale Funktion 3. Grades. Der Graph dieser Funktion 
ist punktsymmetrisch zum Koordinatenursprung und hat im Punkt 
einen lokalen Extrempunkt.
1.1
Ermittle eine Gleichung dieser Funktion.
(Zur Kontrolle: 
)
(3 BE)
1.2
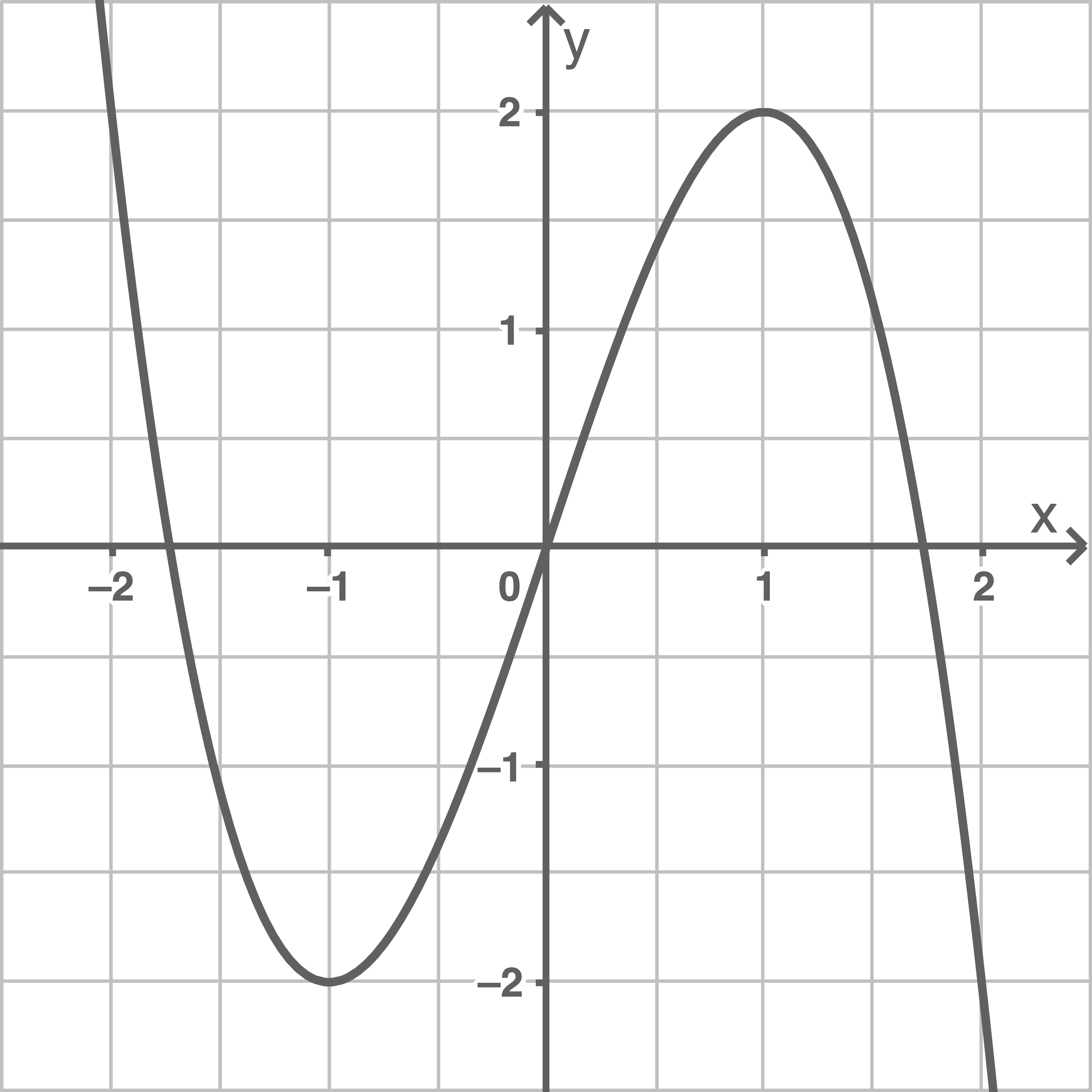
Gib die Koordinaten des zweiten Extrempunktes des Graphen von an und skizziere den Graphen von mindestens im Intervall ![\([-2 ; 2].\)](https://mathjax.schullv.de/2c6ce6671d288838cc6081a35e75b6157e540801c0ea94c00c0340ea9b914471?color=5a5a5a)
(3 BE)
1.3
Berechne den Anstieg der Normale an den Graphen von an der Stelle 
.
(2 BE)
1.4
Beurteile folgende Aussage: 
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Aufgrund der Punktsymmetrie des Graphen zum Koordinatenursprung hat die Funktionsgleichung von folgende Form:
mit
Aus dem Aufgabentext folgt weiterhin:
![\(\begin{array}{lrll}
\text{I}\quad& f(1) &=& 2 \\[5pt]
& a\cdot 1^3 +c\cdot 1 &=& 2 \\[5pt]
& a +c &=& 2 \\[5pt]
\text{II}\quad& f](https://mathjax.schullv.de/c65b3a8dd2d91f56a647c39104a13a6e0734944e016566ea70bf79b0e06d378f?color=5a5a5a)
Aus 
folgt 
Einsetzen in 
![\(\begin{array}[t]{rll}
a+c &=& 2 &\quad \scriptsize \mid\; c=-3a \\[5pt]
a-3a &=& 2 \\[5pt]
-2a &=& 2 &\quad \scriptsize \mid\; :(-2)\\[5pt]
a &=& -1 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6254d9b4deacd753f4a2521cf03a596d3512eb462c7368d2a6d6ef0d94a96e62?color=5a5a5a)
Daraus folgt:
1.2
Aufgrund der Punktsymmetrie ergeben sich die Koordinaten des zweiten lokalen Extrempunkts durch Spiegelung am Koordinatenursprung zu 
1.3
Der Anstieg der Tangente an den Graphen von an der Stelle 
wird durch die erste Ableitungsfunktion beschrieben:
Die Steigung der Normale an derselben Stelle ergibt sich zu:
1.4
Aufgrund der Punktsymmetrie sind die Flächenstücke, die der Graph von im Intervall ![\([-1; 0]\)](https://mathjax.schullv.de/2a23d9bb4360dfcc8b6f6be9c468f47e0bfae23900fc83f86d7d786b051cf01a?color=5a5a5a)
und ![\([0;1]\)](https://mathjax.schullv.de/67b85eab103aec1314a6a9fe5de4b047f5cd37fb49f90a88e9c8c39a6daa39b6?color=5a5a5a)
mit der -Achse begrenzt, gleich groß.
Eines von beiden liegt unterhalb der-Achse, wodurch das zugehörige Integral ein negatives Vorzeichen hat, das andere liegt oberhalb der -Achse, sodass das zugehörige Integral ein positives Vorzeichen hat.
Daher gilt:
Der Graph zur Funktion 
mit 
geht aus dem Graphen von durch Verschiebung um drei Einheiten in positive -Richtung hervor.
Damit wird auch der Symmetriepunkt entsprechend verschoben und es folgt:
Die Aussage ist also wahr.
Eines von beiden liegt unterhalb der