Pflichtaufgaben

Analysis

Gegeben ist eine in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^3-x$ .

1.1

Einer der folgenden Graphen I, II und III stellt $f$ dar.
Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.

Graph einer mathematischen Funktion mit den Achsen x und y.

Graf einer mathematischen Funktion mit x- und y-Achse, zeigt eine grüne Kurve.

Graph einer Funktion mit x- und y-Achse, zeigt eine steigende Kurve.

(2 BE)

1.2

Berechne den Inhalt der Fläche, die der Graph von $f$ und die $x$ -Achse einschließen.

(3 BE)

Die Abbildung 1 zeigt den Graphen einer in $\mathbb{R}$ definierten Funktion $f$ , die Abbildung 2 den Graphen einer Stammfunktion $F$ von $f$ .

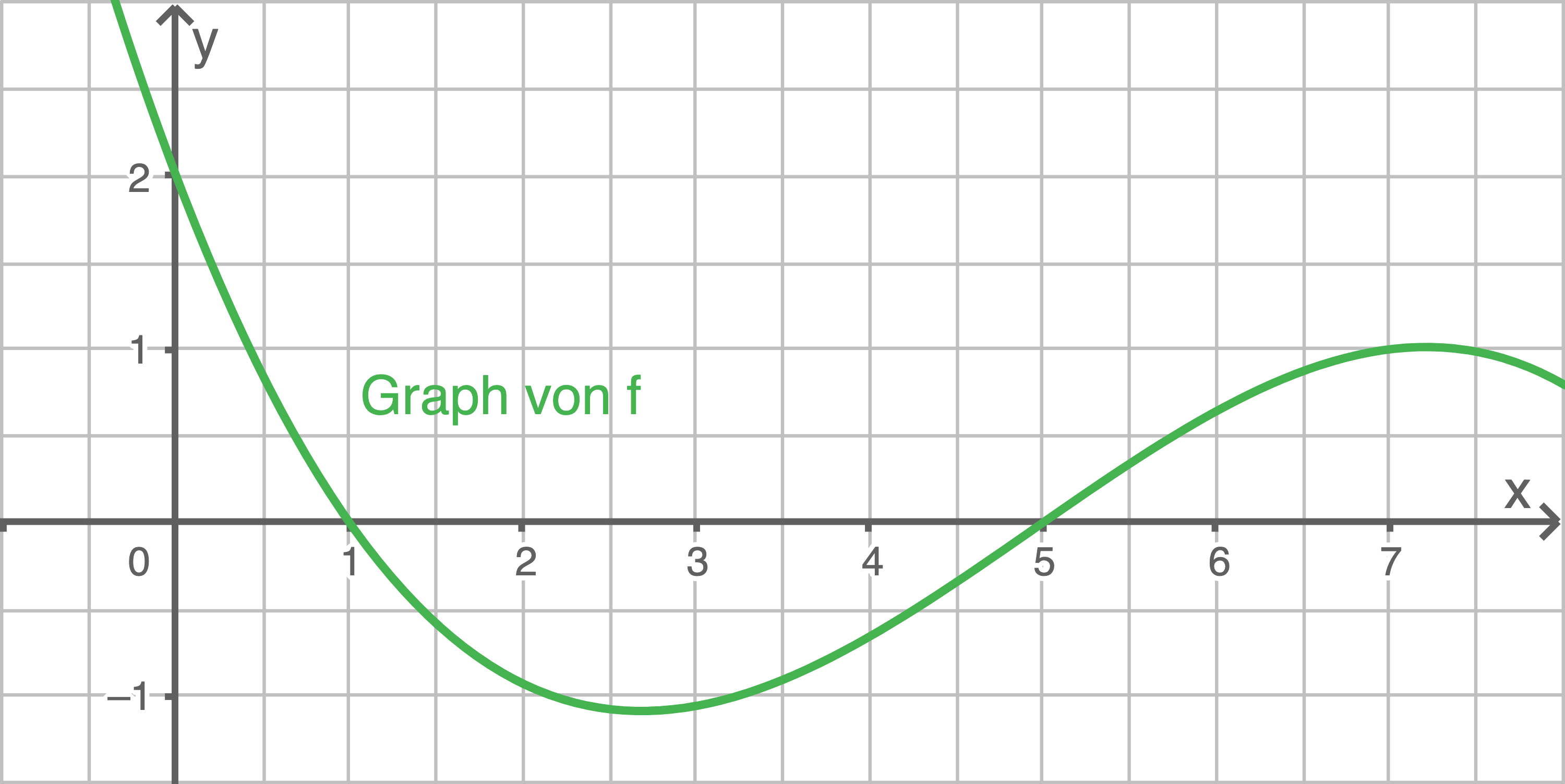
Graph einer Funktion f in einem Koordinatensystem mit Achsenbeschriftung.

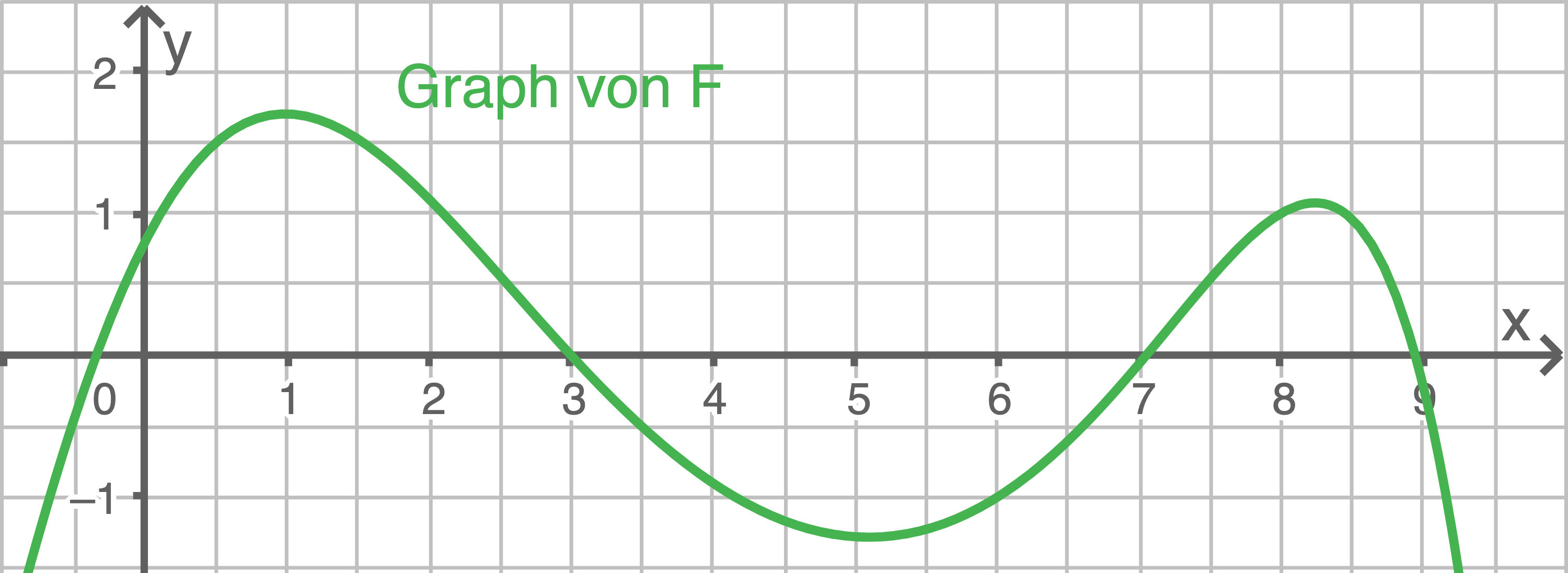
Abbildung 1

Graph von F auf einem Koordinatensystem mit x- und y-Achse.

Abbildung 2

2.1

Bestimme ausschließlich mithilfe der Abbildung 2 den Wert des Terms $\displaystyle\int_{1}^{5}f(x)\mathrm dx.$

(2 BE)

2.2

Beschreibe, wie man den Wert des Terms $\displaystyle\int_{1}^{5}f(x)\mathrm dx$ ausschließlich mithilfe der Abbildung 1 bestimmen könnte.

(3 BE)

Analytische Geometrie

Gegeben sind die Punkte A $\left(5\mid0\mid a\right)$ und B $\left(2\mid4\mid5\right)$ .
Der Koordinatenursprung wird mit O bezeichnet.

3.1

Bestimme denjenigen Wert von $a$ , für den A und B den Abstand 5 haben.

(3 BE)

3.2

Ermittle denjenigen Wert von $a$ , für den das Dreieck OAB im Punkt B rechwinklig ist.

(2 BE)

Stochastik

Im Folgenden werden zwei Würfel stets gemeinsam geworfen. Bei jedem der beiden Würfel sind die Seiten mit den Zahlen von 1 bis 6 durchnummeriert.

4.1

Die beiden Würfel werden einmal geworfen. Begründe, dass die Wahrscheinlichkeit dafür, dass dabei keine „6“ auftritt, $\frac{25}{36}$ beträgt.

(2 BE)

4.2

Die beiden Würfel werden $36$ -mal geworfen. Die binomialverteilte Zufallsgröße $X$ gibt die Anzahl der Würfe an, bei denen keine „6“ auftritt.
Begründe für jede der folgenden Abbildungen, dass sie nicht die Wahrscheinlichkeitsverteilung von $X$ zeigt.

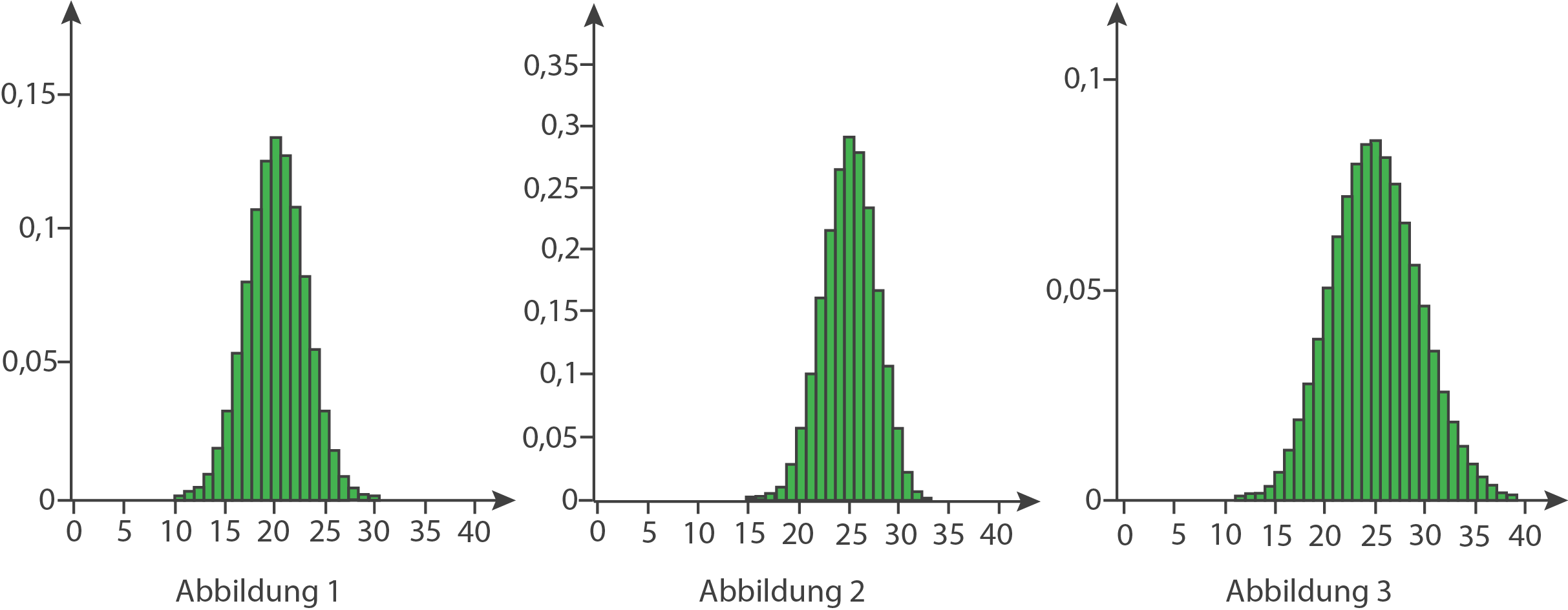
Drei Balkendiagramme mit grünen Säulen und unterschiedlichen Verteilungen auf schwarzem Hintergrund.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Graph $II$ kommt nicht in Frage, da $f(0,5)\lt0$ gilt.
Graph $III$ kommt nicht in Frage, da die Steigung des Graphen von f für $-0,5 \leq x \leq0,5$ nicht konstant ist

1.2

Durch Ablesen am Graphen $I$ oder durch Nachrechnen, lassen sich die Nullstellen von $f$ ermitteln: $x_1 = -1$ und $x_2 = 1$ . Mit der Punktsymmetrie der Funktion $f$ folgt dann:

$\begin{array}[t]{rll} && 2 \cdot \displaystyle\int_{-1}^{0}f(x)\;\mathrm dx& \quad \scriptsize \\[5pt] &=& 2 \cdot \left[\dfrac{1}{4}x^4-\dfrac{1}{2}x^2\right]_{-1}^{0} & \quad \scriptsize \\[5pt] &=& 2 \cdot \left(-\dfrac{1}{4}+\dfrac{1}{2}\right) & \quad \scriptsize \\[5pt] &=& 2 \cdot \dfrac{1}{4} & \quad \scriptsize \\[5pt] &=& \dfrac{1}{2} & \quad \scriptsize \\[5pt] \end{array}$

2.1

Ein Integral wird bestimmt, indem die Stammfunktion der unteren Grenze von der Stammfunktion der oberen Grenze abgezogen wird.
Mit Hilfe der Abbildung $2$ lassen sich die Werte ablesen und das Integral von $f$ berechnen:

$\displaystyle\int_{1}^{5}f(x)\;\mathrm dx = F(5)-F(1) \approx -1,3 - 1,7 = 3$

2.2

Das Integral einer Funktion beschreibt die Fläche unter dem Graphen. Deshalb wäre eine Möglichkeit die Kästchen, im Intervall $1 \leq x\leq 5$ , unter dem Graphen zu zählen. Da ein Kästchen lediglich $\dfrac{1}{4}$ eines Einheitskästchens darstellt, muss die Anzahl der Kästchen mal $0,25$ genommen werden. Weil der Graph unter der x-Achse verläuft, muss zusätzlich mit $-1$ multipliziert werden.

3.1

$\begin{array}[t]{rll} 5 &=& \mid \overrightarrow{AB}\mid & \quad \scriptsize \\[5pt] 5&=& \,\bigg \vert \, \pmatrix{2-5\\4-0\\5-a} \,\bigg \vert \, & \quad \scriptsize \\[5pt] 5 &=&\,\bigg \vert \, \pmatrix{-3\\4\\5-a} \,\bigg \vert \, & \quad \scriptsize \\[5pt] 5&=&\sqrt{(-3)^2+4^2+(5-a)^2} & \quad \scriptsize \\[5pt] 5 &=&\sqrt{9+16+(5-a)^2} & \quad \scriptsize \\[5pt] 5 &=&\sqrt{25+(5-a)^2} \quad \scriptsize \mid ^2\\[5pt] 25 &=& 25+(5-a)^2 \quad \scriptsize \mid -25\\[5pt] 0 &=& (5-a)^2 & \quad \scriptsize \\[5pt] \end{array}$

Mit dem Satz des Nullprodukts folgt $a = 5.$

3.2

Damit ein rechter Winkel vorliegt, muss das Skalarprodukt der Ortsvektoren $0$ ergeben.

$\begin{array}[t]{rll} 0 &=& \overrightarrow{OB} \circ \overrightarrow{AB}& \quad \scriptsize \\[5pt] 0 &=& \pmatrix{2\\4\\5} \circ \pmatrix{-3\\4\\5-a} & \quad \scriptsize \\[5pt] 0 &=& 2\cdot(-3)+4\cdot4+5\cdot(5-a)& \quad \scriptsize \\[5pt] 0 &=& -6+16+25-5a& \quad \scriptsize \\[5pt] 0 &=& 35-5a \quad \scriptsize \mid +5a\\[5pt] 5a &=& 35 \qquad \scriptsize \mid :5\\[5pt] a &=& 7& \qquad \scriptsize \\[5pt] \end{array}$

4.1

Bei einem sechseitigen Würfel ist die Wahrscheinlichkeit $\dfrac{5}{6}$ , dass keine $6$ gewürfelt wird.
Wenn nun zweimal hintereinander gewürfelt wird, ist die Wahrscheinlichkeit (keine $6$ zu würfeln) $\dfrac{5}{6}\cdot\dfrac{5}{6}=\dfrac{25}{36}.$

4.2

Bei einem Histogramm für die Wahrscheinlichkeit, dass keine $6$ gewürfelt wird, müsste die höchste Säule bei $25$ sein. Rechts und links von der höchsten Säule nehmen die Säulen kontinuierlich ab. Da $36$ mal geworfen wird, kann es keine Wahrscheinlichkeiten bei Werten $\gt36$ geben. Alle Säulen ergeben in Summe $1$ .

Abbildung 1: Die höchste Säule ist bei $20$ , statt bei $25$ .
Abbildung 2: Die Summe aller Säulen ist $\gt1$ .
Abbildung 3: Die Säule bei $37$ ist $\neq 0$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?