2 Analysis
2.1
Gegeben sind die in  definierten Funktionen
definierten Funktionen  und
und  mit
mit  und
und 
Die Graphen von und
und  haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der
haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der  -Achse. Für die erste Ableitungsfunktion von
-Achse. Für die erste Ableitungsfunktion von  gilt
gilt 
Die Graphen von
2.1.1
Beschreibe, wie der Graph von  aus dem Graphen von
aus dem Graphen von  erzeugt werden kann. Gib die Wertemenge von
erzeugt werden kann. Gib die Wertemenge von  an.
an.
(2 BE)
2.1.2
Berechne die Größe des Winkels, in dem der Graph von  die Gerade mit der Gleichung
die Gerade mit der Gleichung  schneidet.
schneidet.
(3 BE)
2.1.3
Zeige, dass die Graphen von  und
und  in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
(3 BE)
2.1.4
Gib die geometrische Bedeutung der Gleichung  an und bestimme den Wert von
an und bestimme den Wert von 
(3 BE)
2.2
Für jeden Wert von  ist eine in
ist eine in  definierte Funktion
definierte Funktion  mit
mit  gegeben.
gegeben.
2.2.1
Berechne den Abstand der beiden Extrempunkte des Graphen von 
(4 BE)
2.2.2
Für jeden Wert von  mit
mit  hat der Graph von
hat der Graph von  zwei Extrempunkte.
zwei Extrempunkte.
Bestimme die -Koordinaten dieser beiden Extrempunkte in Abhängigkeit von
-Koordinaten dieser beiden Extrempunkte in Abhängigkeit von 
Begründe, dass es zu jeder Stelle einen Wert von
einen Wert von  gibt, für den der Graph von
gibt, für den der Graph von  im Punkt
im Punkt  einen Hochpunkt hat.
einen Hochpunkt hat.
Bestimme die
Begründe, dass es zu jeder Stelle
(5 BE)
2.3
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen.
Die in definierte Funktion
definierte Funktion  mit
mit  beschreibt für
beschreibt für  die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle. Dabei ist
die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle. Dabei ist  die seit Beobachtungsbeginn vergangene Zeit in Sekunden und
die seit Beobachtungsbeginn vergangene Zeit in Sekunden und  die momentane Durchflussrate in Kubikmetern pro Sekunde.
die momentane Durchflussrate in Kubikmetern pro Sekunde.
Die Abbildung zeigt den Graphen von
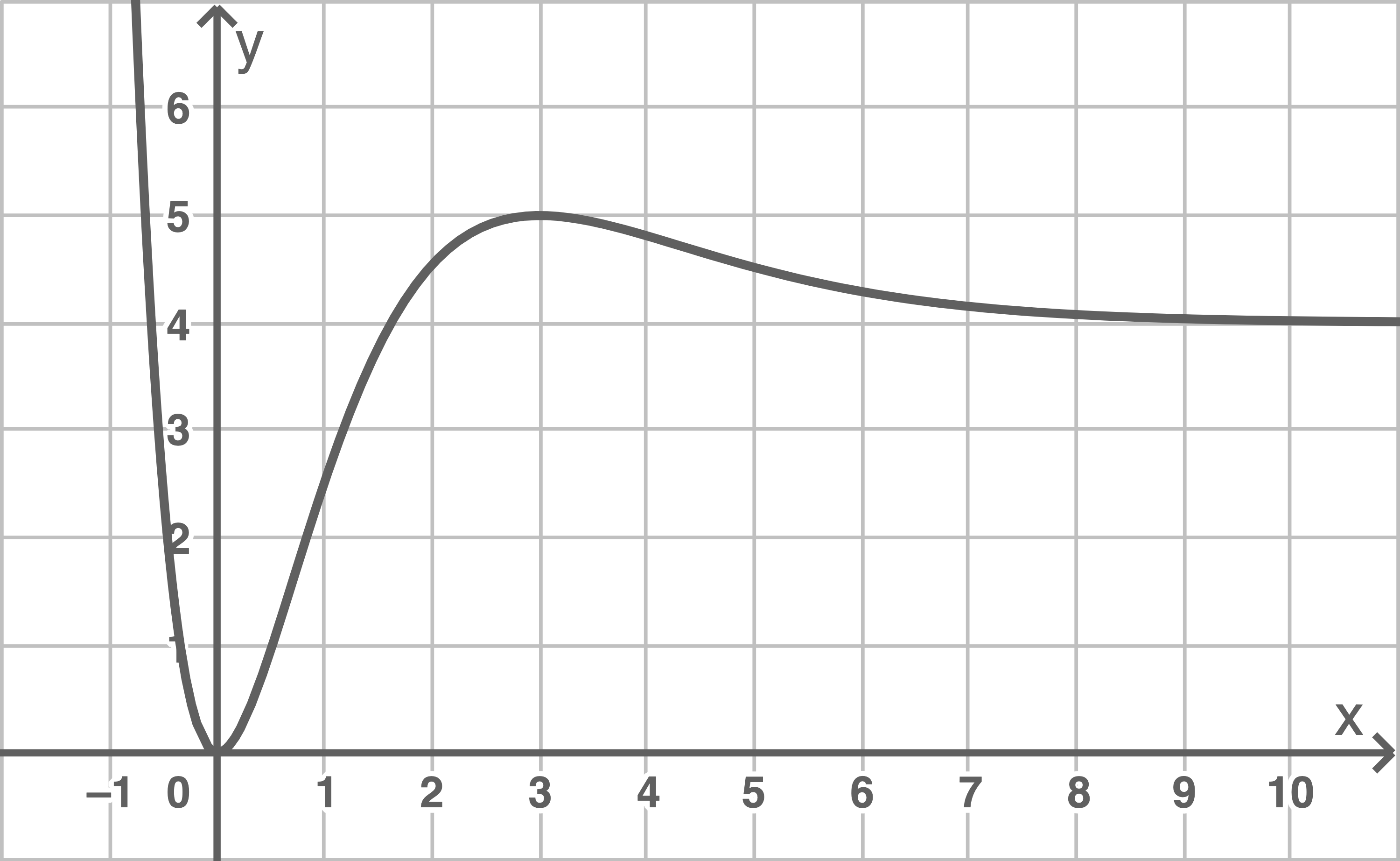
Die in
Die Abbildung zeigt den Graphen von

2.3.1
Gib den Wert des Terms  sowie die Bedeutung dieses Werts im Sachzusammenhang an.
sowie die Bedeutung dieses Werts im Sachzusammenhang an.
(2 BE)
2.3.2
Bestimme die momentane Durchflussrate für denjenigen Zeitpunkt, zu dem sie am stärksten abnimmt.
(3 BE)
2.3.3
Betrachtet wird der Zeitraum der ersten zehn Sekunden nach Beobachtungsbeginn.
Beschreibe unter Verwendung geeigneter Flächen die graphische Bedeutung der folgenden Aussage: Für den betrachteten Zeitraum beträgt die mittlere Durchflussrate etwa .
.
Beschreibe unter Verwendung geeigneter Flächen die graphische Bedeutung der folgenden Aussage: Für den betrachteten Zeitraum beträgt die mittlere Durchflussrate etwa
(3 BE)
2.3.4
Die Tangente an den Graphen von  im Punkt
im Punkt  wird durch die Gleichung
wird durch die Gleichung  dargestellt.
dargestellt.
Interpretiere die folgende Aussage im Sachzusammenhang: Für alle Werte von![\(x \in[0,7 ; 1,4]\)](https://mathjax.schullv.de/33433d08b4b8e623af15cb856a50b067fabd9869023da6aadb4d6566d6f30339?color=5a5a5a) gilt
gilt 
Interpretiere die folgende Aussage im Sachzusammenhang: Für alle Werte von
(3 BE)
2.3.5
An der Messstelle fließen in einem Zeitraum von drei Sekunden dreizehn Kubikmeter Wasser vorbei.
Berechne die dafür infrage kommenden Zeiträume.
Berechne die dafür infrage kommenden Zeiträume.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1.1
Der Graph von  wird an der
wird an der  -Achse gespiegelt.
Wertemenge:
-Achse gespiegelt.
Wertemenge: ![\(\left] - \infty; 0 \right[\)](https://mathjax.schullv.de/f40cd97f45db574f2ffce3a2e62c2c71203f6c1275fd4ec7c73600a9f6800ed9?color=5a5a5a)
2.1.2
1. Schritt: Schnittstelle berechnen
![\(\begin{array}[t]{rll}
q(x) &=& 4 \\[5pt]
\mathrm e^{-x} &=& 4 &\quad \scriptsize \mid\;\ln \\[5pt]
-x &=& \ln 4 &\quad \scriptsize \mid\;\cdot (-1)\\[5pt]
x &=& -\ln 4
\end{array}\)](https://mathjax.schullv.de/69c2d84949f43db8053400ac59414766158be53c59f8752bac58eeda0bac761a?color=5a5a5a) 2. Schritt: Schnittwinkel berechnen
Da die Gerade mit der Gleichung
2. Schritt: Schnittwinkel berechnen
Da die Gerade mit der Gleichung  parallel zur
parallel zur  -Achse verläuft, entspricht der Schnittwinkel des Graphen von
-Achse verläuft, entspricht der Schnittwinkel des Graphen von  mit der Geraden dem Steigungswinkel des Graphen von
mit der Geraden dem Steigungswinkel des Graphen von  in der Schnittstelle.
in der Schnittstelle.

 Mit der Formel für den Steigungswinkel
Mit der Formel für den Steigungswinkel  folgt:
folgt:
![\(\begin{array}[t]{rll}
\tan \alpha &=& q](https://mathjax.schullv.de/d7e7fbec83c3a63ad03e59f4808cb955bac8773575ce92197fe90b9f2f7e4c90?color=5a5a5a) Der Winkel, unter dem der Graph von
Der Winkel, unter dem der Graph von  die Gerade mit der Gleichung
die Gerade mit der Gleichung  schneidet, ist ca.
schneidet, ist ca.  groß.
groß.
2.1.3
In der Aufgabenstellung ist angegeben, dass sich der gemeinsame Punkt auf der  -Achse befindet. Für ihn gilt also
-Achse befindet. Für ihn gilt also  Damit die beiden Graphen an dieser Stelle eine gemeinsame Tangente haben, muss ebenfalls die Steigung übereinstimmen:
Damit die beiden Graphen an dieser Stelle eine gemeinsame Tangente haben, muss ebenfalls die Steigung übereinstimmen:

 Es gilt also
Es gilt also  und
und  An der Stelle
An der Stelle  haben die Graphen von
haben die Graphen von  und
und  daher eine gemeinsame Tangente mit der Gleichung:
daher eine gemeinsame Tangente mit der Gleichung:

2.1.4
Der Integrand ist die Differenzfunktion aus  und
und  Das bestimmte Integral liefert also den Flächeninhalt zwischen beiden Funktionsgraphen.
Das bestimmte Integral liefert also den Flächeninhalt zwischen beiden Funktionsgraphen.
Betrachtet wird die Fläche zwischen den Graphen von und
und  sowie einer zur
sowie einer zur  -Achse parallelen Geraden
-Achse parallelen Geraden  mit dem Inhalt
mit dem Inhalt  Das Lösen dieser Gleichung mit dem CAS liefert
Das Lösen dieser Gleichung mit dem CAS liefert 
Betrachtet wird die Fläche zwischen den Graphen von
2.2.1
Mit dem CAS können die Stellen bestimmt werden, an denen das notwendige Kriterium für Extremstellen erfüllt ist. Dafür kann auch die erste Ableitungsfunktion mit dem CAS bestimmt werden.
![\(\begin{array}[t]{rll}
h_1](https://mathjax.schullv.de/dc833dbe8d149fd2bd4f49734a2f00be74afb3a1b80e308074a0b9a60d2741b0?color=5a5a5a) Da in der Aufgabenstellung angegeben ist, dass es genau zwei Extrempunkte gibt, kann auf die Überprüfung des hinreichenden Kriteriums verzichtet werden.
Da in der Aufgabenstellung angegeben ist, dass es genau zwei Extrempunkte gibt, kann auf die Überprüfung des hinreichenden Kriteriums verzichtet werden.



2.2.2
Extremstellen bestimmen
Mit dem CAS können die Stellen bestimmt werden, an denen das notwendige Kriterium für Extremstellen erfüllt ist. Dafür kann auch die erste Ableitungsfunktion mit dem CAS bestimmt werden.
![\(\begin{array}[t]{rll}
h_a](https://mathjax.schullv.de/0368069871fc5856773ad74f832c25003c01d3c9752a28c8b8a6405b30afb302?color=5a5a5a) Hochpunkt begründen
Für
Hochpunkt begründen
Für  gilt:
gilt:  da
da  Für
Für  ist der Ausdruck unter der Wurzel größer als
ist der Ausdruck unter der Wurzel größer als  somit gibt es dann zwei Extremstellen.
somit gibt es dann zwei Extremstellen.
 Somit ist
Somit ist  die kleinste Lösung für
die kleinste Lösung für 
Wird größer, so wird auch
größer, so wird auch  größer. Also gibt es für jede Stelle
größer. Also gibt es für jede Stelle  einen zugehörigen Graphen von
einen zugehörigen Graphen von  der an der Stelle
der an der Stelle  einen Extrempunkt hat.
einen Extrempunkt hat.
Für alle Werte von ist
ist  somit sind die Extrempunkte an der Stelle
somit sind die Extrempunkte an der Stelle  Hochpunkte.
Hochpunkte.
Wird
Für alle Werte von
2.3.1
Der Graph von  besitzt eine waagerechte Asymptote mit der Gleichung
besitzt eine waagerechte Asymptote mit der Gleichung  Somit ist:
Somit ist:
 Langfristig nähert sich die momentane Durchflussrate dem Wert
Langfristig nähert sich die momentane Durchflussrate dem Wert  an.
an.
2.3.2
Der gesuchte Zeitpunkt ist dadurch gekennzeichnet, dass der Graph den kleinsten Anstieg besitzt. Dies ist näherungsweise bei  der Fall.
der Fall.
Die zugehörige momentane Änderungsrate entspricht dem Funktionswert an dieser Stelle und beträgt rund Alternativ
Die stärkste Abnahme der momentanen Durchflussrate liegt an dem Zeitpunkt vor, der der Wendestelle mit negativen Anstieg entspricht:
Alternativ
Die stärkste Abnahme der momentanen Durchflussrate liegt an dem Zeitpunkt vor, der der Wendestelle mit negativen Anstieg entspricht:
 gilt für
gilt für  und
und 

 Der gesuchte Zeitpunkt ist somit
Der gesuchte Zeitpunkt ist somit  Sekunden nach Beginn. Die momentane Änderungsrate beträgt
Sekunden nach Beginn. Die momentane Änderungsrate beträgt  .
.
Die zugehörige momentane Änderungsrate entspricht dem Funktionswert an dieser Stelle und beträgt rund
2.3.3
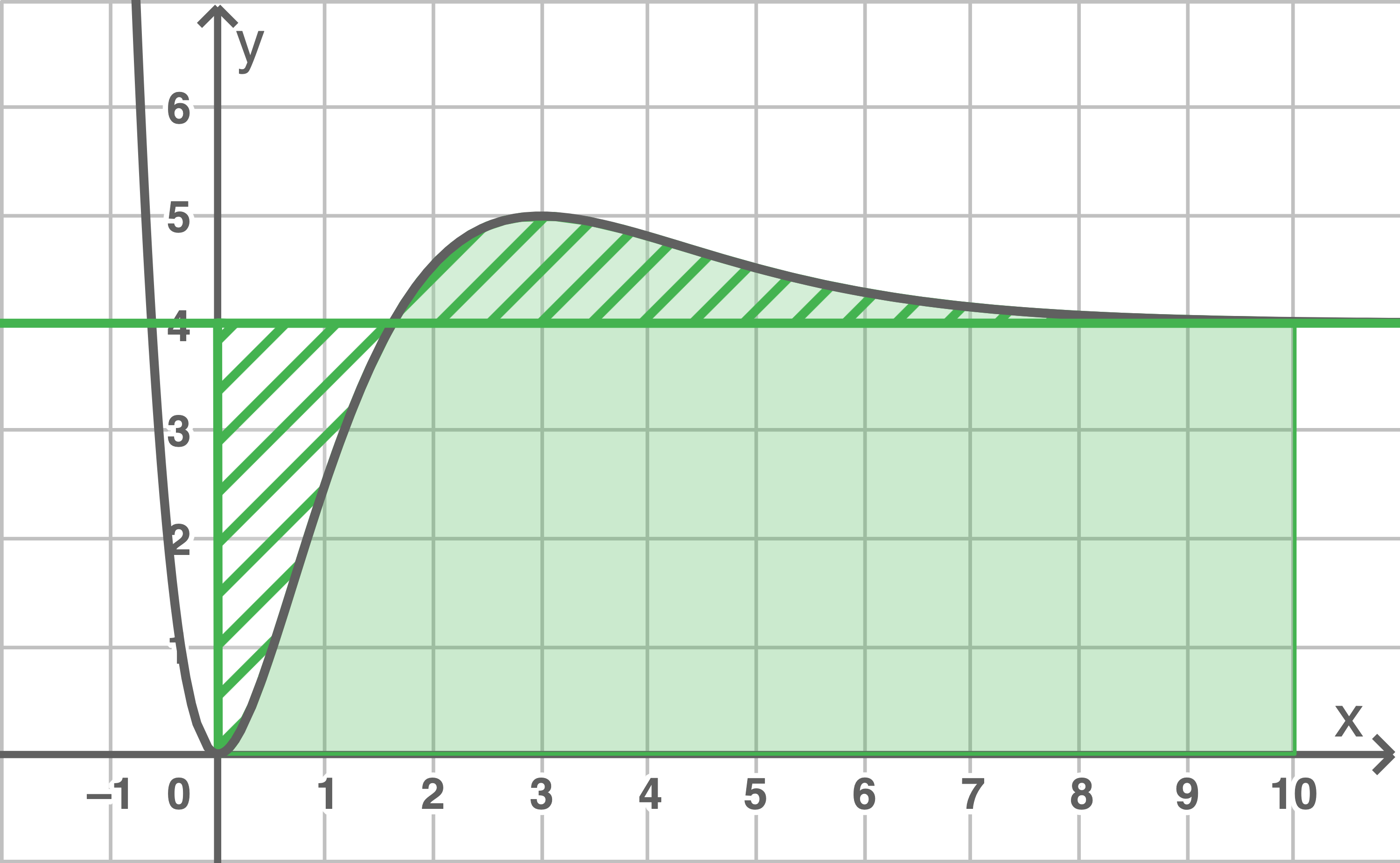
Die mittlere Durchflussrate von
2.3.4
Im Zeitraum von  Sekunden nach Beobachtungsbeginn bis
Sekunden nach Beobachtungsbeginn bis  Sekunden nach Beobachtungsbeginn beschreibt die Tangente die zeitliche Entwicklung der momentanen Durchflussrate mit einer maximalen relativen Abweichung von
Sekunden nach Beobachtungsbeginn beschreibt die Tangente die zeitliche Entwicklung der momentanen Durchflussrate mit einer maximalen relativen Abweichung von 
2.3.5
Für den rekonstruierten Bestand von  in einem Zeitraum von
in einem Zeitraum von  Sekunden gilt:
Sekunden gilt:
 Mit dem CAS folgen die Lösungen:
Mit dem CAS folgen die Lösungen:

 und
und  Die erste Lösung entfällt, da
Die erste Lösung entfällt, da  Die gesuchten Zeiträume sind somit
Die gesuchten Zeiträume sind somit  bis
bis  sowie
sowie  bis
bis 