Analysis
1.
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  .
.
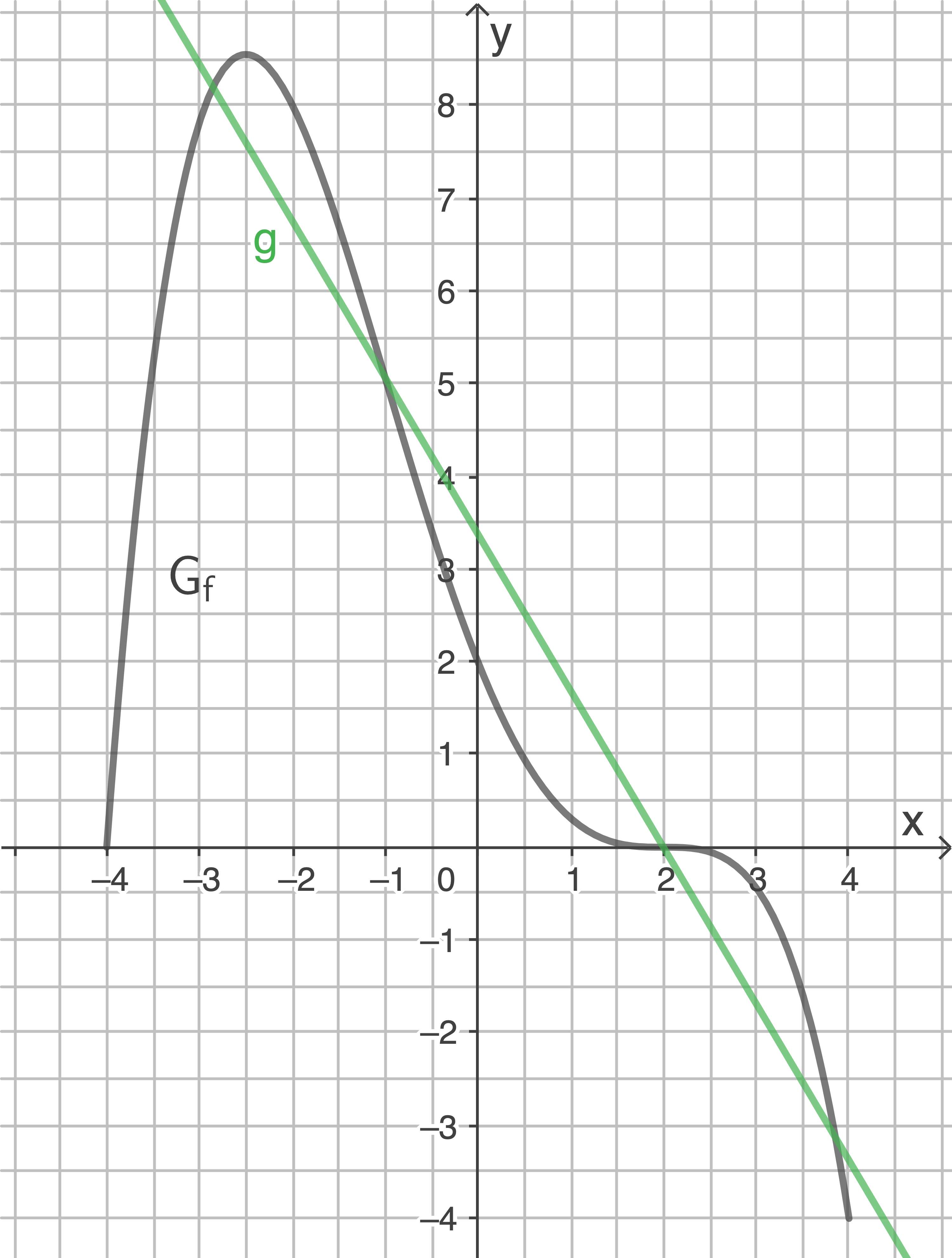
Der Graph von wird mit
wird mit  bezeichnet.
bezeichnet.
Der Graph von
1.1
Gib die Koordinaten der Schnittpunkte von  mit den Koordinatenachsen an.
mit den Koordinatenachsen an.
(2 BE)
1.2
Begründe ohne weitere Rechnung, dass  mindestens einen Hochpunkt hat.
mindestens einen Hochpunkt hat.
(3 BE)
1.3
Weise rechnerisch nach, dass auch
(3 BE)
1.4
Die Gerade  verläuft durch
verläuft durch  und
und  .
.
1.4.1
Stelle  für
für  in einem Koordinatensystem dar.
in einem Koordinatensystem dar.
Zeichne in dieses Koordinatensystem ein und weise nach, dass
in dieses Koordinatensystem ein und weise nach, dass  durch die Gleichung
durch die Gleichung  dargestellt wird.
dargestellt wird.
Zeichne
(4 BE)
1.4.2
(4 BE)
1.4.3
Ermittle rechnerisch die Anzahl der Geraden, die parallel zu  sind und
sind und  berühren.
berühren.
(3 BE)
1.5
Im Längsschnitt eines Berghangs kann dessen Profillinie für  modellhaft durch den Graphen der in
modellhaft durch den Graphen der in  definierten Funktion
definierten Funktion  mit
mit  , d.h.
, d.h.  , beschrieben werden.
, beschrieben werden.
Es soll davon ausgegangen werden, dass der Hang in Querrichtung nicht geneigt ist. Im verwendeten Koordinatensystem beschreibt die -Achse die Horizontale; eine Längeneinheit entspricht 100 Metern in der Wirklichkeit.
-Achse die Horizontale; eine Längeneinheit entspricht 100 Metern in der Wirklichkeit.
Es soll davon ausgegangen werden, dass der Hang in Querrichtung nicht geneigt ist. Im verwendeten Koordinatensystem beschreibt die
1.5.1
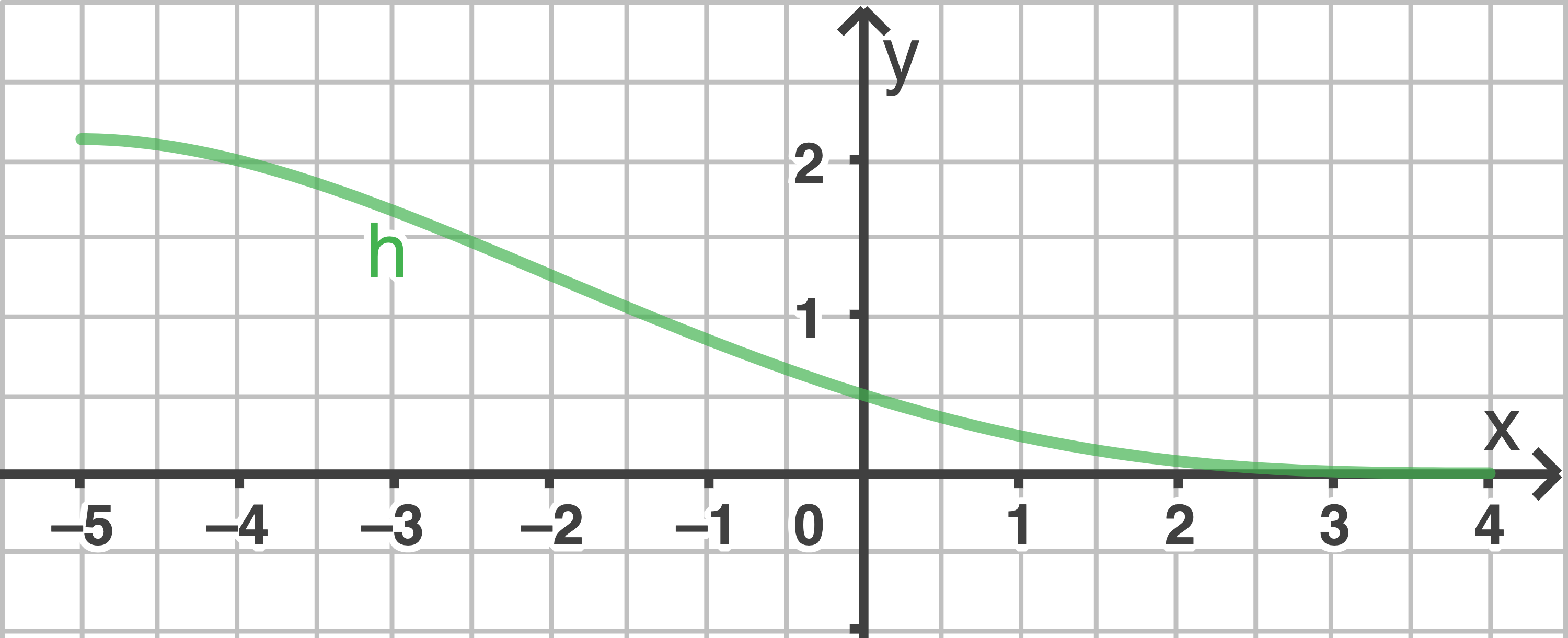
Der Hochpunkt des Graphen von  hat die
hat die  -Koordinate -5.
-Koordinate -5.
Gib die zugehörige -Koordinate an und stelle die Profillinie des Hangs in einem Koordinatensystem grafisch dar.
-Koordinate an und stelle die Profillinie des Hangs in einem Koordinatensystem grafisch dar.
Gib die zugehörige
(2 BE)
1.5.2
Beschreibe, wie der Graph von  aus dem Graphen von
aus dem Graphen von  erzeugt werden kann.
erzeugt werden kann.
(2 BE)
1.5.3
Zeige rechnerisch, dass der Höhenunterschied zwischen dem höchsten und tiefsten Punkt des Hangs etwa 214 beträgt.
beträgt.
Ermittle das durchschnittliche Gefälle zwischen diesen beiden Punkten in Prozent.
Ermittle das durchschnittliche Gefälle zwischen diesen beiden Punkten in Prozent.
(4 BE)
1.5.4
Der Hang wird als Skipiste genutzt. Der Tabelle kann der Zusammenhang zwischen dem Schwierigkeitsgrad von Skipisten und deren jeweiligem maximalen Gefälle entnommen werden:
Ermittle den Schwierigkeitsgrad der hier betrachteten Piste.
| Schwierigkeitsgrad | maximales Gefälle |
|---|---|
| leicht | bis 25 % |
| mittel | bis 40 % |
| schwer | mehr als 40 % |
Ermittle den Schwierigkeitsgrad der hier betrachteten Piste.
(3 BE)
1.5.5
Am höchsten Punkt des Hangs steht ein Turm mit einer Höhe von 25 . Es gibt zwei Abschnitte des Hangs, in denen der Turm vom Boden aus zumindest teilweise sichtbar ist.
. Es gibt zwei Abschnitte des Hangs, in denen der Turm vom Boden aus zumindest teilweise sichtbar ist.
Ermittle die Lage des höher gelegenen der beiden Abschnitte.
Ermittle die Lage des höher gelegenen der beiden Abschnitte.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Mit dem CAS lassen sich die Schnittpunkte mit den Achsen bestimmen.
Schnittpunkte mit der x-Achse
Mit dem Solve-Befehl des CAS ( nach
nach  lösen) lassen sich die Schnittstellen mit der x-Achse bestimmen. Damit folgen die Schnittpunkte
lösen) lassen sich die Schnittstellen mit der x-Achse bestimmen. Damit folgen die Schnittpunkte  und
und  Schnittpunkt mit der y-Achse
Schnittpunkt mit der y-Achse
Aus folgt der Schnittpunkt
folgt der Schnittpunkt  mit der y-Achse.
mit der y-Achse.
Mit dem Solve-Befehl des CAS (
Aus
1.2
Die Funktion  ist eine ganzrationale Funktion. Aus Aufgbabenteil
ist eine ganzrationale Funktion. Aus Aufgbabenteil  ist bekannt, welche Nullstellen die Funktion hat. Es gilt
ist bekannt, welche Nullstellen die Funktion hat. Es gilt  und
und  . Daraus folgt, dass
. Daraus folgt, dass  mindestens einen Hochpunkt für
mindestens einen Hochpunkt für  hat.
hat.
1.3
1. Schritt: Erste und zweite Ableitung bilden
Mit dem CAS lassen sich die Ableitungen wie folgt bestimmen:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II

 2. Schritt: Notwendige Bedingung für Wendestellen
2. Schritt: Notwendige Bedingung für Wendestellen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/e8cff294da39f00e1f6c55fdd08038be133d6770f1aa404f585cbffbd7f8a911?color=5a5a5a) Mit dem Satz des Nullprodukts folgt
Mit dem Satz des Nullprodukts folgt  und daraus
und daraus  oder
oder  und daraus
und daraus  Es gibt also maximal zwei Wendepunkte. Aus den x-Koordinaten und dem gegebenen Wendepunkt folgt, dass sich
Es gibt also maximal zwei Wendepunkte. Aus den x-Koordinaten und dem gegebenen Wendepunkt folgt, dass sich  an der Stelle
an der Stelle  befinden muss.
3. Schritt: Hinreichende Bedingung überprüfen
befinden muss.
3. Schritt: Hinreichende Bedingung überprüfen
 4. Schritt: Einsetzen in die Funktion
4. Schritt: Einsetzen in die Funktion
 Damit ist
Damit ist  ein Wendepunkt.
ein Wendepunkt.
Mit dem CAS lassen sich die Ableitungen wie folgt bestimmen:
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

1.4
1.4.1
Um zu zeigen, dass  durch die Gleichung
durch die Gleichung  beschrieben werden kann, reicht es zu überprüfen, ob die x- und y-Koordinaten von
beschrieben werden kann, reicht es zu überprüfen, ob die x- und y-Koordinaten von  und
und  die Gleichung erfüllen.
x-Koordinate von
die Gleichung erfüllen.
x-Koordinate von  einsetzen
einsetzen
 Das Ergebnis entspricht der y-Koordinate von
Das Ergebnis entspricht der y-Koordinate von  .
x-Koordinate von
.
x-Koordinate von  einsetzen
einsetzen
 Das Ergebnis entspricht der y-Koordinate von
Das Ergebnis entspricht der y-Koordinate von  Damit erfüllen die x- und y-Koordinaten von
Damit erfüllen die x- und y-Koordinaten von  und
und  die gegebene Gleichung und
die gegebene Gleichung und  kann durch diese beschrieben werden.
kann durch diese beschrieben werden.
1.4.2
1. Schritt: Schnittstellen von Graph von  und
und  bestimmen
bestimmen
Durch Gleichsetzen von und
und  lassen sich die Schnittstellen ermitteln.
lassen sich die Schnittstellen ermitteln.
![\(\begin{array}[t]{rll}
f(x) &=& -\dfrac{27}{16}x+\dfrac{27}{8} \\[5pt]
\left(2+\dfrac{x}{2}\right)\cdot\left(1-\dfrac{x}{2}\right)^3 &=& -\dfrac{27}{16}x+\dfrac{27}{8} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/bf33c074536b4ddb4d881b57b5e1244873e6f870013a661a061f7a6d7cb90442?color=5a5a5a) Mit dem Solve-Befehl des CAS folgt:
Mit dem Solve-Befehl des CAS folgt:



 2. Schritt: Integral berechnen
2. Schritt: Integral berechnen
Mit dem CAS kann der Wert des folgenden Integrals berechnet werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 Da das Integral Null ergibt, muss der Inhalt einer der drei Flächen, welche von
Da das Integral Null ergibt, muss der Inhalt einer der drei Flächen, welche von  und dem Graphen von
und dem Graphen von  eingeschlossen werden, genau dem Inhalt der beiden anderen Flächen entsprechen.
eingeschlossen werden, genau dem Inhalt der beiden anderen Flächen entsprechen.
Durch Gleichsetzen von
Mit dem CAS kann der Wert des folgenden Integrals berechnet werden.
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

1.4.3
Geraden, die  berühren sind Tangenten. Damit diese parallel zur Gerade
berühren sind Tangenten. Damit diese parallel zur Gerade  sind, müssen sie dieselbe Steigung wie
sind, müssen sie dieselbe Steigung wie  besitzen.
1. Schritt:
besitzen.
1. Schritt:  -Koordinaten bestimmen, an denen
-Koordinaten bestimmen, an denen  dieselbe Steigung besitzt, wie der Graph von
dieselbe Steigung besitzt, wie der Graph von 
Mit dem CAS lässt sich die erste Ableitung von berechnen.
berechnen.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 Nun gilt es die Stellen zu bestimmen, an denen
Nun gilt es die Stellen zu bestimmen, an denen  die Steigung
die Steigung  annimmt.
annimmt.
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/0eddf67f2eaa2f1c2f098b3a24a63b3bb4299e9e8cea046c33f03502ee2cf365?color=5a5a5a) Mit dem Solve-Befehl des CAS lassen sich folgende Stellen berechnen:
Mit dem Solve-Befehl des CAS lassen sich folgende Stellen berechnen: 
 und
und  Da es möglich ist, dass eine Tangente den Graphen an zwei dieser Stellen berührt, müssen die Tangenten explizit bestimmt werden.
2. Schritt: Berechnung der Tangenten
Da es möglich ist, dass eine Tangente den Graphen an zwei dieser Stellen berührt, müssen die Tangenten explizit bestimmt werden.
2. Schritt: Berechnung der Tangenten
Mit dem dem tanLine-Befehl (CASIO ClassPad) bzw. tangentLine-Befehl (TI-Inspire) lassen sich die Tangenten an den jeweiligen Stellen bestimmen. 2.1 Schritt: Tangente an der Stelle Die Tangentengleichung lautet
Die Tangentengleichung lautet  2.2 Schritt: Tangente an der Stelle
2.2 Schritt: Tangente an der Stelle  Die Tangentengleichung lautet
Die Tangentengleichung lautet  2.3 Schritt: Tangente an der Stelle
2.3 Schritt: Tangente an der Stelle  Die Tangentengleichung lautet
Die Tangentengleichung lautet  Es gibt damit genau zwei Geraden, welche parallel zu
Es gibt damit genau zwei Geraden, welche parallel zu  sind und
sind und  berühren.
berühren.
Mit dem CAS lässt sich die erste Ableitung von
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

Mit dem dem tanLine-Befehl (CASIO ClassPad) bzw. tangentLine-Befehl (TI-Inspire) lassen sich die Tangenten an den jeweiligen Stellen bestimmen. 2.1 Schritt: Tangente an der Stelle
1.5.1
1. Schritt:  -Koordinate angeben
-Koordinate angeben

 Damit ist die
Damit ist die  -Koordinate
-Koordinate  .
2. Schritt: Profillinie grafisch darstellen
.
2. Schritt: Profillinie grafisch darstellen
1.5.2
Um den Graphen  zu erzeugen wird
zu erzeugen wird  um den Faktor
um den Faktor  in
in  -Richtung und um den Faktor
-Richtung und um den Faktor  in
in  -Richtung gestreckt.
-Richtung gestreckt.
1.5.3
1. Schritt: Tiefste Stelle ermitteln
Der höchste Punkt ist bereits in Aufgaben in Form des Hochpunktes gegeben. Nun müssen noch die Koordinaten des tiefsten Punktes bestimmt werden.
Mit Hilfe des CAS lassen sich die beiden Ableitungen bestimmen.
in Form des Hochpunktes gegeben. Nun müssen noch die Koordinaten des tiefsten Punktes bestimmt werden.
Mit Hilfe des CAS lassen sich die beiden Ableitungen bestimmen.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Die Ableitungen sind:
Casio Classpad II
Die Ableitungen sind:

 Mit der notwendigen Bedingung für Extremstellen folgt:
Mit der notwendigen Bedingung für Extremstellen folgt:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/a4edc924524393cbe2f318131388ad39d5a316dd20da918c074608617a48a694?color=5a5a5a) Mit dem Satz des Nullprodukts folgt
Mit dem Satz des Nullprodukts folgt  und
und  Auf die Überprüfung der hinreichenden Bedingung kann verzichtet werden, da
Auf die Überprüfung der hinreichenden Bedingung kann verzichtet werden, da  und
und  auf den Rändern des Intervalls liegen. Somit muss die tiefste Stelle auch auf einem Rand des Intervalls liegen. Bei
auf den Rändern des Intervalls liegen. Somit muss die tiefste Stelle auch auf einem Rand des Intervalls liegen. Bei  liegt ein Maximum und somit die höchste Stelle vor. Demnach muss bei
liegt ein Maximum und somit die höchste Stelle vor. Demnach muss bei  die tiefste Stelle vorliegen.
2. Schritt: Höhenunterschied bestimmen
die tiefste Stelle vorliegen.
2. Schritt: Höhenunterschied bestimmen
Der Höhenunterschied zwischen dem höchsten und dem tiefsten Punkt ist: 3. Schritt: Gefälle zwischen den beiden Punkten ermitteln
Um das Gefälle zu bestimmen, wird das Steigungsdreieck gebildet. Das Gefälle beträgt damit etwa
Das Gefälle beträgt damit etwa 
Der höchste Punkt ist bereits in Aufgaben
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

Der Höhenunterschied zwischen dem höchsten und dem tiefsten Punkt ist: 3. Schritt: Gefälle zwischen den beiden Punkten ermitteln
Um das Gefälle zu bestimmen, wird das Steigungsdreieck gebildet.
1.5.4
Die Stelle, an der das Gefälle maximal ist, entspricht gerade der Stelle, an der die Steigung von  minimal ist. Mit dem CAS lässt sich das tiefste Punkt von
minimal ist. Mit dem CAS lässt sich das tiefste Punkt von  im gegebenen Intervall bestimmen.
im gegebenen Intervall bestimmen.
 TI nspire CAS
TI nspire CAS

 Der zugehörige Funktionswert lässt sich ebenfalls mit dem CAS berechnen:
Der zugehörige Funktionswert lässt sich ebenfalls mit dem CAS berechnen:
![\(\begin{array}[t]{lll}
h](https://mathjax.schullv.de/21ade2b06be88c9973644bc15e198e414b3e1c8cba7b18be595d93e3849fe7bf?color=5a5a5a)
 Casio Classpad II
Casio Classpad II

![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/d618fa1337c2f1e9c8757e35d7be49b369be3b149ae3138153315de0d6c7e150?color=5a5a5a) Da das maximale Gefälle etwa
Da das maximale Gefälle etwa  beträgt handelt es sich um eine schwere Piste.
beträgt handelt es sich um eine schwere Piste.
1.5.5
Da der  hohe Turm an der höchsten Stelle des Hangs steht, lauten die Koordinaten der Spitze
hohe Turm an der höchsten Stelle des Hangs steht, lauten die Koordinaten der Spitze  Die Abbildung zeigt die Spitze
Die Abbildung zeigt die Spitze  , den Graphen von
, den Graphen von  und die Sichtlinie
und die Sichtlinie  welche durch
welche durch  verläuft.
verläuft.
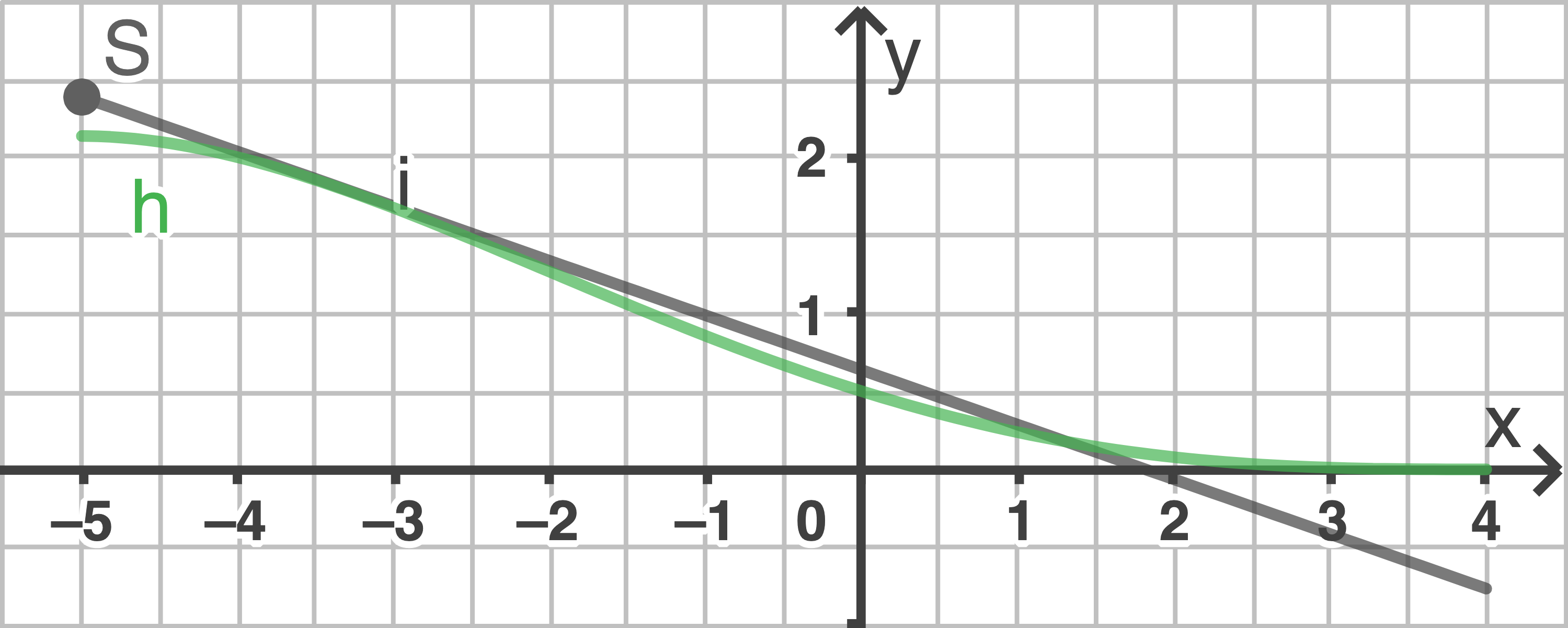 Es liegt nahe, dass das gesuchte Intervall bei
Es liegt nahe, dass das gesuchte Intervall bei  beginnt. Die rechte Grenze
beginnt. Die rechte Grenze  ist dann die Stelle, an der die Spitze des Turms gerade noch so zu sehen ist. Das ist genau dann der Fall, wenn
ist dann die Stelle, an der die Spitze des Turms gerade noch so zu sehen ist. Das ist genau dann der Fall, wenn  zum ersten Mal eine Tangente von
zum ersten Mal eine Tangente von  beschreibt. Für
beschreibt. Für  gilt:
gilt:
 Durch Einsetzen der Koordianten von
Durch Einsetzen der Koordianten von  lässt sich
lässt sich  berechnen.
Damit folgt für
berechnen.
Damit folgt für 


 Ist nun
Ist nun  eine Tangente von
eine Tangente von  muss gelten:
Mit dem CAS lässt sich das Gleichungssystem wie folgt lösen:
muss gelten:
Mit dem CAS lässt sich das Gleichungssystem wie folgt lösen:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Die kleinste Lösung im Intervall
Casio Classpad II
Die kleinste Lösung im Intervall ![\([-5,4]\)](https://mathjax.schullv.de/bfacabd1ffab8cd8b58e073e9652d0945eb6e8272bbe8b4d34c506e797de9e7a?color=5a5a5a) lautet:
lautet:  .
.
Damit ist der gesuchte Abschnitt, in dem der Turm zumindest teilweise sichtbar ist, .
.

menu  3: Algebra
3: Algebra  7
7
keyboard  Math1
Math1 

Damit ist der gesuchte Abschnitt, in dem der Turm zumindest teilweise sichtbar ist,