Pflichtteil A0
Analysis
1.
Gegeben ist die in 
definierte Funktion 
mit der Gleichung 
1.1
Gib die Nullstellen der Funktion an.
(2 BE)
1.2
Weise nach, dass der Koordinatenursprung der lokale Hochpunkt des Graphen der Funktion ist.
(3 BE)
1.3
Gib eine Gleichung einer ganzrationalen Funktion 
dritten Grades mit folgenden Eigenschaften an:
- Die Funktionen
- Der Punkt
ist Hochpunkt der Funktion
(1 BE)
2.
Es werden Funktionen mit der Definitionsmenge untersucht, für deren Ableitungsfunktionen folgende Gleichung gilt: 
2.1
Der Graph einer solchen Funktion besitzt an einer Stelle den Anstieg 
Bestimme den Funktionswert an dieser Stelle.
Bestimme den Funktionswert an dieser Stelle.
(2 BE)
2.2
Zeige, dass es auch eine konstante Funktion gibt, die diese Gleichung erfüllt.
(2 BE)
Analytische Geometrie
3.
Betrachte die Pyramide 
Ihre Grundfläche ist das rechtwinklige Dreieck 
die Hypotenuse 
ist 
lang, die Kathete 
Die Kante 
steht senkrecht zur Grundfläche und hat eine Länge von 
3.1
Berechne das Volumen der Pyramide.
(3 BE)
3.2
Die Pyramide soll in einem Koordinatensystem dargestellt werden, in dem eine Längeneinheit 
entspricht. Gib mögliche Koordinaten der Eckpunkte der Pyramide an.
(2 BE)
Stochastik
4.
Gegeben ist eine Zufallsvariable 
, welche nur die Werte 
und 
annimmt.
Für die Wahrscheinlichkeitsverteilung von gilt 
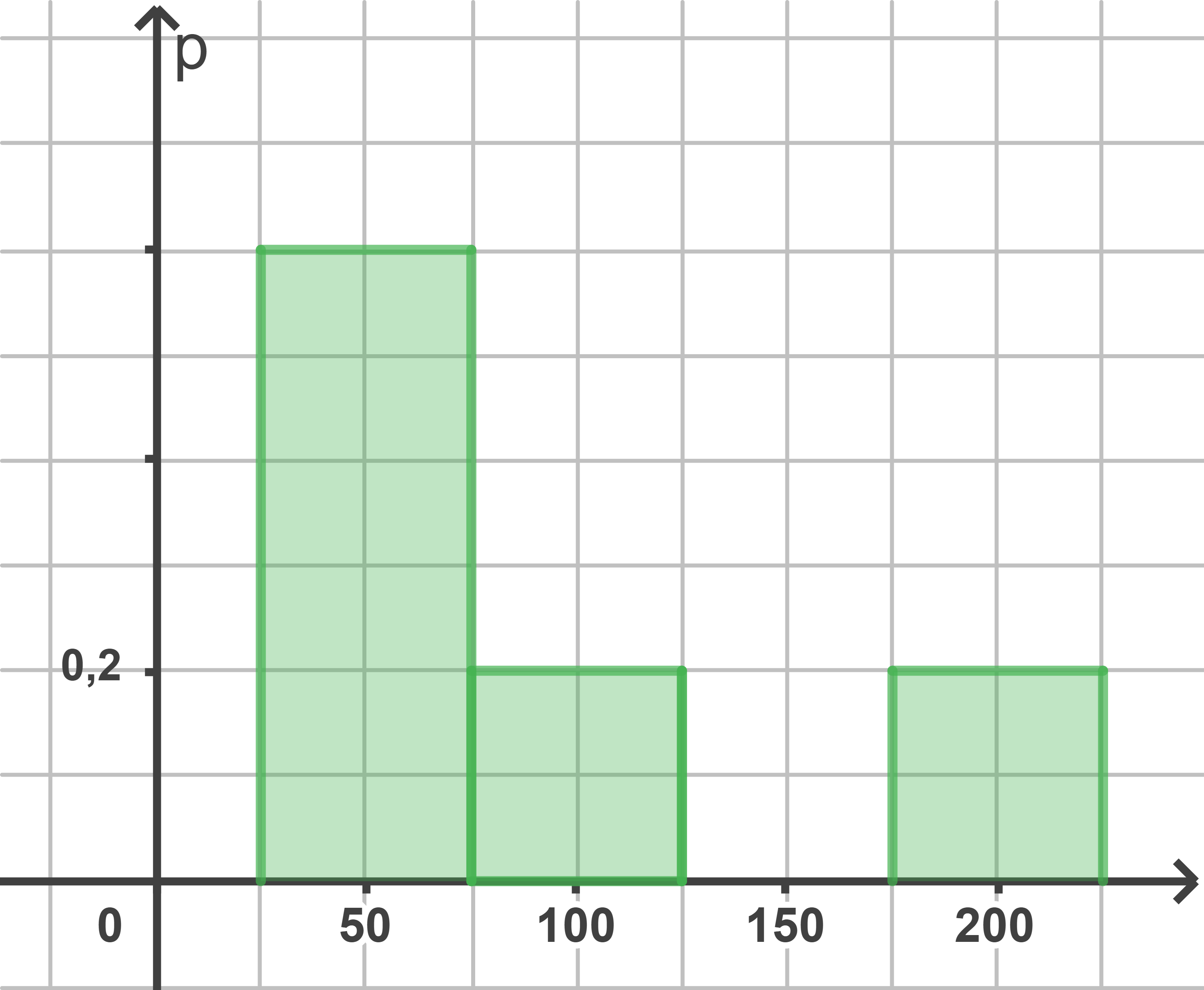
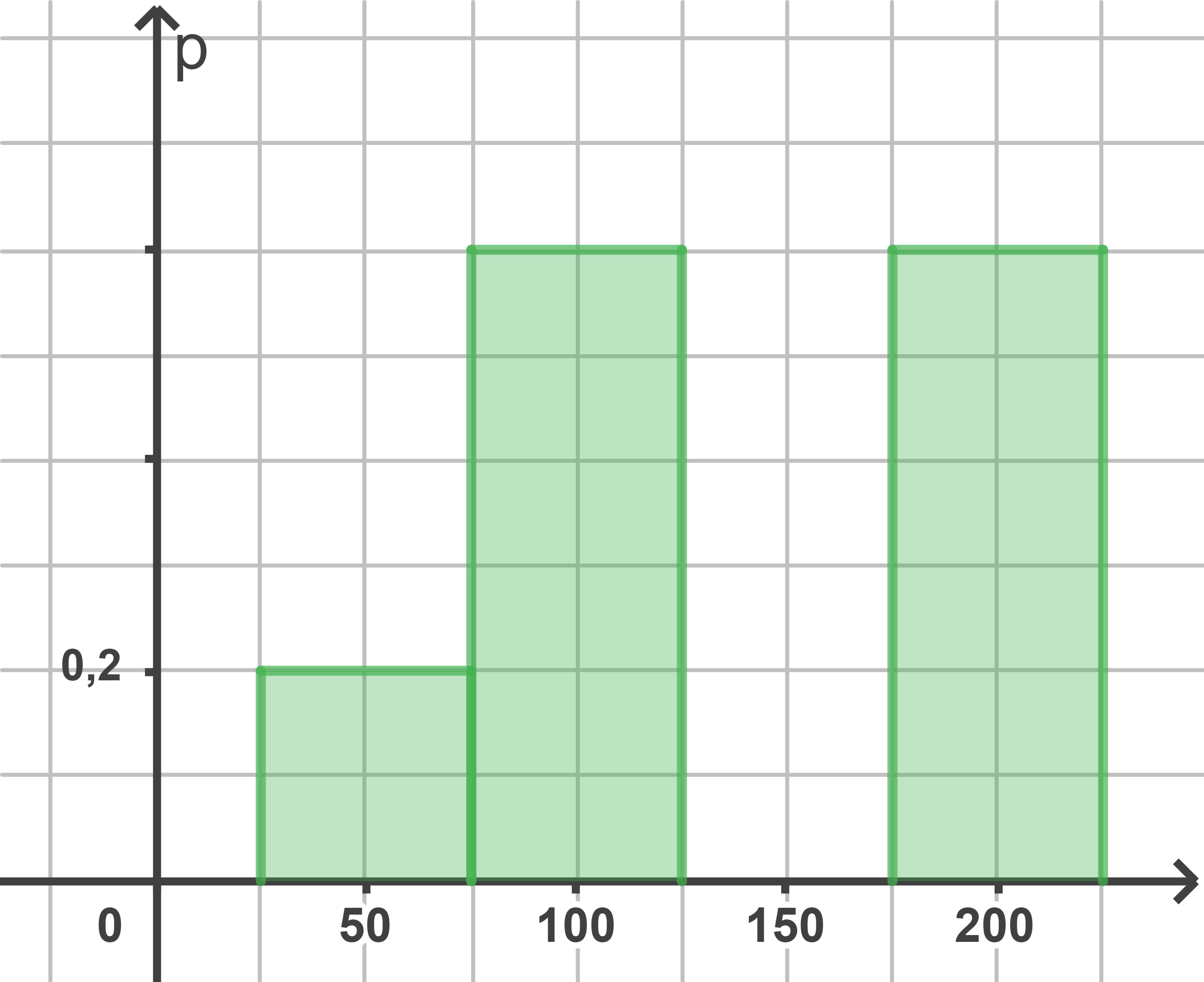
Eine der folgenden Abbildungen stellt diese Wahrscheinlichkeitsverteilung dar.
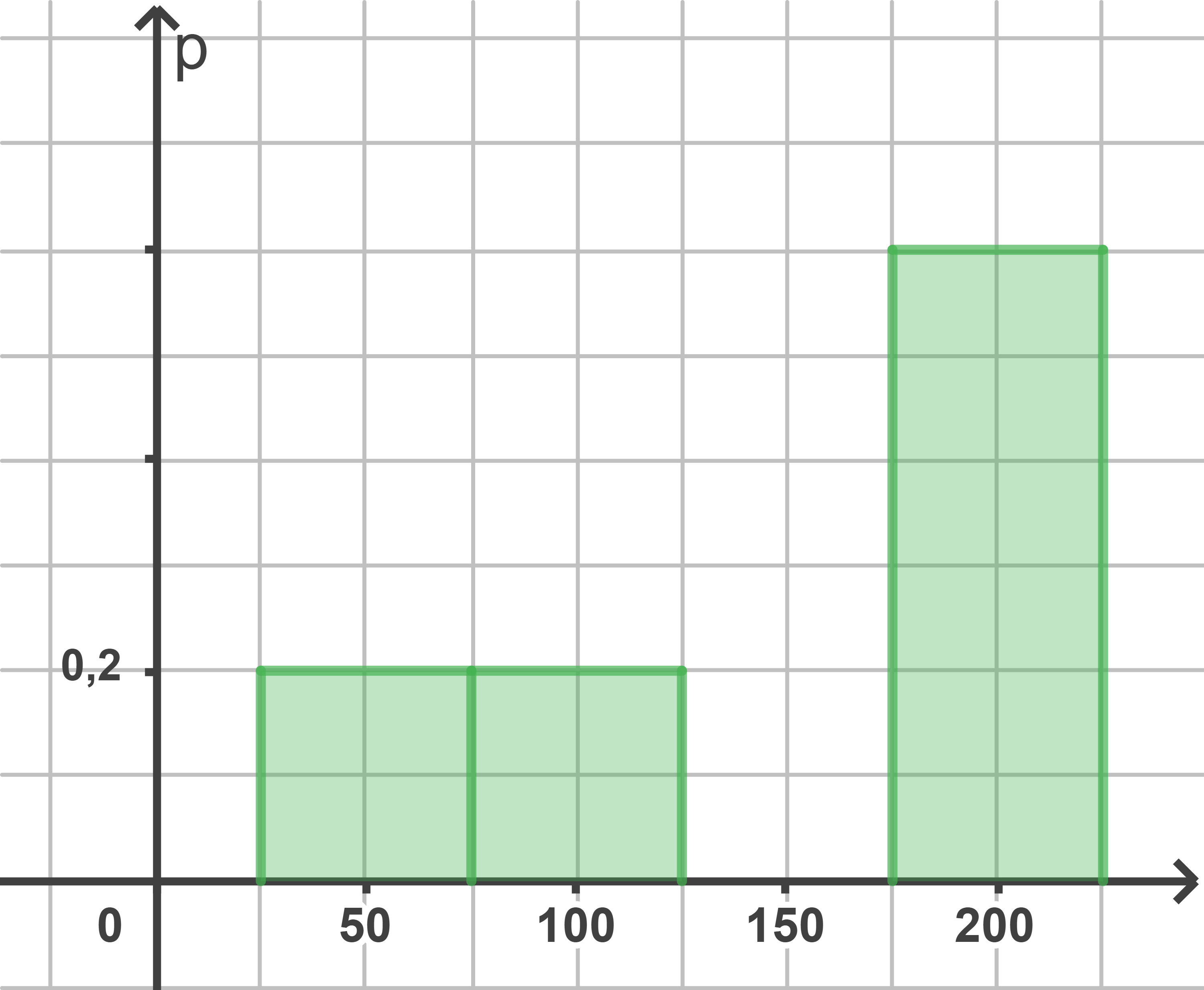
Für die Wahrscheinlichkeitsverteilung von
Eine der folgenden Abbildungen stellt diese Wahrscheinlichkeitsverteilung dar.
Abb. 1
Abb. 2
Abb. 3
4.1
Gib an und begründe, welche der Abbildungen diese Wahrscheinlichkeitsverteilung nicht darstellen.
(2 BE)
4.2
Ermittle den Erwartungswert von 
(3 BE)
1.1
1.2
Extremstellen berechnen:
1.Ableitung
Wende das notwendige Kriterium für Extremalstellen an, 
![\(\begin{array}[t]{rll}
0&=&3x^2-12x \\[5pt]
0&=&x \cdot (3x-12)\\[5pt]
x_1&=&0 \\[5pt]
x_2&=&4
\end{array}\)](https://mathjax.schullv.de/9cfa7952ac6e5f83e76d66e6fa22f2eb7b9579bb0efe3809ad10b1303b46ab30?color=5a5a5a)
2.Ableitung
Wende das hinreichende Kriterium für einen Hochpunkt an, 
1.3
Die Funktion 
hat die gleichen Extremstellen. Das bedeutet die Nullstellen der Ableitung sind gleich.
Da 
2.1
Es gilt:
Der Graph besitzt an einer Stelle den Anstieg 4: 
![\(\begin{array}[t]{rll}
f(x_0)+1 &=&4&\quad \scriptsize \mid\;-1 \\[5pt]
f(x_0)&=&3
\end{array}\)](https://mathjax.schullv.de/00494e8363e73562759466887f558ab4547cea6e68d28ad1b6027e553eb041e6?color=5a5a5a)
2.2
3.1
Für das Volumen gilt:
Es gilt: 
und
Es gilt: 
3.2
Mögliche Koordinaten:
4.1
Abb.1 nicht, da 
Abb.3 nicht, da:
Abb.3 nicht, da:
4.2
Erwartungswert:
Vollständige Lösung anzeigen