1 Analysis

1.1

Gib an, wie viele lokale Extrempunkte und wie viele Wendepunkte der Graph einer ganzrationalen Funktion vierten Grades höchstens haben kann.

(2 BE)

1.2

Gegeben ist eine reelle Funktion $g$ mit $g(x)=a \cdot x^4 + b \cdot x^3$ $+ c \cdot x^2 + d \cdot x + e,$ deren Graph $G$ folgende Eigenschaften besitzt:

$G$ verläuft durch die Punkte $O(0 \mid 0),$ $A\left( 5 \mid \frac{37}{8} \right)$ und $B(10 \mid 1).$
Im Punkt $A$ hat $G$ einen Anstieg von $m = -\frac{3}{2}.$
Die Tangente an $G$ im Punkt $B$ hat die Gleichung $y = \frac{2}{5}x - 3.$

Bestimme eine Gleichung der Funktion $g.$

(4 BE)

1.3

In einem Freizeitpark wird ein Abschnitt einer Achterbahn neu gebaut. Im Modell entspricht die $x$ -Achse des Koordinatensystems dem Erdboden. Die Höhe der Fahrbahn wird für alle $x$ im Intervall $[0;14]$ durch die Funktion $f$ mit

$f(x) = -\frac{1}{200}x^4 + \frac{41}{250}x^3 - \frac{7}{4}x^2 + \frac{31}{5}x + 1$

beschrieben. Die neu zu bauende Fahrbahn beginnt bei $f(0)$ und endet bei $f(14).$ Die Längeneinheit ist $10\;\text{m}.$ Ein Teil des Graphen von $f$ ist in Abbildung 2 dargestellt.

Abb. 1

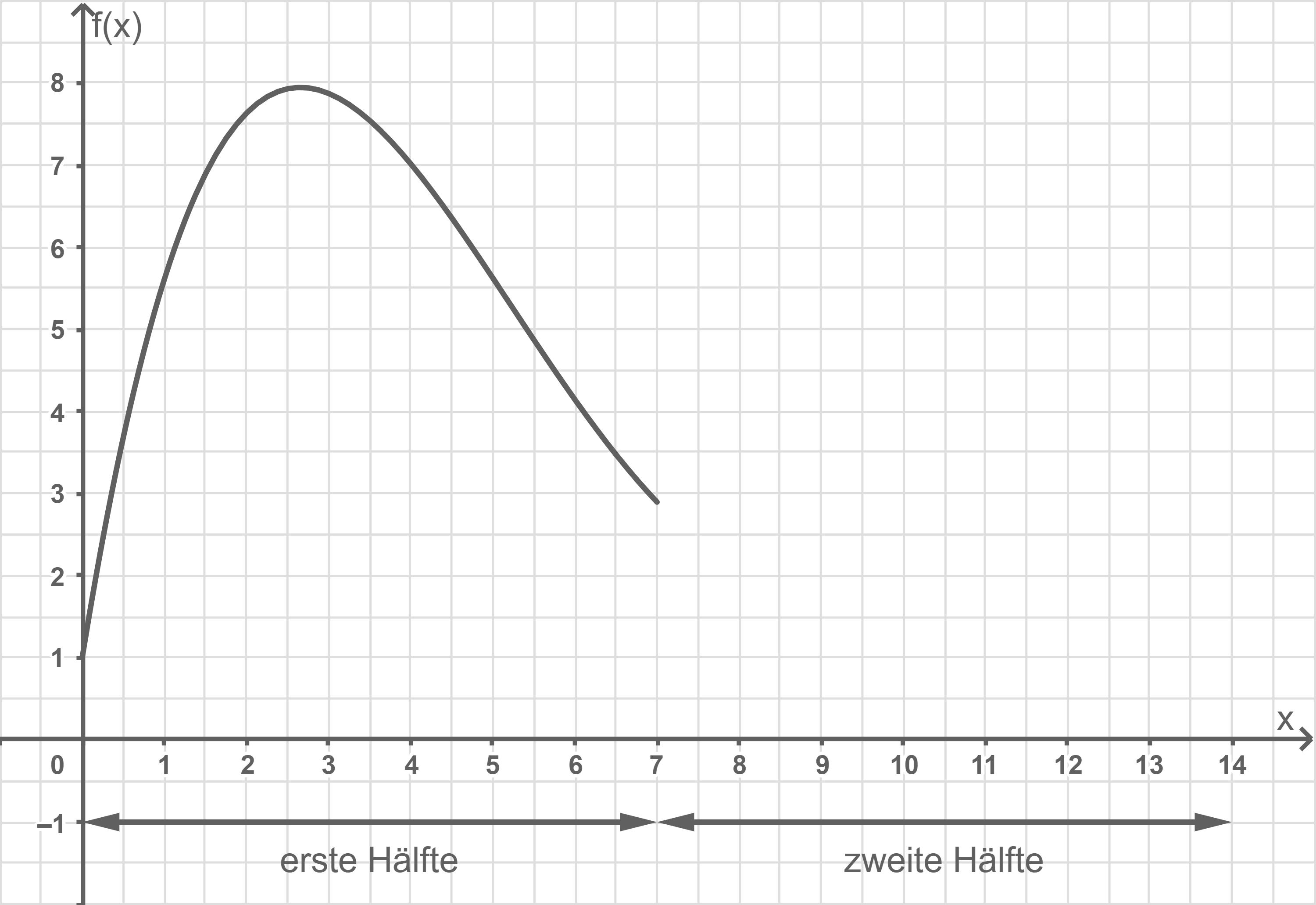
Abb. 2

1.3.1

Vervollständige den Graphen von $f$ in der Abbildung 2.

(2 BE)

1.3.2

Gib die größte Höhe der Fahrbahn in Metern an.

(2 BE)

1.3.3

Der Betreiber der Achterbahn behauptet, dass schon die erste Abfahrt eine Neigung von über $50^\circ$ erreicht.

Überprüfe diese Behauptung rechnerisch.

(4 BE)

1.3.4

In der ersten Hälfte des neu zu bauenden Abschnitts ändert sich nur die Höhe der Achterbahn, es gibt demnach keine Links- oder Rechtskurven. Hier soll für spätere Lichtshows eine gerade Strebe angebaut werden. Die Strebe ist $22\;\text{m}$ lang, soll horizontal verlaufen und wird in ihren Endpunkten seitlich an der Fahrbahn befestigt.

Bestimme die Koordinaten der Befestigungspunkte im Modell.

(4 BE)

1.3.5

Der neu zu bauende Abschnitt soll am Ende nahtlos an die bereits bestehende Achterbahn angebunden werden. Der Höhenverlauf der Fahrbahn im anschließenden Abschnitt wird durch den Graphen einer anderen Funktion $q$ beschrieben.

Erläutere im Sachzusammenhang zwei Eigenschaften, die die Funktionen $f$ und $q$ an der Stelle $x = 14$ dafür gemeinsam haben müssen.

(4 BE)

1.4

An einer beliebten, bereits bestehenden Achterbahn bildet sich stets eine Warteschlange. Für einen bestimmten Tag wird die Anzahl der wartenden Besucher durch die reelle Funktion $w$ mit $w(t) = 1500 \cdot \left( \mathrm{e}^{-0,2 \cdot t} - \mathrm{e}^{-0,8 \cdot t} \right)$ modelliert. Dabei ist $t$ die Zeit in Stunden im Zeitraum von $10:00$ bis $19:30$ Uhr und $t = 0$ entspricht $10:00$ Uhr.

1.4.1

Vergleiche die Anzahl der wartenden Besucher um $11:00$ Uhr und um $14:30$ Uhr.

Bestimme eine Uhrzeit, zu der 350 Besucher warten.

(6 BE)

1.4.2

Bestimme rechnerisch, wie viele Stunden nach Öffnung des Parks um $10:00$ Uhr die meisten Besucher warten.

(3 BE)

1.4.3

Aus Erfahrung heraus wissen die Betreiber des Freizeitparks, dass wartende Besucher durchschnittlich $15\;\text{g}$ Müll pro Person und Stunde hinterlassen.

Berechne $\displaystyle\int_{0}^{8}0,015\cdot w(t)\;\mathrm {dt}.$

Interpretiere das Ergebnis im Sachzusammenhang.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Eine ganzrationale Funktion vierten Grades kann höchstens drei lokale Extrempunkte und zwei Wendepunkte haben.

1.2

Die erste Eigenschaft liefert $g(0)=0,$ $g(5)=\frac{37}{8}$ und $g(10)=1.$ Durch die zweite Eigenschaft folgt $\(g$ und die dritte Eigenschaft liefert $\(g$ Für die erste Ableitung der Funktion $g$ gilt:

$\(g$

Aus $g(0)=0$ folgt direkt $e=0,$ das heißt aus den restlichen Gleichungen ergibt sich das folgende lineare Gleichungssystem:

Gleichungssystem anzeigen

Lösen dieses Gleichungssystems mit dem CAS liefert folgende Werte:

$\begin{array}[t]{rll} a&=&-\dfrac{1}{200} \\[5pt] b&=&\dfrac{41}{250} \\[5pt] c&=&-\dfrac{7}{4} \\[5pt] d&=&\dfrac{31}{5} \end{array}$

Somit ergibt sich die Gleichung $g(x)=-\frac{1}{200} x^4+\frac{41}{250} x^3$ $-\frac{7}{4} x^2+\frac{31}{5} x$ für $g.$

1.3

1.3.1

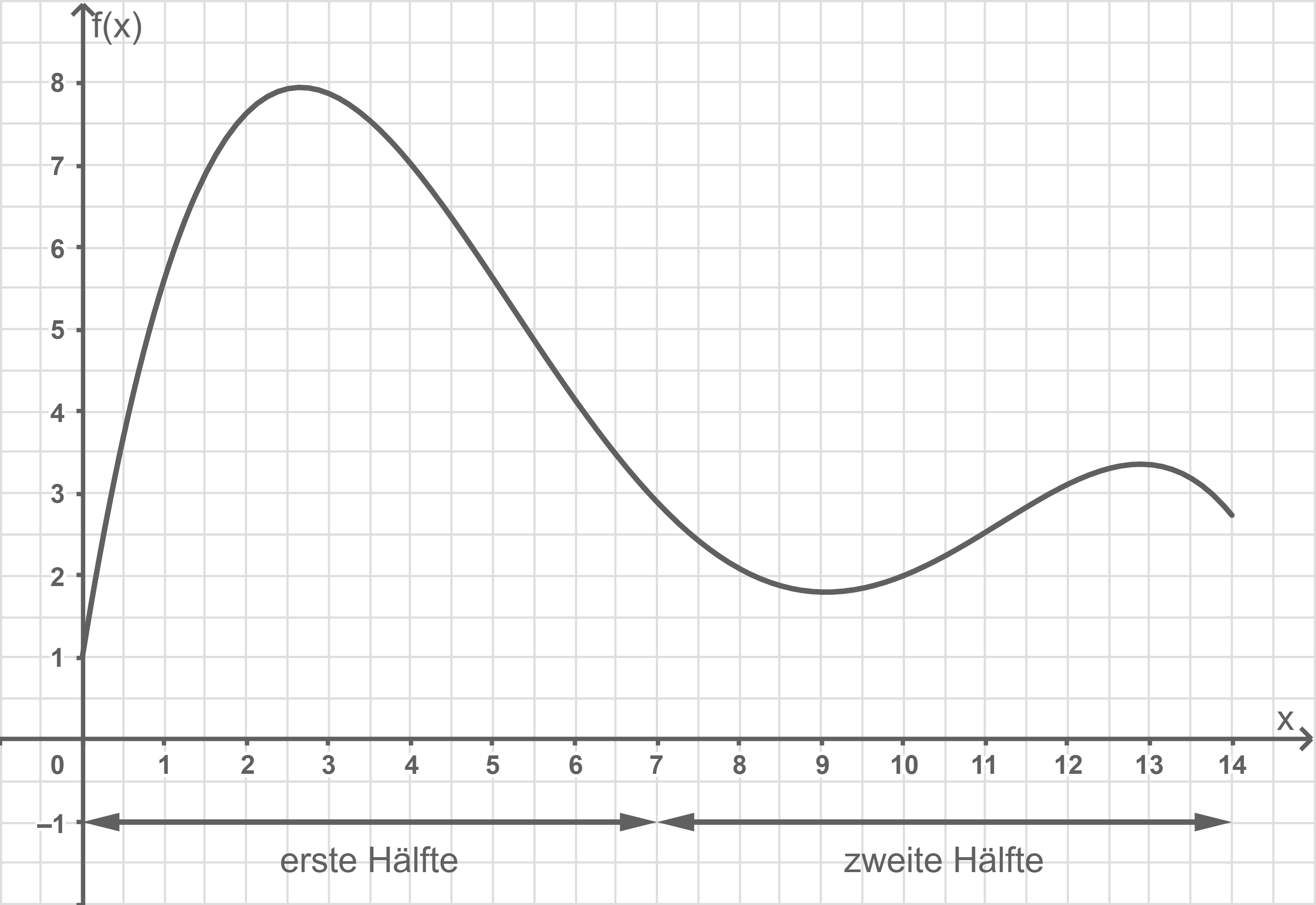
1.3.2

Die größte Höhe der Fahrbahn entspricht dem Maximum der Funktion $f(x).$ Graphische Bestimmung im CAS liefert, dass der maximale Wert 8 beträgt. Da eine Längeneinheit $10\;\text{m}$ entspricht, folgt somit, dass die größte Höhe der Fahrbahn $8\cdot10=80\;\text{m}$ beträgt.

1.3.3

Mit dem CAS folgt für die ersten beiden Ableitungen von $f:$

$\(f$ $-\dfrac{7}{2}x+\dfrac{31}{5}$

$\(f$

Die Stellen von den Abfahrten mit maximaler Neigung sind durch die Wendestellen von $f$ gegeben. Lösen von $\(f$ im CAS mit dem solve-Befehl liefert:

$\begin{array}[t]{rll} x_1&\approx&5,22 \\[5pt] x_2&\approx&11,18 \end{array}$

Der Wert $x_2$ kann hierbei vernachlässigt werden, da $x_1$ zur ersten Abfahrt gehört. Für den gesuchten Neigungswinkel $\alpha$ ergibt sich somit die folgende Gleichung:

Gleichung anzeigen

Mit dem solve-Befehl des CAS folgt $\alpha\approx-56,5^\circ.$ Somit stimmt die Behauptung.

1.3.4

Die Strebe ist 22 Meter lang und verläuft horizontal, das heißt es ist der Wert von $x$ mit $f(x+2,2)=f(x)$ gesucht. Mit dem solve-Befehl des CAS ergibt sich:

$\begin{array}[t]{rll} x_1&\approx&1,66 \\[5pt] x_2&\approx&8,00 \\[5pt] x_3&\approx&11,64 \end{array}$

Da die Strebe in der ersten Hälfte angebaut werden soll, ist der gesuchte Wert $x_1\approx1,66.$ Es ergibt sich $1,66+2,2=3,86.$ Einsetzen von $x_1$ in $f(x)$ liefert:

Rechenweg anzeigen

$f(1,66) \approx 7,18$

Damit ergeben sich die gesuchten Koordinaten der beiden Befestigungspunkte durch $(1,66\mid7,18)$ und $(3,86\mid7,18).$

1.3.5

Um sicherzustellen, dass der neu zu bauende Abschnitt nahtlos an die bestehende Achterbahn angebunden wird, müssen die Funktionen ohne Unterbrechung und ohne Knick ineinander übergehen. Somit muss $f(14) = q(14)$ und $\(f$ gelten.

1.4

1.4.1

Wartende Besucher vergleichen

$\begin{array}[t]{rll} w(1)&=&1500 \cdot \left( \mathrm{e}^{-0,2 \cdot 1} - \mathrm{e}^{-0,8 \cdot 1} \right) \\[5pt] &\approx&554 \end{array}$

$\begin{array}[t]{rll} w(4,5)&=&1500 \cdot \left( \mathrm{e}^{-0,2 \cdot 4,5} - \mathrm{e}^{-0,8 \cdot 4,5} \right) \\[5pt] &\approx&569 \end{array}$

Somit warten um $14:30$ Uhr ca. $569-554=15$ Besucher mehr als um $11:00$ Uhr.

Uhrzeit bestimmen

Auflösen von $w(t) = 350$ mit dem CAS liefert:

$\begin{array}[t]{rll} t_1&\approx&0,5 \\[5pt] t_2&\approx&7,21 \end{array}$

Es warten somit z.B. gegen $10:30$ Uhr $350$ Besucher.

1.4.2

Mit dem CAS folgt für die ersten beiden Ableitungen von $w:$

$\(w$ $\cdot \left( -0,2 \mathrm{e}^{-0,2t} + 0,8 \mathrm{e}^{-0,8t} \right)$

$\(w$ $\cdot \left( 0,04 \mathrm{e}^{-0,2t} - 0,64 \mathrm{e}^{-0,8t} \right)$

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

Auflösen von $\(w$ nach $t$ mit dem solve-Befehl des CAS liefert $t\approx2,31.$

2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen

Einsetzen von $t\approx2,31$ in $\(w$ liefert:

Rechenweg anzeigen

$\(w$

Somit besitzt $w$ an der Stelle $t\approx2,31$ ein lokales Maximum, das heißt ungefähr $2,31$ Stunden nach Öffnung des Parks (etwa um 12:18 Uhr) warten die meisten Besucher.

1.4.3

Mit dem CAS folgt:

Rechenweg anzeigen

$\displaystyle\int_{0}^{8}0,015\cdot w(t)\;\mathrm dt\approx 61,71$

An der Achterbahn beträgt somit die Menge des Mülls von $10:00$ Uhr bis $18:00$ Uhr ca. $61,71\;\text{kg}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?