Analytische Geometrie

Die Eckpunkte eines ebenen, dreieckigen Sonnensegels können in einem Koordinatensystem durch die Punkte $A(5\mid 0\mid 5),$ $B(0\mid 4\mid 4),$ und $C(5\mid 4\mid 2)$ beschrieben werden. Im verwendeten Koordinatensystem stellt die $xy$ -Ebene den horizontalen Untergrund dar. Eine Längeneinheit entspricht $1\text{m}$ .

3.1

Das Sonnensegel soll für eine abendliche Veranstaltung mit einer Lichterkette entlang seiner Kanten versehen werden.

Berechne die Mindestlänge der Lichterkette.

(3 BE)

3.2

Es gibt eine Ebene $E,$ in der die Punkte $A,$ $B$ und $C$ liegen. Ermittle eine Gleichung von $E$ in Koordinatenform.

Zur Kontrolle: $\overrightarrow{n_E}=\pmatrix{8\\15\\20}$

(3 BE)

3.3

Berechne die Größe des Neigungswinkels des Sonnensegels zum Erdboden.

(2 BE)

3.4

An einem Sommertag treffen die Sonnenstrahlen senkrecht auf das Sonnensegel.

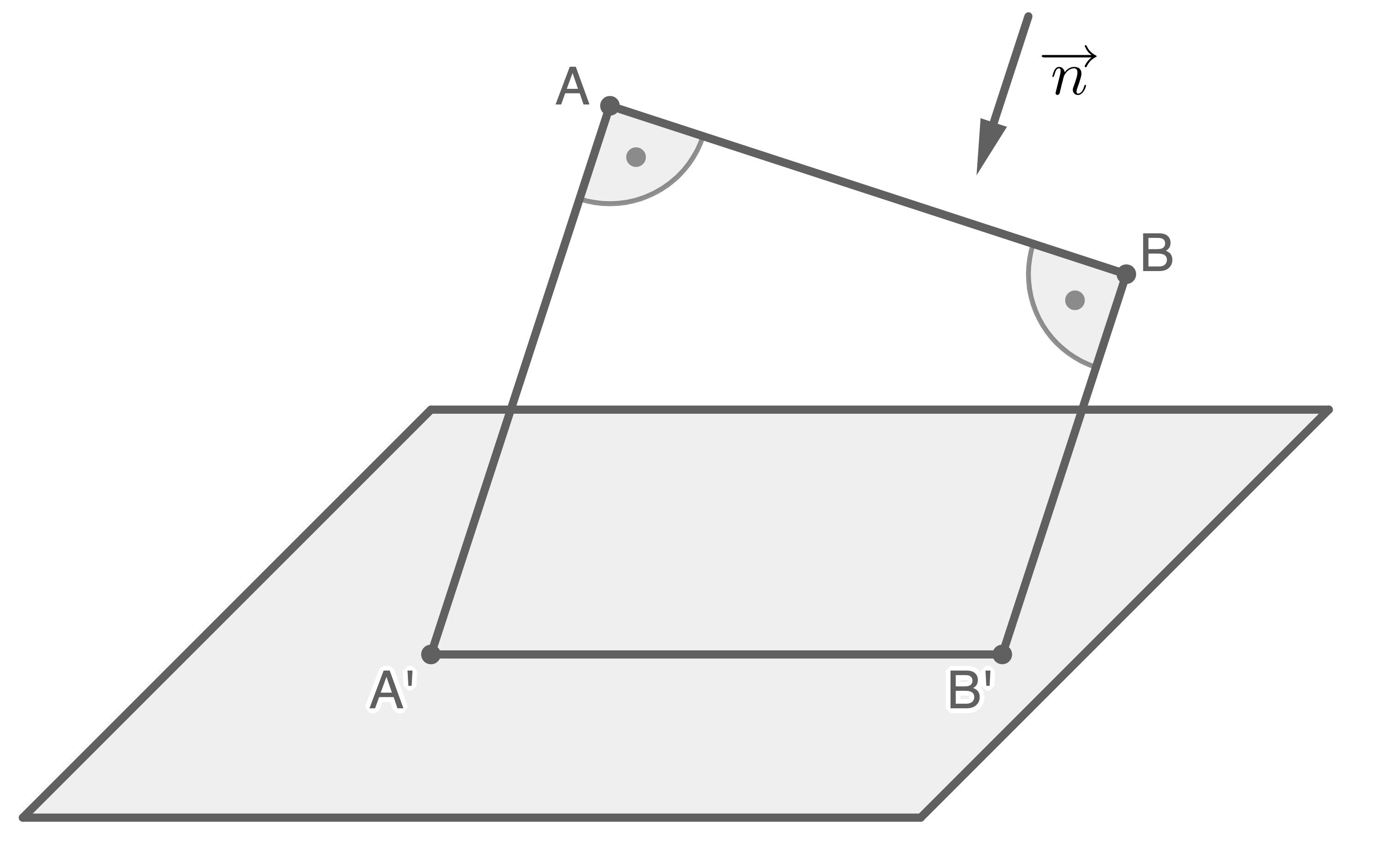
Begründe mithilfe einer Skizze, dass dabei die Länge des Schattens einer beliebigen Kante des Sonnensegels nicht kleiner sein kann als die Länge der Kante selbst.

(2 BE)

Betrachtet wird der Stumpf $ABCDEFGH$ der schiefen Pyramide $ABCDS.$ Die Grundfläche $ABCD$ mit $A(4\mid 0\mid 0),$ $B(4\mid 4\mid 0),$ $C(0\mid 4\mid 0)$ und $D(0\mid 0\mid 0)$ sowie die Deckfläche des Stumpfs mit $E(3\mid 0\mid 4),$ $F(3\mid 3\mid 4),$ $G(0\mid 3\mid 4)$ und $H(0\mid 0\mid 4)$ sind quadratisch.

4.1

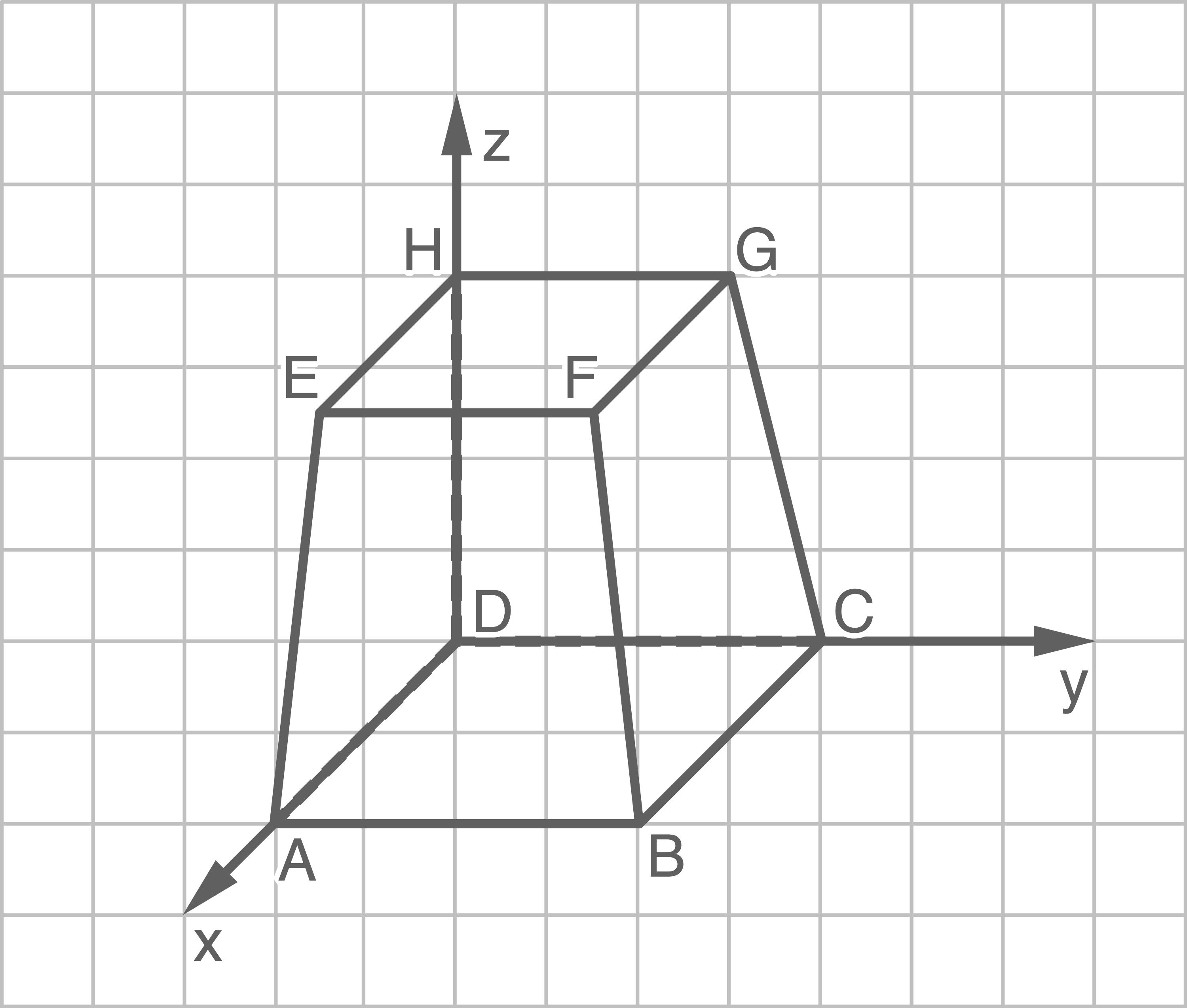
Zeichne den Stumpf in ein dreidimensionales Koordinatensystem ein.

(3 BE)

4.2

Erläutere das folgende Vorgehen zur Bestimmung der $z$ -Koordinate der Pyramidenspitze $S.$

Aus $\pmatrix{4\\0\\0}+r\cdot \pmatrix{-1\\0\\4}=\pmatrix{0\\0\\k}$ ergibt sich $k=16.$

(3 BE)

4.3

Bestimme das Volumen des Stumps.

(3 BE)

$\,$

Der Mittelpunkt $M$ der Kante $\overline{AB}$ und der Mittelpunkt $N$ der Kante $\overline{CG}$ liegen auf der Gerade

$j:\overrightarrow{x}=\pmatrix{4\\2\\0}+s\pmatrix{-8\\3\\4}$ mit $s\in\mathbb{R}.$

4.4

Bestimme die Koordinaten des Schnittpunkts von $j$ mit der $xz$ -Ebene.

(3 BE)

4.5

Die Punkte der Kante $\overline{BC}$ lassen sich in der Form $P_w(w\mid 4\mid 0)$ darstellen.

4.5.1

Für einen Punkt $P_w$ der Kante $\overline{BC}$ schneidet die Gerade durch $H$ und $P_w$ die Gerade $j.$
Berechne den zugehörigen Wert von $w.$

(3 BE)

4.5.2

Es gibt Punkte $P_w$ der Kante $\overline{BC},$ für die der von den Strecken $\overline{P_wM}$ und $\overline{P_wH}$ eingeschlossende Winkel größer als $70^\circ$ ist. Ermittle die zugehörigen Werte von $w.$

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

Die Mindestlänge entspricht dem Umfang des Dreiecks $ABC.$

$U=|\overrightarrow{AB}|+|\overrightarrow{BC}|+|\overrightarrow{CA}|$ $=\left|\left(\begin{array}{c} -5 \\ 4 \\ -1 \end{array}\right)\right|+\left|\left(\begin{array}{c} 5 \\ 0 \\ -2 \end{array}\right)\right|+\left|\left(\begin{array}{c} 0 \\ -4 \\ 3 \end{array}\right)\right|$ $\approx 16,9$

Die Mindestlänge der Lichterkette beträgt 16,9 m.

3.2

Für die Ebene wird eine Parametergleichung $\overrightarrow{x}=\overrightarrow{OA}+r \cdot \overrightarrow{AB}+s \cdot \overrightarrow{AC}$ bzw. $\left(\begin{array}{l}x \\ y \\ z\end{array}\right)=\left(\begin{array}{l}5 \\ 0 \\ 5\end{array}\right)+r \cdot\left(\begin{array}{c}-5 \\ 4 \\ -1\end{array}\right)+s \cdot\left(\begin{array}{c}0 \\ 4 \\ -3\end{array}\right)$ aufgestellt und mit dem CAS nach den Parametern $r$ , $s$ und $x$ gelöst. Daraus ergibt sich $x=\dfrac{-15 y-20 z+140}{8}$ .

Durch Umstellen erhält man $E: 8 x+15 y+20 z=140$ .

Alternative Lösung

Die Koordinatenform der Ebenengleichung von $E$ lautet mit $P(x|y| z):$

$E(P)=a x+b y+c z$ $=\overrightarrow{O P} \circ\left(\begin{array}{l}a \\ b \\ c\end{array}\right)=d$ mit unbekannten Werten von $a, b, c$ und $d$ . Das Einsetzen von $A, B$ und $C$ liefert mit $d=1$ ein Gleichungssystem, dessen Lösung gemäß CAS lautet:

$a=\dfrac{2}{35}, b=\dfrac{3}{28}, c=\dfrac{1}{7}$

Eine Ebenengleichung in Koordinatenform lautet:

$E: \dfrac{2}{35} x+\dfrac{3}{28} y+\dfrac{1}{7} z=1$ bzw. $E: 8 x+15 y+20 z=140$

3.3

Zu berechnen ist ein Schnittwinkel zwischen zwei Ebenen.

$\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)$ ist ein Normalenvektor der $xy$ -Ebene, $\left(\begin{array}{c}8 \\ 15 \\ 20\end{array}\right)$ Normalenvektor von $E.$

$\varphi=\arccos \left(\frac{\left(\begin{array}{c}8 \\ 15 \\ 20\end{array}\right) \circ\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)}{\left|\left(\begin{array}{c}8 \\ 15 \\ 20\end{array}\right)\right| \cdot\left|\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right)\right|}\right) \approx 40,4^{\circ}$

Der Neigungswinkel beträgt etwa 40 Grad.

3.4

Zwei Eckpunkte des Segels bilden mit ihren zugehörigen Schattenpunkten ein rechtwinkliges Trapez, da die Sonnenstrahlen senkrecht auf das Sonnensegel treffen.

Verläuft $\overline{AB}$ parallel zum Erdboden, dann gilt $\left|\overline{A^{\prime} B^{\prime}}\right|=|\overline{AB}|$ .

Verläuft $\overline{AB}$ schräg zum Erdboden, dann gilt $\left|\overline{A^{\prime} B^{\prime}}\right|>|\overline{AB}|$ .

Somit kann die Schattenlänge nicht kleiner als die Kantenlänge sein.

4.1

Mecklenburg-Vorpommern Abi 2022 Pyramidenstumpf

4.2

Die Gerade mit der Gleichung $\vec{x}=\left(\begin{array}{l}4 \\ 0 \\ 0\end{array}\right)+r \cdot\left(\begin{array}{c}-1 \\ 0 \\ 4\end{array}\right)$ verläuft durch $A$ und $E.$

$S$ liegt auf der Verlängerung der Kante $\overline{DH}$ . Da die Punkte $D$ und $H$ auf der $z$ -Achse liegen, gilt dies auch für $S.$

$S$ hat demzufolge die Koordinaten $S(0|0| k)$ .

Da $S$ auch auf der Verlängerung der Kante $\overline{AE}$ liegt, lässt sich der $z$ -Wert $k$ von $S$ durch Lösen der angegebenen Gleichung ermitteln.

4.3

Grund- und Deckfläche sind quadratisch:

$A_{G}=(|\overrightarrow{AB}|)^{2}=16$ und $A_{D}=(|\overrightarrow{EF}|)^{2}=9$

$V=\dfrac{1}{3} \cdot h \cdot\left(A_{G}+\sqrt{A_{G} \cdot A_{D}}+A_{D}\right)$ $=\dfrac{1}{3} \cdot 4 \cdot(16+\sqrt{16 \cdot 9}+9)=\dfrac{148}{3}$

4.4

Gesucht ist der Punkt auf der Geraden $j,$ dessen $y$ -Koordinate 0 ist: $\left(\begin{array}{l} x\\0\\z \end{array}\right)=\left(\begin{array}{l} 4 \\ 2 \\ 0 \end{array}\right)+s \cdot\left(\begin{array}{c} -8 \\ 3 \\ 4 \end{array}\right)$

$x=\dfrac{28}{3},$ $z=-\dfrac{8}{3},$ $s=-\dfrac{2}{3}$

Der Schnittpunkt hat die Koordinaten $\left(\dfrac{28}{3}\bigg\vert 0\bigg\vert -\dfrac{8}{3}\right)$ .

4.5.1

Für die Gerade $k$ durch $H$ und $P_{w}$ erhält man:

$k:\overrightarrow{x}=\overrightarrow{OH}+t\cdot \overrightarrow{HP_{w}}$ $=\left(\begin{array}{l}0 \\ 0 \\ 4\end{array}\right)+t \cdot\left(\begin{array}{c}w \\ 4 \\ -4\end{array}\right)$ mit $\mathrm{t} \in \mathbb{R}$

Gleichsetzen der Terme beider Geraden und Lösen der Gleichung

$\left(\begin{array}{l} 4 \\ 2 \\ 0 \end{array}\right)+s \cdot\left(\begin{array}{c} -8 \\ 3 \\ 4 \end{array}\right)=\left(\begin{array}{l} 0 \\ 0 \\ 4 \end{array}\right)+t \cdot\left(\begin{array}{c} w \\ 4 \\ -4 \end{array}\right)$ liefert $w=\dfrac{12}{5}$ für den Schnittpunkt von $k$ und $j$ .

4.5.2

$M(4|2| 0)$ ist Mittelpunkt der Kante $\overline{AB}$ .

$\overrightarrow{P_{w} M}=\left(\begin{array}{c} 4-w \\ -2 \\ 0 \end{array}\right)$ , $\overrightarrow{P_{w} H}=\left(\begin{array}{c} -w \\ -4 \\ 4 \end{array}\right)$

Die Größe $\varphi$ des eingeschlossenen Winkels kann in Abhängigkeit von $w$ mit Hilfe des Terms arccos $\left(\dfrac{\overrightarrow{P_{w} M} \circ \overline{P_{w} H}}{\left|\overrightarrow{P_{w} M}\right| \cdot\left|P_{w} H\right|}\right)$ berechnet werden.

Die Gleichung arccos $\left(\dfrac{\overrightarrow{P_{w} M} \circ \overrightarrow{P_{w} H}}{\left|\overrightarrow{P_{w} M}\right| \cdot\left|P_{w} H\right|}\right)=70^{\circ}$ hat die zwei Lösungen $w_{1} \approx-0,26$ und $w_{2} \approx 2,96.$

Da $P_{w}$ auf der Kante $\overline{B C}$ liegt, gilt $0 \leq w \leq 4$ , also entfällt die Lösung $\mathrm{w}_{1}$ .

Entspricht $P_{w}$ dem Punkt $B$ , so gilt: $w=0$ mit $\varphi \approx 71,6^{\circ}$ .

Bewegt sich der Punkt $P_{w}$ in Richtung des Punktes $C$ , so strebt $w$ gegen den Wert 4 und der Winkel wird stetig kleiner. Somit ist für $0 \leq w\lt w_{2}$ ist der betrachtete Winkel größer als $70^{\circ}$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?