Wahlteil A2
A2 Analytische Geometrie
Gegeben sind in einem kartesischen Koordinatensystem die Punkte
2.1
Ermittle eine Koordinatengleichung der Ebene  , in der die Punkte
, in der die Punkte  ,
,  und
und  liegen.
liegen.
Berechne die Koordinaten des Durchstoßpunktes der -Achse durch
-Achse durch  .
.
Weise nach, dass der Punkt mit den Koordinaten
mit den Koordinaten  in
in  liegt.
liegt.
Berechne die Koordinaten des Durchstoßpunktes der
Weise nach, dass der Punkt
2.2
Die Punkte  ,
,  ,
,  und
und  bilden die Grundfläche einer Pyramide
bilden die Grundfläche einer Pyramide  mit der Spitze
mit der Spitze  .
.
2.2.1
Untersuche, ob  ein Parallelogramm ist.
ein Parallelogramm ist.
2.2.2
Stelle die Pyramide grafisch dar.
2.2.3
Bestimme rechnerisch die Höhe  der Pyramide und die Größe des Winkels, der von den Seitenkanten
der Pyramide und die Größe des Winkels, der von den Seitenkanten  und
und  eingeschlossen wird.
eingeschlossen wird.
2.2.4
Berechne das Volumen der Pyramide.
2.3
Gegeben sind weiterhin die Punkte  mit
mit  .
.
2.3.1
Bestimme den Wert von  so, dass die Vektoren
so, dass die Vektoren  und
und  orthogonal sind.
orthogonal sind.
2.3.2
Berechne für jedes der Dreiecke  den Flächeninhalt in Abhängigkeit von
den Flächeninhalt in Abhängigkeit von  .
Für einen Wert von
.
Für einen Wert von  ist dieser Flächeninhalt minimal. Berechne für diesen Wert den Flächeninnhalt.
ist dieser Flächeninhalt minimal. Berechne für diesen Wert den Flächeninnhalt.
2.3.3
Bestimme alle Werte von  , für die die folgende Aussage gilt:
, für die die folgende Aussage gilt:
Der Punkt liegt in der jeweiligen Ebene
liegt in der jeweiligen Ebene  .
.
Der Punkt
A2 Analytische Geometrie
2.1
- Bestimme einen Normalenvektor der Ebene mit dem Kreuzprodukt zweier Vektoren, die in der Ebene liegen. Verwende zwei Verbindungsvektoren der drei Punkte, die in der Ebene liegen sollen.
- Den Parameter
kannst du dann bestimmen, indem du die Koordinaten eines Punkts in die Ebenengleichung einsetzt.
 Abb. 1: Kreuzprodukt
Abb. 1: Kreuzprodukt
2.2.1
- Die Eckpunkte
und
liegen nebeneinander. In dem Fall liegt der Seite
die Seite
gegenüber.
- Die Eckpunkte
und
liegen sich gegenüber. In dem Fall liegt die Seite
der Seite
gegenüber.
Die Seiten
2.2.2
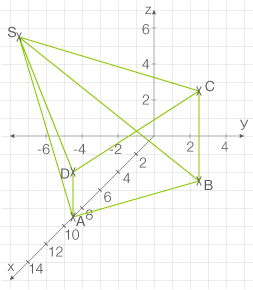 Abb. 2: Pyramide
Abb. 2: Pyramide
2.2.3
2.2.4
A2 Analytische Geometrie
2.1
- Bestimme einen Normalenvektor der Ebene mit dem Kreuzprodukt zweier Vektoren, die in der Ebene liegen. Verwende zwei Verbindungsvektoren der drei Punkte, die in der Ebene liegen sollen.
- Den Parameter
kannst du dann bestimmen, indem du die Koordinaten eines Punkts in die Ebenengleichung einsetzt.
 Abb. 1: Kreuzprodukt
Abb. 1: Kreuzprodukt
2.2.1
- Die Eckpunkte
und
liegen nebeneinander. In dem Fall liegt der Seite
die Seite
gegenüber.
- Die Eckpunkte
und
liegen sich gegenüber. In dem Fall liegt die Seite
der Seite
gegenüber.
Die Seiten
2.2.2
 Abb. 2: Pyramide
Abb. 2: Pyramide
2.2.3
2.2.4
2.3.1
2.3.2
- Notwendiges Kriterium:
- Hinreichendes Kriterium: Ist
, handelt es sich um eine Minimalstelle.
- Bestimme die ersten beiden Ableitungsfunktionen
und
.
- Wende das notwendige Kriterium an, indem du
setzt und nach
löst.
- Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in
einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
- Berechne die Funktionswerte von
an der Minimalstelle. Dies ist dann der gesuchte minimale Flächeninhalt.
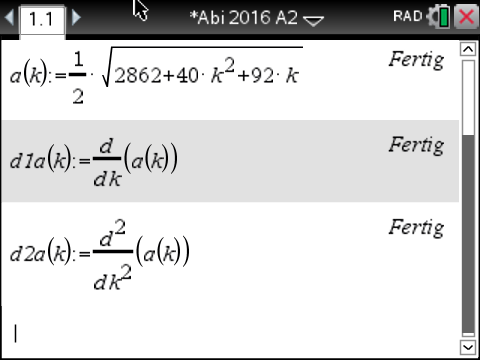
Du kannst dein CAS nutzen. Definiere dazu zunächst die Funktion  und anschließend die ersten beiden Ableitungen. Den Befehl für eine Ableitung findest du unter
und anschließend die ersten beiden Ableitungen. Den Befehl für eine Ableitung findest du unter
keyboard  Math2
Math2
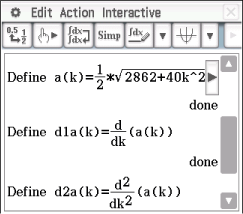 Abb. 3: Ableitungen definieren
Abb. 3: Ableitungen definieren
Durch Gleichsetzen von  mit Null, erhältst du mögliche Extremstellen. Die Gleichung kannst du mit dem solve-Befehl deines CAS lösen.
mit Null, erhältst du mögliche Extremstellen. Die Gleichung kannst du mit dem solve-Befehl deines CAS lösen.

 Abb. 4: Notwendiges Kriterium
Abb. 4: Notwendiges Kriterium
Überprüfe nun mit dem hinreichenden Kriterium, ob es sich tatsächlich um ein Minimum handelt. Berechne dazu  mit deinem CAS:
mit deinem CAS:

 Es handelt sich also tatsächlich um eine Minimalstelle.
Es handelt sich also tatsächlich um eine Minimalstelle.
 Abb. 5: Hinreichendes Kriterium
Abb. 5: Hinreichendes Kriterium
2.3.3
© 2017 - SchulLV.